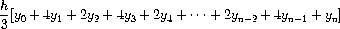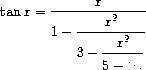Bonus Question 2 -- 2 points
A string is a collection of characters surrounded by double quotes. An
example of a string is "hello". For this problem you should write
the procedure string-to-frequency-list. This procedure
should take in a string, and return a list of symbol-frequency
pairs. An example of symbol-frequency pair is the list (#\h
2). #\h is the symbol (remember #\h
is a character, not an actual scheme symbol), and 1 is the frequency, or
the number of times #\h appeared in some string we wanted
to encode. str2frequency-list must return a list of
these frequency pairs, one pair for each unique character in the
string passed to string-to-frequency-list.
(string-to-frequency-list "hello") should return the list:
((#\h 1) (#\e 1) (#\l 2) (#\o 1)), or a similar list with
a different ordering of the symbol-frequency pairs.
The procedure string->list is built into STk, and may be
useful to you. It takes in a string and returns the list containing
each of the characters in the string in the order they appear in the
string. So for instance (string->list "hello") would return
the list (#\h #\e #\l #\l #\o).
string-to-frequency-list is more complicated
than procedures in prior labs. Plan how to decompose the problem into
simpler problems before you start writing your procedure.
You can come up with your own solution, or follow the steps outlined here:
- Write a procedure
(unique L) which will examine a
list and return a sublist with all duplicates removed. For example
(unique (list 3 1 3 4 1)) would return a list like
(3 1 4) which has the duplicate elements removed.
Tip: You can
use (member x lst) to check if x is list
lst.
- Write a procedure
(count-occurrences obj L) which
will count the number of times obj appears in the list
L.
Tip:
To test if two numbers are the same you have seen
the = operator, but this only works for numbers. To test
if x and y are the same for more general
kinds of data you can use (eqv? x y).
- Go over the list of unique characters
(generated with the
unique and string->list
functions.) Ideally you you will use the map function to
recurse over this list.
Use count-occurences to generate the frequencies
for each unique character during your recursive or iterative process.
Useful procedures for the bonus question:
-
(member obj lst) returns a
nonfalse value if obj is found in list lst or
#f otherwise. More precisely, if obj is
in the list lst it will return the list starting at
obj.
(eqv? obj1 obj2) returns
#t if obj1 and obj2 are the same.
It works for numbers, characters, and symbols, but not for lists.
To compare characters you can also use (char=? char1 char2)
-
(string->list str)
returns a list of characters contained in string str.