Evaluate the following expressions in sequence and write the value they return after the =>.
(define b (- 22 7)) | |
(- 21 b) | => |
(define (foo x y) (- (+ x y) 2)) | |
(/ b (foo 2 3)) | => |
(foo b 5) | => |
((if (> (foo 2 3) b) + *) 4 3) | => |
(+ (if (and (odd? b) (> b 10)) 1 0) b) | => |
(foo (foo 1 2) 3) | => |
(foo (foo (foo 1 2) 3) (foo 4 5)) | => |
(cond ((<= b 0) 0)
((> b 10) (/ b 10))
(else b))
| => |
Write a procedure (add-sq-odd n) to add the square of the odd integers from 0 to n. Assume n is a positive integer. It should work like this:
STk> (define (square x) (* x x)) square STk> (add-sq-odd 6) 35 ; since 1+(3*3)+(5*5)=35 STk> (add-sq-odd 5) 35 ; since 1+(3*3)+(5*5)=35 STk> (add-sq-odd 3) 10 ; since 1+(3*3)=10State whether your procedure generates a linear iterative or a linear recursive process.
Write a procedure to count how many integers are multiple of 3 in a given range (extremes included). It should work like this:
STk> (count-multipleof3 1 9) 3 STk> (count-multipleof3 9 9) 1 STk> (count-multipleof3 7 8) 0Does your procedure generate a linear iterative process or a linear recursive process?
The value of the number
e, a transcendental number
which is used as the base for natural logarithms, can be computed
as the sum of the infinite series 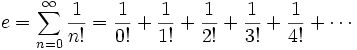
Write a procedure
(compute-e n) to compute the
value of e using the first n terms
of the series. It should work like this:
STk> (compute-e 16) 2.71828182845904 STk> (compute-e 20) 2.71828182845905
[This is part of exercise 1.23 on page 54 of the textbook.] Rewrite the procedure
find-divisor so that the values used for
test-divisor are 2, 3, 5, 7, 9, .. instead of
2, 3, 4, 5, 6, 7, 8, 9, .. To make this change, define a procedure
next that returns
3 if its input is 2 and otherwise returns its input plus 2.Modify
find-divisor to use (next test-divisor)
instead of (+ test-divisor 1).
(define (smallest-divisor n) (find-divisor n 2)) (define (find-divisor n test-divisor) (cond ((> (square test-divisor) n) n) ((divides? test-divisor n) test-divisor) (else (find-divisor n (+ test-divisor 1))))) (define (divides? a b) (= (remainder b a) 0))How much faster do you expect the new version of
find-divisor
to be?
Write a predicate (ever-negative? f n) that returns #t if the procedure f is negative on any of the integers in the range 0 to n (extremes included). It should work like this:
STk>(define (f x) (- 10 x)) f STk>(ever-negative? f 5) #f STk>(ever-negative? f 14) #tState whether your predicate generates an iterative or linear recursive process.
Write a procedure
(num-of-digits n) to count the number of digits
in the decimal representation of the positive integer n.
[Hint: use (quotient a b), which returns the quotient of
a divided
by b to divide suucessively the number by 10..
For example, (quotient 3256 10) = 325, (quotient 325 10) = 32,
(quotient 32 10) = 3, (quotient 3 10) = 0.]
It should work like this:
STk> (num-of-digits 3256) 4 STk> (num-of-digits 3) 1Copyright: © 2000-2007 by the Regents of the University of Minnesota
Department of Computer Science and Engineering. All rights reserved.
Comments to: Maria Gini
Changes and corrections are in red.