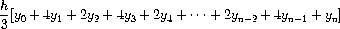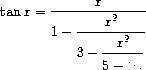CSci 1901: Lab 4, February 8

Lab 4: More RSA Encryption

• Lab 4 Template

For this lab we will extend the RSA encryption method we began in Lab3 to encode and decode messages. Recall that RSA requires that you select 2 large prime numbers, p and q, from which you compute n=p*q and m=(p-1)*(q-1). Next you select a number e such that e is greater than 1 and less than n, and that e and m are relatively prime, i.e. gcd(e,m)=1. Finally you compute d such that d*e mod m = 1.

Your public key is the pair (* p q) and e. e is called the public exponent, n=(p*q) is called the modulus. Your private key is the pair (* p q) and d. d is called the private exponent.

Step 1 (Drill)

Write the procedure, (sum-list lst), which takes in a list of numbers and returns the sum of all of the elements of the list.

STk> (sum-list (list 1 2 4))
7
STk> (sum-list (list 1))
1
STk> (sum-list (list 1 1 1 0 0 0 2 2 2 3))
12
STk> (sum-list (list))
0
STk> (sum-list (list 1 2 3 4 5))
15

Write the procedure (sum-primes lst) that takes in a list of numbers and returns the sum of all of the elements of the list that are prime. Like last week, the lab template contains the predicate (prime? n) that you may make use of.

STk> (sum-primes (list 3 4 5 6 7))
15
STk> (sum-primes (list 3 3 4 4 3))
9
STk> (sum-primes (list 3))
3
STk> (sum-primes (list 4))
0
STk> (sum-primes (list))
0

2 points

Step 2 (Drill)

STk> (filter-odds (list 1 2 3 4 5 6 7 8))
(2 4 6 8)
STk> (filter-odds (list 2 2 3 3 6))
(2 2 6)
STk> (filter-odds (list 2 4 6 8 10))
(2 4 6 8 10)
STk> (filter-odds (list 3 5 101 71))
()

2 point

Step 3 (Application - RSA Encryption)

(define (make-public-key e n) (cons e n))
(define (public-exponent public-key) (car public-key))
(define (public-modulus public-key) (cdr public-key))

Write a similar constructor make-private-key for private keys. Also write the appropriate accessor methods - private-exponent and private-modulus.

Now copy your definitions for my-p, my-q, my-n, my-m, my-e, and my-d from last weeks lab into this weeks lab, and add the following definitions for my-public-key and my-private-key.

(define my-public-key (make-public-key my-e my-n))
(define my-private-key (make-private-key my-d my-n))

1 point

Steps 4(Application - RSA Encryption)

Rewrite encrypt from last week's lab so that instead of taking in values for e and n directly it just takes in a public-key. To obtain the value corresponding to what was e, extract it from the public-key data structure using (public-exponent public-key). Likewise use public-modulus to obtain what was n.

The procedure was of the form (encrypt word e n), and the new one should have the form (encrypt word public-key).

Repeat this process to rewrite the decrypt procedure to use your private-key abstraction instead of d and n directly.

encrypt and decrypt should now work as follows:

 
STk> (encrypt 'hello my-public-key)
21535366738991243783161928400 
STk> (decrypt 21535366738991243783161928400  my-private-key) 
hello

2 points

Part 5 (Application - RSA Encryption)

• Write a procedure to encrypt one by one the words in a list and produce a list of encrypted words. This procedure should use the procedure to encrypt a single word you just wrote. This new procedure takes a whole list of words and a public key converts them to encoded numbers. The way to pass these words into the procedure is as a list, denoted by the apostrophe character before the open parentheses. Your procedure should scan down the list, encrypting each word as it goes and finally returning a whole list of encoded numbers. These numbers should be in the correct order left to right. Using the same keys as before, it should work like this:

  STk> (list-encrypt '(hello there) my-public-key) 
  (21535366738991243783161928400 20995383430717601169654110978)  
  STk> (list-encrypt '(C programmers do not die they get cast into void) my-public-key)
  (14620941571469012153935306931 20646050938108459644373803779
  5448837548714002262470184355 22167283850878867480524467992
  18099790359573697190186591731 27155808237763629481455263584
  1822899848115866044786583558 19397463663947691797552440098
  8022303303235824719972853107 10318394737664924709403341322)  
  STk> (list-encrypt '(scheme programmers get garbage collected) my-public-key)
  (10667884398433131202378347401 20646050938108459644373803779
  1822899848115866044786583558 12475564237783808140885630531
  9890658091149305891075744194) 
  

• Get the public key of someone else in the class, encrypt a message using his/her public key, and send him or her the encrypted message. The person whose public key you used will be able to decrypt the message.

• Write a procedure to decrypt one by one the words in a list and produce a list of words. This time you want to be able to decrypt a list of encoded numbers that someone else has encrypted, so your procedure should use the decrypt procedure you defined above. It should scan down the list and decrypt the words one by one. You should end up calling the procedure like this:

  STk> (list-decrypt 
  '(14620941571469012153935306931 20646050938108459644373803779
  5448837548714002262470184355 22167283850878867480524467992
  18099790359573697190186591731 27155808237763629481455263584
  1822899848115866044786583558 19397463663947691797552440098
  8022303303235824719972853107 10318394737664924709403341322) 
  my-private-key)
  (c programmers do not die they get cast into void)
  STk> (list-decrypt  
  '(10667884398433131202378347401 20646050938108459644373803779 
  1822899848115866044786583558 12475564237783808140885630531 
  9890658091149305891075744194) my-private-key)
  (scheme programmers get garbage collected)
  

• Decrypt a message sent to you by someone else in the class. Verify things are correct by sending back the decrypted message in plain text.

3 points

Bonus Question

1. Exercise 1.29, which is on using the Simpson rule to compute the integral of a n function f between a and b. The Simpons rule is as follows
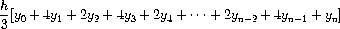
   where h = (b - a)/n, for some even integer n, and yk = f(a + kh). (Increasing n increases the accuracy of the approximation.)
   Define a procedure that takes as arguments f, a, b, and n and returns the value of the integral, computed using Simpson's Rule. Use your procedure to integrate cube between 0 and 1 (with n = 100 and n = 1000).
2. Exercise 1.39 which is approximating the tangent function using the continued fraction representation
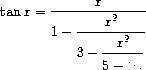
   where x is in radians. Define a procedure (tan-cf x k) that computes an approximation to the tangent function based on Lambert's formula. K specifies the number of terms to compute.
   How large must you make k in order to get an approximation that is accurate to 4 decimal places?

Congratulations on completing Lab 4!
Lab 4 point total: 10 pts