- in Python 0 is considered False. Look at what this can cause:
>>> def even(x): ... """ convoluted way of defining even. In Python 0 is False, so ... when x%2 is 0, i.e. the number is even, the condition is false. ... if x%2: # when x is even x%2 is 0, i.e. False ... return False ... else: ... return True ... >>> def even(x): ... """better definition: when x%2 is False the number is even""" ... return not x%2 ... >>> def even(x): ... """better definition: checks explicitely if x%2 is 0""" ... return x%2==0 ...
- Many list operations mutate the list, so if we want to keep the
original list, we need to make a copy (which is called a clone in
Python). For instance:
>>> d=[[1,7],[3,8],[10,5]] >>> g=d[:] # make a copy >>> g.reverse() # reverse the copy >>> g [[10, 5], [3, 8], [1, 7]] >>> d # d is unchanged [[1, 7], [3, 8], [10, 5]]
- assignments and mutation can be confusing. Let's see some more
examples.
>>> a=[1,2] >>> b=a >>> c=b
a, b, c are bound to the same list. A change made to one variable affects all the others:>>> a[1]=100 # this is like (set-car! (cdr a) 100) >>> a [1, 100] >>> b [1, 100] >>> c [1, 100]
The assignment of a new binding to a variable does not change the list object the variable was bound to, it just rebinds the variable>>> b=[7,8] >>> b # b is changed -- this is like (set! b (list 7 8)) [7, 8] >>> c # but c and a are not [1, 100] >>> a [1, 100]
However, an augmented assignment, such as += or L.append, changes the list object, so causing changes in all the variables that are bound to it:>>> a += [30] # change a by attaching 30 to the end of a >>> a [1, 100, 30] >>> c # c changes too! [1, 100, 30]
- Scoping rules: use of global variables
When a variable is used inside a function it is assumed to be a local variable, unless it is declared to be global.count=0 # this is a global counter def incf_count(x=1): # x=1 means that 1 is the default value of x """ increments the global variable count by x (1 default value)""" global count # we want to access the global variable count +=x return count - Scoping rules. Python uses lexical scope, but the variables
accessible in the parent environment can only be read, not written.
This is because Python passes variables by value when they are simple
variables. However, sequences or objects are passed by reference and
so they can be modified. Let's see this with an example.
def f(y): """ Python passes variables by value (unless they are sequences or objects) so non local variables can be read but not modified""" x = 0 def g(y): x = x+y # this generates an error return x return g(y) # we can see the error when we try it >>> f(1) Traceback (most recent call last): File "This is useful if we want to create an object that keeps its own state.", line 1, in ? File "test.py", line 8, in f return g(y) File "test.py", line 6, in g x = x+y; # this generates an error UnboundLocalError: local variable 'x' referenced before assignment # we get around the problem by using a list instead of a simple variable def f(y): """ a closed variable can be modified if it is a sequence or object. Sequences and objects are passed by reference""" x = [0] # x is a list def g(y): x[0] += y # so we can modify it return x[0] return g(y) >>> def make_accumulator(n): ... """makes an accumulator -- specify how much you want to increment """ ... acc=[n] # need to use a list to allow rewrite of the variable ... def incf(x): ... acc[0] += x ... return acc[0] ... return incf ... >>> acc1 = make_accumulator(2) 2 >>> acc1(10) 12
- when a variable is passed by reference, changing the local variable
in a function changes the data structure passed, so the
variable in the calling environment is modified.
>>> def attach(x,y): ... x.append(y) # this modifies the variable passed for x ... return x ... >>> a=[1,2,3] >>> attach(a,33) [1, 2, 3, 33] >>> a [1, 2, 3, 33]
Wednesday, April 26
- Pop11 quiz
QUESTION 1: You are given the following two functions to attach an element to the end of a list. def attach(x,y): """attaches element y to the end of list x""" x.append(y) return x def attach2(x,y): """attaches element y to the end of list x""" x += [y] return x Fill in the answers: >>> a = [1,2,3] >>> b = [4,5] >>> attach(a,33) ......................................................... >>> a ......................................................... >>> attach2(b,55) ......................................................... >>> b ......................................................... QUESTION 2: Fill in the blanks assuming these are evaluated in sequence >>> a=[1,2] >>> b=a >>> c=b >>> a[0]=100 >>> a ......................................................... >>> b ......................................................... >>> b=[7,8] >>> b ......................................................... >>> a ......................................................... >>> a += [30] # attaches [30] to end of a >>> c ......................................................... - Some practice on iterations.
Write a function subst(old,new,seq) to substitute an element with a
new element in a sequence, to do something like:
>>> subst('a',o','nice warm day') nice worm doyHere are sone of the solutions suggested by students:def subs(old,new,lst): """substitutes old with new in lst modifying the sequence""" counter = -1 # counter is used as index in lst for element in lst: counter += 1 if element == old: lst[counter]=new return lst def subs2(old,new,lst): """substitutes old with new in lst modifying the sequence""" for x in range(len(lst)): if lst[x]==old: lst[x]=new return lst def subs3(old,new,lst): """substitutes old with new in lst creating a new sequence""" result = [] for x in lst: if x==old: result.append(new) else: result.append(x) return resultNotice the difference between a function that creates a new sequence, and so works on immutable sequences, and a function that modifies the sequence, and so works only on mutable sequences. - Dictionaries are used in Python to index a mutable data structure on
something more complex than just a numerical index. A dictionary is a
collection of pairs of the form
key:value, where the elements of a pair are a (unique) key and the value associated to it. Keys are immutable, so a string, number, or tuple of immutable things can be used for key.
Pairs are collected into a dictionary by separating them by commas and surrounding the entire collection with {}. There is no ordering in a dictionary. A key/value pair is added to a dictionary by assigning the value to the element indexed by the key. If the key does not exist, it is created and added to the dictionary, if not the value is changed. The value of a key is retrieved by specifying the key as an index. A list of pairs can be converted to a dictionary using the functiondict - Let's start with basic examples of dictionaries:
>>> phone_list={} # create dictionary >>> phone_list['john']=457 # add key/value >>> phone_list {'john': 457} >>> phone_list['bill']=767 # add another key/value >>> phone_list {'john': 457, 'bill': 767} >>> phone_list['john']=657 # change value >>> phone_list {'john': 657, 'bill': 767} >>> new_phones=dict([['joe',457],['mary',587],['joe',357]]) >>> new_phones # the last value is used in dictionary {'joe': 357, 'mary': 587} - Let's look at some of the methods for dictionaries used most often:
>>> phone_list.items() # returns a copy of the list of items [('john', 657), ('bill', 767)] >>> phone_list.keys() # a copy of the list of keys ['john', 'bill'] >>> phone_list.values() # a copy of the list of values [657, 767] >>> phone_list.get('joe') # get value for given key >>> phone_list.get('john') 657 >>> phone_list.has_key('joe') # check if key exists False >>> for key in phone_list.keys(): ... print key, phone_list[key] ... john 657 bill 767A powerful method for dictionaries is update.D.update(D1)for eack keykinD1, setsD[k]equal toD1[k]. This allows merging dictionaries:>>> phone_list.update(new_phones) # update phone_list with values in new_phones >>> phone_list {'mary': 587, 'john': 657, 'bill': 767, 'joe': 357} >>> phone_list.items() # returns a copy of the list of items [('mary', 587), ('john', 657), ('bill', 767), ('joe', 357)]The Methods defined on dictionaries are:>>> dir(phone_list) ['__class__', '__cmp__', '__contains__', '__delattr__', '__delitem__', '__doc__', '__eq__', '__ge__', '__getattribute__', '__getitem__', '__gt__', '__hash__', '__init__', '__iter__', '__le__', '__len__', '__lt__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__setitem__', '__str__', 'clear', 'copy', 'fromkeys', 'get', 'has_key', 'items', 'iteritems', 'iterkeys', 'itervalues', 'keys', 'pop', 'popitem', 'setdefault', 'update', 'values']
- A dictionary can be constructed using list comprehension to construct a
list of tuples, from which we can then obtain a dictionary using
dict. The advantage of this is that duplicate keys are removed:>>> a="this is too long" >>> [(x,a.count(x)) for x in a] [('t', 2), ('h', 1), ('i', 2), ('s', 2), (' ', 3), ('i', 2), ('s', 2), (' ', 3), ('t', 2), ('o', 3), ('o', 3), (' ', 3), ('l', 1), ('o', 3), ('n', 1), ('g', 1)] >>> d = dict([(x,a.count(x)) for x in a]) >>> d # characters and occurrences {' ': 3, 'g': 1, 'i': 2, 'h': 1, 'l': 1, 'o': 3, 'n': 1, 's': 2, 't': 2} - Tables in Scheme are equivalent to dictionaries in Python. Since dictionaries are implemented as hash tables, they are more efficient than the Scheme implementation of tables using list. Of course, we could implement tables in Scheme using hash tables as well (not all Scheme implementations support hash table, since hash tables are not in the standard).
Friday, April 28
- Comments on mistakes made in POP11. Look at older class notes on scoping of variables and on assignment and mutation.
- There is a difference between objects (such as lists, sequences, etc)
which appear on the right end side of the assignment
and references to objects (variables), which appear on the left end side
of the assignment. This is an important distinction,
essential to fully understand assignments.
- a regular asssignment either creates a target object or rebinds
the target reference.
>>> a = 3 # reference a is created and bound to 3 3 >>> a = 4 * a # reference a is rebound to new object 12
- an augmented assignment, such a += or *=, modifies the object to
which the reference is bound. The reference must already be bound.
>>> b += 3 # error, reference is not bound >>> a += 7 # the object to which referenec a is bound is modified 19
- a regular asssignment either creates a target object or rebinds
the target reference.
- Some more on scope of variable. Python is much like Scheme when it
comes to scope of variables.
Python passes variables by value when they are simple variables, and by
reference when they are sequences or objects. Passing by reference
allows modifying the object passed.
>>> a=3 # this is the first a >>> def f(a): ... a=5 # this is the second a -- it is a different a ... return a ... >>> a # the first a 3 >>> f(a) 5 >>> a # unchanged 3
The same happens in Scheme:STk> (define a 3) ; this is the first a STk> (define (f a) (set! a 5) ; this is the second a -- it is a different a a) f STk> a ; the first a 3We can see what happens when a list is passed:>>> b=[3] # this is the first b >>> def ff(b): ... b[0]=5 # the second b- bound to the same object as the first ... return b ... >>> ff(b) [5] >>> b # b is changed [5]
The same happens in Scheme:STk> (define b (list 3)) ; this is the first b b STk> (define (ff b) (set-car! b 5) ; the second b- bound to the same object as the first b) ff STk> (ff b) (5) STk> b (5)
Monday, April 30
Today we will talk about classes. Let's work through a simple example, similar to the bank account in Scheme. Instead of creating a bank account by returning a lambda expression as in Scheme, we create a bank account by creating an instance of a class. We need to define the class BankAcct first, and to create instances of it. Let's look at the class definition first. You'll notice the use of self. It is a way of specifying the operation will be done on the instance, but the class does not have a name for the instance, so self is a general way of referring to the object itself.class BankAcct: """make a bank account using python's native class structure.""" # a class variable: one per class, not one per instance. # we will use it to keep track in the class of all the instances ListOfAccts=[] # initialization method. Executed every time an instance is created def __init__(self): print 'creating a bank acct.' self.amount = 0 # initialize to 0 amount self.ListOfAccts.append(self) # add to list of accounts def deposit(self,amt): self.amount = self.amount + amt # update amount as needed return self.amount def balance(self): return self.amountNow let's use the class:>>> bill=BankAcct() # create an instance creating a bank acct. >>> john=BankAcct() creating a bank acct. >>> anne=BankAcct() creating a bank acct. >>> bill.balance() # use a method from the class 0 >>> bill.amount # access directly the class variable, not as clean 0 >>> bill.deposit(50) 50 >>> bill.balance() 50 >>> bill.amount 50 >>> BankAcct.ListOfAccts # this is a class variable not an instance variable [<__main__.BankAcct instance at 0x1bd260>, <__main__.BankAcct instance at 0x1bd558>, <__main__.BankAcct instance at 0x1bd648>] >>> def totalaccounts(): # compute total money in bank ... total=0 ... for x in BankAcct.ListOfAccts: ... total += x.amount ... return total ... >>> totalaccounts() 50
Week 1 - Intro to Scheme
This week we will start with the basic aspects of SchemeWednesday. January 17
Introduction to the objectives of the course and to Scheme. Why we learn Scheme.Friday, January 19
- the rules of evaluation in Scheme. Primitive elements. Compound expressions. Special forms. Why we need special forms.
- the use of
defineto create variables and to create procedures. - Exercise: write a procedure to find the largest element among three
numbers. For this exercise you are not allowed to use the system defined
procedure
max.
Here are some of the solutions proposed (the ones I wrote down):;;; find the maximum of 3 numbers ;; this is correct but hard to read and verify because of the nested ifs (define (max_of3 x y z) (if (> x y) (if (> x z) x (if (> y z) y z)) (if (> y z) y z))) ;; this solution uses the fact tha > takes more than 2 arguments. ;; It does not work when some of the elements are the same. It can ;; be fixed by replacing > with >= (define (max_of3 x y z) (if (> x y z) x (if (> y x z) y (if (> z y x) z)))) ;; nice and easy to read, but does not handle the case of equal numbers ;; It can be fixed by replacing > with >= (define (max_of3 x y z) (cond ((and (> x y) (> x z)) x) ((and (> y x) (> y z)) y) ((and (> z x) (> z y)) z)))
Week 2 -- recursion
This week we will learn how to write more complex procedures and we will learn about recursion as a way of decomposing problems.Monday, January 22
- Finish the problem of finding the maximum of 3 numbers. The idea
suggested last week is to solve the problem by solving a simpler problem,
i.e. find the maximum of 2 numbers.
;; this decomposes the problem into a simpler one - finding the max ;; of 2 numbers. It is easier to check and to extend. ;; define the max of 2 numbers -- recall max is already defined ;; but we define here to understand how to do it. (define (max x y) (if (> x y) x y)) ;; and then the max of 3 numbers (define (max_of3 x y z) (max x (max y z))) ;; this is similar to the previous one. Any reason to chose one over the ;; other? (define (max_of3 x y z) (max (max x y) z)) - New problem: define the median of 3 numbers. The median is
the middle number when the three numbers are sorted.
[For more than 3 numbers, the median is the number that splits the
collection in two, leaving at most half of the elements below the
median and half above. For an even number of
elements the median if often the mean of the two middle values.]
Here are some of the solutions proposed.;; find the median of 3 numbers ;; this is easy to read, but it requires having max_of3 (define (median_of3 x y z) (cond ((= x (max_of3 x y z)) (max y z)) ((= y (max_of3 x y z)) (max x z)) ((= z (max_of3 x y z)) (max x y)))) ;; same as above. Short, easy to read but a bit convoluted, requires max_of3. (define (median_of3 x y z) (- (+ x y z) (max_of3 x y z) (min_of3 x y z))) ;; this uses the same idea as for max_of3 and computes min and max of ;; 2 numbers to build the solution (define (median_of3 x y z) (min (max x y) (min (max y z) (max z x))))
Wednesday, January 24
-
Recursion is a powerful way of solving problems by decomposing them
into "simpler" problems of the same type and one or more basic cases.
Any recursive procedure should contain at least one of each of the
following:
- an exit condition
- a recursive call
- Example: write a recursive procedure to add all the integers in the
range
lowtohigh, wherelowis less or equal tohigh. In the caselow=highadd the number to itself.
To understand how to solve this recursively, we can work through a simple example. Suppose we have to add the numbers from 1 to 4. The result will be 1+2+3+4. We can write this as (1 + (2 + (3 + 4))). This suggest a recursive step where we add 3 to the result of adding the numbers from 4 to 6. We need to continue until we run out of numbers. This produces the following procedure:(define (sumrange low high) (cond ((= low high) high) (else (+ low (sumrange (1+ low) high)))))
where1+is a predefined procedure that adds 1 to its argument.
We can instead think of our example as (((1 + 2) + 3) + 4), which will produce:(define (sumrange low high) (cond ((= low high) high) (else (+ (sumrange low (1- high)) high))))
where1-is a predefined procedure that subtracts 1 from its argument.
Suppose we want to change the procedure as follows: when the two arguments are the same, return their sum.(define (sumrange low high) (cond ((= low (- high 1) (+ low high)) ;; this is used only when the two arguments are equal ((= low high) (+ low high)) (else (+ low (sumrange (1+ low) high))))))
Friday, January 26
-
When we write programs we need to understand how the way programs are
written affects the time and space needed to compute them.
A problem can be solved in different ways, which may produce different
orders of growth of the computation. We can start understanding what this
means by looking at the structure (i.e. how the recursive calls are made)
in prodedures.
-
This is the problem we did last time:
(define (sumrange low high) (cond ((= low high) high) (else (+ low (sumrange (1+ low) high)))))
If the range is huge, there are many recursive calls and a lot of stack space is needed. Can we write this program differently? - Other problems to think about:
- add the numbers in a given range that satisfy a property, such as being prime. This is similar to the previous problem, but we need to add only the numbers that are prime.
- count the numbers in a given range that satisfy a property, such as being prime. This is also similar, but we need to count the numbers instead of adding them.
- find the smallest number in a given range that satisfy a property, such as being prime. This is different because as soon as we find the element we are looking for, we stop the recursion. To avoid getting into an infinite loop we have to check that an element with the required property exists in the range.
- First pop quiz: (1) compute some values of the Ackerman function and (2) Write a procedure that takes in three numeric arguments and returns the largest argument minus the smallest.
Week 3 - complexity
This week we will learn about complexity of procedures. We will learn how to control complexity by understanding the computational process that different procedures generate and we will learn how to speed up computations by thinking about clever algorithms.Friday, February 1 and Monday, February 5
Here are the files John used in during his lectures.
- Presentation (pdf)
- let.scm
- lambda.scm
- sums.scm - Only went over a little of this file, the rest is intresting though...
Monday, January 29
- The procedure we wrote last week for sumrange generates
a linear recursive process. We can see why it is a linear recursive
process from the single recursive call (+ low (sumrange (1+ low)
high). This is because sumrange is called from inside
another procedure, +. This produces a chain of deferred
operations, which grows linearly with the number of integers to sum up,
hence the name linear recursive process.
We can see what happens by tracing the procedure:STk> (trace sumrange) STk> (sumrange 2 6) .. -> sumrange with low = 2, high = 6 .... -> sumrange with low = 3, high = 6 ...... -> sumrange with low = 4, high = 6 ........ -> sumrange with low = 5, high = 6 .......... -> sumrange with low = 6, high = 6 .......... <- sumrange returns 6 ........ <- sumrange returns 11 ...... <- sumrange returns 15 .... <- sumrange returns 18 .. <- sumrange returns 20 20
- We can write sumrange differently to generate a
linear iterative process. The idea is to replace the call to +
outside the recursive call with some computation inside the
recursive call. We can achieve this by adding a new parameter to the
procedure and using the parameter to accumulate the partial results of the
summation.
(define (sumrange low high) (define (sum-iter a low) (if (= low high) (+ a high) (sum-iter (+ a low) (1+ low)))) (sum-iter 0 low))This procedure uses a nested procedure, sum-iter to do the iteration. The parameter a is used to accumulate the partial sum. The internal procedure sum-iter uses the value of high from the enclosing environment.
To see more clearly the two procedures, we can write them as separate procedures. We will have to add high as an argument to sum-iter because it is not longer visible.(define (sumrange low high) (sum-iter 0 low high)) (define (sum-iter a low high) (if (= low high) (+ a high) (sum-iter (+ a low) (1+ low) high)))We can see what happens while computing by tracing the procedures:STk> (trace sumrange) sumrange STk> (trace sum-iter) sum-iter Tk> (sumrange 2 6) .. -> sum-iter with a = 0, low = 2, high = 6 .... -> sum-iter with a = 2, low = 3, high = 6 ...... -> sum-iter with a = 5, low = 4, high = 6 ........ -> sum-iter with a = 9, low = 5, high = 6 .......... -> sum-iter with a = 14, low = 6, high = 6 .......... <- sum-iter returns 20 ........ <- sum-iter returns 20 ...... <- sum-iter returns 20 .... <- sum-iter returns 20 .. <- sum-iter returns 20 20
- To practice, try answering Exercise 1.9 (page 36), Exercise 1.11 (page 42), and Exercise 1.12 (page 42).
Wednesday, January 31
We will look at how to make faster programs by being more careful in how we write programs. We will look, in particular at the problem of finding if a number is prime. Read the material in the textbook on exponentiation (Section 1.2.4) and on prime numbers (Section 1.2.6)Try solving Exercise 1.16 (page 46), Exercise 1.17 (page 46), Exercise 1.25 (page 55), and Exercise 1.26 (page 55).
Friday, February 2
Week 4 - lists
This week we will learn about writing constructors and selectors to build and access abstract data types. We will work in particular on sequences or lists.Wednesday, February 7
- the constructors and selectors for lists are cons, car, cdr. We also need null? to chech if a list is empty. This is because we do not know how many elements are in a list.
- example: Add all the elements of a list
(define (sum_l l) (if (null? l) () (+ (car l)(sum_l (cdr l)))))
Friday, February 9
How lists are represented and more examples of using lists. Here are the problems we did in class:- Write a predicate to find if a given element is in a list. A predicate is a procedure which returns #t or #f.
- Write a procedure that takes in a list and returns a list of all the even numbers from the input list. We typically solve this type of problem by writing a procedure that generates a linear recursive process.
Week 5 - lambda, let, filter
Monday, February 12
- more examples of lambda and let.
- lambda is used implicitely when we use define to
define a procedure.
(define (foo x y) (* x y)) is the same as (define foo (lambda (x y) (* x y)))
lambda creates a procedure without assigning it a name. - let is "syntactic sugar" for lambda. We use
let to create local variables.
(let ((x 1) (y 2)) (+ x y))
is equivalent to((lambda (x y) (+ x y)) 1 2)
- lambda is used implicitely when we use define to
define a procedure.
- First quiz. The quiz will returned on Thursday.
Wednesday, February 14
Today we will work on more examples of recursion on lists. We will learn about patterns, or templates, we can use to abstract similar operations. In the case of lists, we have already seen some of the patterns:- map -- this is used when a function is to be applied to each element
of a list, and a list of the results of the application returned. Examples
are: double all the elements of a list. increment by one all the elements of
a list, etc. We can write this pattern using recursion
(define (my-map fn l) (if (null? l) () (cons (fn (car l))(my-map fn (cdr l))))) (define (double-l l) (my-map (lambda (x) (* 2 x)) l)) (define (inc-l l) (my-map 1+ l))and doSTk> (double-l (list 3 4 9)) (6 8 18) STk> (inc-l (list 5 3 8)) (6 4 9) STk> (my-map 1+ (list 5 3 8)) (6 4 9)
map is used so many times, that it is already defined. map is more general. It accepts a function of more than 1 argument and as many lists as the number of arguments of the function. The lists have to have the same length. For instance
STk> (map + (list 1 2 3) (list 10 20 30)) (11 22 33)
- filter -- this is used when we need to select elements from a list that
satisfy a given property and return a list of all of them. For instance, find
all the even numbers, or all the prime numbers, or all the multiples of 3,
etc. Filter is used often, but is not predefined in Scheme.
(define (filter pred l) (cond ((null? l) ()) ((pred (car l)) (cons (car l) (filter pred (cdr l)))) (else (filter pred (cdr l)))))
So, we can write things such asSTk> (filter even? (list 3 4 89 6 5)) (4 6) STk> (filter (lambda (x) (= (remainder x 3) 0)) (list 25 3 5 9 33))) (3 9 33)
- accumulate -- this is used when we want to accumulate, using a
specific accumulator function such as + or *, the elements of the list
and return the accumulated valued. This will work to add all the elements
of a list, or multiply them.
;; combiner is a procedure of two args that combines the elements of the list ;; null-value specifies what value to use when the elements of the list run out. (define (accumulate combiner l null-value) (if (null? l) null-value (combiner (car l) (accumulate combiner (cdr l) null-value))))We can write things such asSTk> (accumulate + (list 1 2 3) 0) 6 STk> (accumulate * (list 2 6) 1) 12
- Question: can we use accumulate to count the elements of a list? Do we need to modify it into a more abstract pattern?
Friday, February 16
- pop quiz #3.
You are asked to write a procedure double-odd that takes in a list and returns a list containing the double of every element in the input list which is odd. It should work like this:STk> (double-odd (list -3 8 -1 4 5)) (-6 -2 10) STk> (double-odd (list -2 2 4)) () STk> (double-odd (list -1 3)) (-2 6)
Do the following steps:- Which of the following abstractions can be used for the
procedure you have to write? Check all that apply.
map filter accumulate - Assuming you have procedures for the abstractions listed above, i.e. (filter pred lst), (map proc lst), (accumulate proc lst end), write the procedure double-odd using the abstractions.
- Which of the following abstractions can be used for the
procedure you have to write? Check all that apply.
- how to write procedures that operate on lists and generate a linear
iterative process.
- We have written filter as a procedure that generates a linear
recursive process:
(define (filter pred lst) (cond ((null? lst) ()) ((pred (car lst)) (cons (car lst) (filter pred (cdr lst)))) (else (filter pred (cdr lst)))))
To generate a linear iterative process, we need to replace (cons (car lst) (filter pred (cdr lst))) with a call to filter and pass the partial result of the computation as an additional argument.(define (filter pred lst) (filter-i pred lst ())) (define (filter-i pred lst result) (cond ((null? lst) result) ((pred (car lst)) (filter-i pred (cdr lst) (cons (car lst) result))) (else (filter-i pred (cdr lst) result))))
We can see how this works by tracing:STk> (trace filter-i) filter-i STk> (filter odd? '(2 1 5)) .. -> filter-i with pred = #[subr odd?], lst = (2 1 5), result = () .... -> filter-i with pred = #[subr odd?], lst = (1 5), result = () ...... -> filter-i with pred = #[subr odd?], lst = (5), result = (1) ........ -> filter-i with pred = #[subr odd?], lst = (), result = (5 1) ........ <- filter-i returns (5 1) ...... <- filter-i returns (5 1) .... <- filter-i returns (5 1) .. <- filter-i returns (5 1) (9 5 1)
The result is in reverse order! this is because every time we find an element which satisfies the filter, we "push" it in front of the resulting list. Think of cons as an operation that pushes something on the top of a stack. The first element that satisfies the filter is the first to be pushed, so it ends up being the one at the bottom of the stack.
Let's try to build the list by adding elements at the end:(define (filter-i pred lst result) (cond ((null? lst) result) ((pred (car lst)) (filter-i pred (cdr lst) (cons result (car lst)))) (else (filter-i pred (cdr lst) result))))
We end up with something that is not a list:STk> (trace filter-i) filter-i STk> (filter odd? '(2 1 5)) .. -> filter-i with pred = #[subr odd?], lst = (2 1 5), result = () .... -> filter-i with pred = #[subr odd?], lst = (1 5), result = () ...... -> filter-i with pred = #[subr odd?], lst = (5), result = (() . 1) ........ -> filter-i with pred = #[subr odd?], lst = (), result = ((() . 1) . 5) ........ <- filter-i returns ((() . 1) . 5) ...... <- filter-i returns ((() . 1) . 5) .... <- filter-i returns ((() . 1) . 5) .. <- filter-i returns ((() . 1) . 5) ((() . 1) . 5)
So, let's go back to our earlier definition and reverse the result. There is a predefined procedure,<reverse, to reverse a list. We can call reverse here(define (filter pred lst) (reverse (filter-i pred lst ())))
or here(define (filter-i pred lst result) (cond ((null? lst) (reverse result)) ((pred (car lst)) (filter-i pred (cdr lst) (cons result (car lst)))) (else (filter-i pred (cdr lst) result))))
- Scheme has a predefined procedure to reverse a list, but we can try to write it. From the example we saw for filter, it should be very easy to write reverse to generate a linear iterative process, whil it is will be more difficult to write it to generate a linear recursive process. Try to write it.
- Can you think how to use filter to reverse a list?
- We have written filter as a procedure that generates a linear
recursive process:
Week 6 - trees
Monday, February 19
Midterm examWednesday, February 21
We will start working on more complex data structures, in particular on hierarchical data structures (often called nested lists or trees).- how is a nested list represented internally
- patterns for operations on trees. When we have to traverse a tree,
element by element and do some operation, such as counting the elements
of the tree, etc here is the pattern to use:
(define (count-leaves tree) (cond ((null? tree) 0) ; null value ((not (pair? tree)) 1) ; got one element (else (+ (count-leaves (car tree)) ; count the elements in the car (count-leaves (cdr tree)))))) ; and the ones in the cdrIf instead we want to add the elements in a tree, the pattern is the same, with small changes:(define (sum-tree tree) (cond ((null? tree) 0) ; null value ((not (pair? tree)) tree) ; add one element (else (+ (sum-tree (car tree)) ; add the elements in the car (sum-tree (cdr tree)))))) ; and the ones in the cdrTo make a copy of tree:(define (copy-tree tree) (cond ((null? tree) ()) ; null value ((not (pair? tree)) tree) ; reached a leaf (else (cons (copy-tree (car tree)) ; copy the car (copy-tree (cdr tree)))))) ; and the cdrIf we want to find the largest element in a tree (assuming at least one element is positive):(define (max-tree tree) (cond ((null? tree) 0) ; null value ((not (pair? tree)) tree) ; reached a leaf (else (max (max-tree (car tree)) ; the max of the elements in car (max-tree (cdr tree)))))) ; and of the ones in cdr
Friday, February 23
- Pop quiz 4:
[This is a question in lab 6] You are given the following partially
defined procedure:
(define (subsets s) (if (null? s) (list ()) (let ((rest (subsets (cdr s)))) (append rest (map ??? rest))))) and the following traces of the complete procedure: STk> (subsets (list 2)) .. -> subsets with s = (2) .... -> subsets with s = () .... <- subsets returns (()) .. <- subsets returns (() (2)) (() (2)) STk> (subsets (list 1 2)) .. -> subsets with s = (1 2) .... -> subsets with s = (2) ...... -> subsets with s = () ...... <- subsets returns (()) .... <- subsets returns (() (2)) .. <- subsets returns (() (2) (1) (1 2)) (() (2) (1) (1 2))Study the traces and look at the difference betweenSTk> (subsets (list 2)) (() (2)) STk> (subsets (list 1 2)) (() (2) (1) (1 2))
1. Mark in the list above the part that corresponds to (subsets (list 2)). 2. Write the rest of the list above after removing the elements that correspond to (subsets (list 2)). 3. Compare the result of question 2 with the result of question 1. Explain how do the two lists differ. 4. Now you should we able to complete the missing code:(define (subsets s) (if (null? s) (list ()) (let ((rest (subsets (cdr s)))) (append rest (map _______________________________ rest))))) - Double the elements of a tree. How to write it using map:
(define (double-tree tree) (if (pair? tree) (map (lambda (x) (double-tree x)) tree) (* 2 tree))) - We can now generalize it and write a procedure that maps a given
procedure to the elements of a tree. We simply add an additional argument,
the procedure to be applied:
(define (tree-map proc tree) (map (lambda (x) (if (pair? x) (tree-map proc x) (proc x))) tree))And now we can simply define(define (double-tree tree) (tree-map (lambda (x) (* 2 x)) tree)) (define (square-tree tree) (tree-map square tree)) ; assume square is defined
Week 7 - map, accumulate, sets
Monday, February 26
More practice on map and accumulate.- difference between list and append
- (accumulate cons () (list 1 2 3)) is the same as (cons 1 (cons 2 (cons 3 ())) wich is (1 2 3)
- we can define append using accumulate (as in lab 6)
(define (my-append seq1 seq2) (accumulate cons seq2 seq1))
Wednesday, February 28
- use of quote
- use of symbols
STk> (define bill 'tod) bill STk> bill tod STk> (define john bill) john STk> john bill
- sets: what is a set, how to represent a set. The material is in the textbook in the reading list for this week.
- Pop quiz 5
[This is exercise 2.36 from the textbook]
Exercise 2.36. The procedure accumulate-n is similar to accumulate except
that it takes as its third argument a sequence of sequences, which are all
assumed to have the same number of elements. It applies the designated
accumulation procedure to combine all the first elements of the sequences,
all the second elements of the sequences, and so on, and returns a
sequence of the results. For instance, if s is a sequence containing four
sequences, ((1 2 3) (4 5 6) (7 8 9) (10 11 12)), then the value of
(accumulate-n + 0 s) should be the sequence (22 26 30). Fill in the
missing expressions in the following definition of accumulate-n:
(define (accumulate-n op init seqs) (if (null? (car seqs)) () (cons (accumulate op init ??) (accumulate-n op init ??))))It should work like this:STk> (accumulate-n + 0 '((1 2 3) (4 5 6))) (5 7 9)
Friday, March 1
Review of the use of the binary tree representation for sets.- review of constructors and selectors
- to create a tree with one element we use (make-tree entry
left right). For instance:
STk< (define m (make-tree 6 () ())) m STk> m (6 () ())
- to add elements to a tree we should use the procedure
adjoin-tree. This guarantees the tree will be built correctly
according to the rules.
STk> (adjoin-tree 5 (adjoin-tree 42 m)) (6 (5 () ()) (42 () ())) STk> (adjoin-tree 0 (adjoin-tree 5 (adjoin-tree 42 m))) (6 (5 (0 () ()) ()) (42 () ())) STk> (adjoin-tree 5 (adjoin-tree 42 (adjoin-tree 0 m))) (6 (0 () (5 () ())) (42 () ()))
Even if the set has the same elements in all cases the tree might differ depending on the order in which the elements are inserted into it. If the elements are inserted in order, the tree is completely unbalanced. An unbalanced tree is of limited use, since the search time is proportional to the depth of the tree and an unbalanced tree is deeper than an equivalent balanced one.;; all children on left branch STk> (adjoin-tree 0 (adjoin-tree 5 (adjoin-tree 6 (make-tree 42 ()())))) (42 (6 (5 (0 () ()) ()) ()) ()) ;; all children on right branch STk> (adjoin-tree 42 (adjoin-tree 6 (adjoin-tree 5 (make-tree 0 ()())))) (0 () (5 () (6 () (42 () ()))))
- how to generalize this method of constructing a tree by adding elements one by one to a procedure that generates a tree from a list? [this is step 3 in lab 7]
Week 8 - sets
Monday, March 5
This week we will talk about using abstractions via constructor/selectors to hide details on data structure choices.- more on using binary trees to represent sets. Why use trees rather that an ordered list? efficiency is the major reason. If the tree is balanced the complexity drops from O(n) to O(log n), since at each step the size of the data is half the previous value. If the tree is not balanced the efficiency is not as dramatic.
- can multiple representations for sets coexist in the same program? How?
Wednesday, March 7
Here are the files John used in lecture:Friday, March 9
- No pop quiz for this week. Expect one after the break.
- Understanding how message passing works. We will start from the
example given in class on Wednesday:
(define (make-unordered-set lst) (define (empty) (null? lst) ) (define (count) (length lst)) (define (element-of-set? x set) (cond ((null? set) #f) ((eqv? (car set) x) #t) (else (element-of-set? x (cdr set))))) (define (dispatch op) (cond ((eq? op 'empty?) (empty)) ((eq? op 'count) (count)) ((equal? op 'element-of-set?) (lambda (el) (element-of-set? el lst))) (else "unknown op"))) dispatch) (define s1 (make-unordered-set (list 1 2 3)))- what is s1? it is a procedure, i.e. the procedure dispatch. the procedure takes one argument, the message.
- what do we get back when we send a message? it depends on how
dispatch is written. These are simple cases, the value is the
value of the call to an internal procedure:
STk> (s1 'empty?) #f STk> (s1 'count) 3
- what is this?
STk> (s1 'element-of-set?) #[closure ...]
When we get back a procedure #[closure..] in general it means we have to compute the value of the procedure, perhaps passing additional argument(s), as here:STk> ((s1 'element-of-set?) 6) #f STk> ((s1 'element-of-set?) 2) #t
- Let's make some changes. We add a parameter to some of the
internal procedures:
(define (make-unordered-set2 lst) (define (empty lst) (null? lst) ) (define (count lst) (length lst)) (define (element-of-set? x set) (cond ((null? set) #f) ((eqv? (car set) x) #t) (else (element-of-set? x (cdr set))))) (define (dispatch op) (cond ((eq? op 'empty?) (empty lst)) ((eq? op 'count) (count lst)) ((equal? op 'element-of-set?) (lambda (el) (element-of-set? el lst))) (else "unknown op"))) dispatch)- is this correct? yes.
- is passing the argument redundant? yes, but it can be useful for debugging, because we can now move the internal procedures outside the make-unordered-set2 constructor and we can see what they do.
(define (make-unordered-set3 lst) (define (empty) (null? lst) ) (define (count) (length lst)) (define (helper-element-of-set? x lst) (cond ((null? lst) #f) ((eqv? (car lst) x) #t) (else (helper-element-of-set? x (cdr lst))))) (define (element-of-set? x) (helper-element-of-set? x lst)) (define (dispatch op) (cond ((eq? op 'empty?) empty ) ((eq? op 'count) count ) ((eq? op 'element-of-set?) element-of-set? ) (else "unknown op"))) dispatch)- let's try a simple case:
STk> (define s1 (make-unordered-set3 (list 1 2 3))) s1 STk> (s1 'count) #[closure arglist=() 743c8]
What's happening? when the message count is received dispatch returns the procedure count, not its value. We can get its value by doing this:STk> ((s1 'count)) 3
and similarlySTk> ((s1 'element-of-set?) 2) #t STk> ((s1 'element-of-set?) 5) #f
- why did we write element-of-set? with 1 argument rather than 2?
- why did we write a helper procedure for element-of-set? instead of making the recursive call?
(define (make-unordered-set4 lst) (define (empty) (null? lst) ) (define (count) (length lst)) (define (element-of-set? x) (member x lst)) (define (dispatch op) (cond ((eq? op 'empty?) empty ) ((eq? op 'count) count ) ((eq? op 'element-of-set?) element-of-set? ) (else "unknown op"))) dispatch)- Let's try again. Now the value for 'element-of-set?is different
STk> (define s1 (make-unordered-set4 (list 1 2 3))) s1 STk> ((s1 'element-of-set?) 2) (2 3) STk> ((s1 'element-of-set?) 5) #f
since member is not a predicate [did you notice that the name does not end with ?]. We can still use the procedure in the same way as before because anything different than #f is considered true:STk> (let ((rest ((s1 'element-of-set?) 2))) (if rest (cdr rest) "notfound")) (3) STk> (let ((rest ((s1 'element-of-set?) 5))) (if rest (cdr rest) "notfound"))) "notfound"
- any more changes you can think of?
Week 9 - local state
This week we will start Chapter 3 and talk about how to change the value of a symbol (or a datastructure) in Scheme and how to write procedures that keep local state.Monday, March 19
- review of example of message passing for sets seen before the break.
- Pop quiz 6
You are given the following two (similar but not identical!) procedures(define (make-set-1 lst) (define (make-set-2 lst) (define (el-of-set x) (define (el-of-set x) (member x lst)) (member x lst)) (define (dispatch op) (define (dispatch op) (cond ((eq? op 'empty?) (cond ((eq? op 'empty?) (null? lst)) null?) ((eq? op 'element-of) ((eq? op 'element-of) (lambda (x)(el-of-set x))) el-of-set) (else "unknown op"))) (else "unknown op"))) dispatch) dispatch)and the following definitions:(define set1 (define set2 (make-set-1 (list 1 7 9 3))) (make-set-2 (list 1 7 9 3)))
Recall that (member el lst) returns the list starting at el if el is in the list and #f otherwise. Write Scheme expressions to:- check if set1 is empty
- check if set2 is empty
- find if 9 is an element of set1
- find if 9 is an element of set2
- set! is the Scheme instruction to modify the value of an existing variable.
- We start looking at the example from Chapter 3 on creating a bank
account:
;; use a global variable -- bad choice (define balance 100) (define (withdraw amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds")) ;; use a let and a lambda -- problemL we cannot create multiple copies (define new-withdraw (let ((balance 100)) (lambda (amount) (if (>= balance amount) (begin (set! balance (- balance amount)) balance) "Insufficient funds"))))
Wednesday, March 21
- use of set!
- more on bank account.
Friday, March 23
Week 10 - mutators
Monday, March 26
Practice and second quiz. Look at the solution.Wednesday, March 28
Guest lecture by Prof. Dovolis. Review of set!. Examples of set-car! and set-cdr!Friday, March 30
- example of message passing. Write a counter using message passing
style. A counter is an object with local state that is increment by 1
every time it is called. Here are two different solutions.
The first solution creates an object that does not take any message, but whenever called increments its counter by 1.(define (make-counter) (let ((counter 0)) (define (dispatch) (set! counter (1+ counter)) counter) dispatch)) STk> (define c1 (make-counter)) STk> (c1) 1 STk> (c1) 2The second solution takes two messages, one to increment the counter and one to return its value. This will allow reading the value of the counter without changing it.(define (make-counter2) (let ((counter 0)) (define (dispatch m) (cond ((eq? m 'value) counter) ((eq? m 'inc) (set! counter (1+ counter)) counter) (else "error -- unknown message"))) dispatch)) STk> (define c2 (make-counter2)) STk> (c1 'inc) 1 STk> (c1 'inc) 2 STk> (c1 'value) 2 - Pop quiz 7
Write a procedure (replace old new tree) to replace every occurrence of the element "old" in "tree" with "new". The procedure should work for trees (called also nested lists). If "old" is not in the tree, the procedure should return the tree unchanged. It should work like this:STk> (replace 'x '8 '(f x (+ y (f 1 x)))) (f 8 (+ y (f 1 8))) STk> (replace 'like 'dislike '(i (do not (like scheme)))) (i (do not (dislike scheme)))
Here are two solutions:(define (replace old new lst) (cond ((null? lst) ()) ((not (pair? lst)) (if (eq? lst old) new lst)) (else (cons (replace old new (car lst)) (replace old new (cdr lst)))))) (define (replace old new lst) (map (lambda (x) (cond ((not (pair? x)) (if (eq? x old) new x)) (else (replace old new x)))) lst))
Week 11 - tables
Monday, April 2
Wednesday, April 4
The table data structure.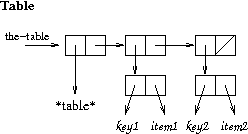
Friday, April 6
Pop Quiz 8Write a procedure (remove-2nd! lst) to remove the second element of a list. Assume the list contains at least two elements.
STk> (remove-2nd! '(a cold happy easter is coming)) (a happy easter is coming) STk> (remove-2nd! '(enjoy it)) (enjoy)Could you write a procedure to remove the first element of list? explain why or why not
Here is a solution that modifies the data structure (note the ! at the end of the procedure name).
(define (remove-2nd! lst) (set-cdr! lst (cddr lst)) lst)The figure shows the environment after the following:
STk> (define a '(a cold happy easter is coming)) a STk> (remove-2nd! a) (a happy easter is coming) STk> (remove-2nd! a) (a easter is coming)
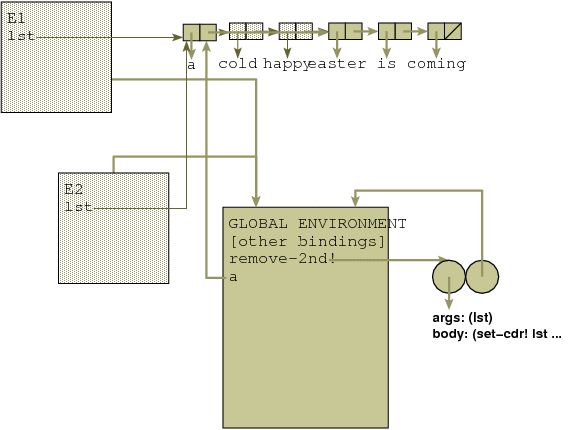
(define (remove-1st! lst) (set-car! lst (cadr lst)) (remove-2nd! lst))or directly
(define (remove-1st! lst) (set-car! lst (cadr lst)) (set-cdr! lst (cddr lst)) lst)
Week 12 - queues and agenda
Monday, April 9
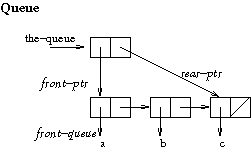
The queue data structure. What is a queue and how to implement it.- If we implement a queue as a list, with a pointer from head to tail, then it is easy to add elements to the end and to remove elements from the beginning. It is also easy (but slightly harder) to add elements at the beginning and remove elements from the end. The problem with either choice is that doing an operation at the end of the list requires traversing the list to reach the end and modify it. This makes the complexity of the operation linear in the length of the list, which is not desirable.
- To avoid the complexity issue we can save the pointer to the last
pair of the list, so we can get to it in one step. We need a place where
to store the pointer. We can add a cons box at the beginning of the list
and use it to store two pointers, one to the beginning of the list, and
one to the end of the list. This is the method commonly used for queues.
- We could instead represent the queue as an object that keeps its local state and responds to messages (see Exercise 3.22 on page 266).
set-car! and set-cdr!.
To understand how to write procedures to modify the data structure, make
a graphical representation of it, mark on it the pointers that need
to be changed, and write the corresponding scheme expression for
each change. Make sure your procedures are correct when the queue is
empty and when it becomes empty. You'll see in the procedures in the
textbook two cases, one for the empty queue and another for a non empty
queue. Try using ~boley/stk/runenvdraw to visualize the objects.
Wednesday, April 11
The agenda data structure and preparation for the AIBO lab.Look at the lecture notes for details.
Friday, April 13
More on the agenda. Recall that this is the data structure agenda.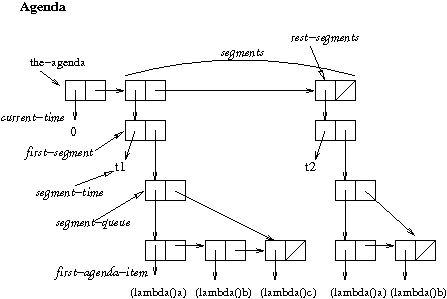
Pop Quiz 9
- Where does after-delay insert things?
- What's the difference between after-delay and add-action!
- Write a procedure to count how many actions are in an agenda
- How does propagate work?
Department of Computer Science and Engineering. All rights reserved.
Comments to: Maria Gini
Changes and corrections are in red.