Conveying the 3D Shape of Smoothly Curving Transparent Surfaces via Texture - IEEE Transactions on Visualization and Computer Graphics paper

Conveying the 3D Shape of Smoothly Curving Transparent Surfaces via Texture

Victoria Interrante
Institute for Computer Applications in Science and Engineering

Henry Fuchs and Stephen Pizer
University of North Carolina at Chapel Hill

ABSTRACT

Transparency can be a useful device for depicting multiple overlapping surfaces in a single image. The challenge is to render the transparent surfaces in such a way that their three-dimensional shape can be readily understood and their depth distance from underlying structures clearly perceived.

This paper describes our investigations into the use of sparsely-distributed discrete, opaque texture as an "artistic device" for more explicitly indicating the relative depth of a transparent surface and for communicating the essential features of its 3D shape in an intuitively meaningful and minimally occluding way. The driving application for this work is the visualization of layered surfaces in radiation therapy treatment planning data, and the technique is illustrated on transparent isointensity surfaces of radiation dose.

We describe the perceptual motivation and artistic inspiration for defining a stroke texture that is locally oriented in the direction of greatest normal curvature (and in which individual strokes are of a length proportional to the magnitude of the curvature in the direction they indicate), and discuss two alternative methods for applying this texture to isointensity surfaces defined in a volume.

We propose an experimental paradigm for objectively measuring observers' ability to judge the shape and depth of a layered transparent surface, in the course of a task relevant to the needs of radiotherapy treatment planning, and use this paradigm to evaluate the practical effectiveness of our approach through a controlled observer experiment based on images generated from actual clinical data.

1 INTRODUCTION

There are many potential advantages in using transparency to simultaneously depict multiple superimposed layers of information. The complex spatial relationship between two irregularly-shaped surfaces can be more easily understood when each surface is visible in the context of the other, and the three-dimensional structure of a scene can be more accurately and efficiently appreciated when the layered elements are displayed in their entirety, rather than having to be mentally reconstructed from an iterative sequence of 2D slices. However, in computer-generated images -- as in photographs and directly viewed objects -- it can often be difficult to adequately perceive the full three-dimensional shape of an external transparent surface, or to correctly judge its depth distance from arbitrary points on an underlying opaque structure. Although photorealism is a worthy goal, it does not, in and of itself, provide a complete solution to this problem: physically accurate rendering algorithms are difficult to implement and time-consuming to compute; faithfully depicting such phenomena as refraction and caustics may do more harm than good by introducing extraneous and distracting detail while confusing the perception of underlying information; and there is substantial evidence that photorealism is neither essential nor sufficient for clearly representing layered transparent surfaces. Transparency perception is only loosely constrained by the laws of optics -- it is fundamentally achromatic in nature [38], and readily perceived in a number of physically impossible situations [3, 14] while not perceived under other circumstances when it does exist in actuality [35]. Perhaps the most compelling argument for the insufficiency of photorealism, however, is the observation that the disciplines of medical and scientific illustration continue to flourish today, despite the advent of photography, precisely because it is so often the case that a photograph cannot adequately convey the necessary information about a subject or scene [32]. Through selective artistic enhancement we have the potential to portray information more clearly by minimizing extraneous detail and emphasizing important features [21].

The driving application for our work with transparent surfaces is radiation therapy, one of the three principal treatments for the control or cure of cancer. In radiation therapy, physicians attempt to eliminate cancer or alleviate its symptoms, while maintaining a high quality of life for the patient, by strategically delivering a high amount of radiation dose to targeted cancerous tissue while only minimally irradiating uninvolved areas. In planning a treatment, clinicians strive to define the number, orientation, shape and intensity of the multiple radiation beams to achieve a dose distribution that optimally balances the competing concerns of maximizing the probability of tumor control and minimizing the probability of normal tissue complications. This is a difficult and complicated task, requiring the tradeoff of many factors, both quantifiable and unquantifiable. We may help facilitate the treatment planning process by devising a means of more effectively portraying the three-dimensional distribution of radiation dose in the context of the relevant patient anatomy.

2 SHAPE AND DEPTH CUES ON TRANSPARENT SURFACES

In determining how to best enhance the comprehensibility of transparent surfaces in computer-generated images, it is useful to begin by looking at some of the underlying explanations for the difficulties that we often encounter in perceiving the shapes and relative depths of layered transparent surfaces in everyday experience.

Figure 1 shows, for reference, some example photographs of actual transparent objects. Although the shapes of these depicted objects are far more regular and predictable than the shapes of the isodose surfaces we aim to represent, the lack of naturally-occurring shape and depth cues on the front-facing portions of these realistically rendered plain and smooth transparent surfaces is nevertheless quite striking. Specular highlights, environmental reflections and refractive distortion provide the only potential sources of surface shape information, and surface depth information is almost completely unavailable.

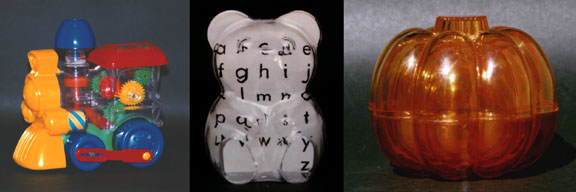
Figure 1: Photographs of actual transparent objects, indicating the paucity of naturally occurring shape and depth cues. Left: a plastic train with see-through chassis; center: a plastic bear superimposed over an alphabet flashcard; right: a set of three nested pumpkins.

2.1 Silhouettes and contours

Most of the shape information available in photographs of clear, transparent surfaces is contained in the silhouette and contour regions. Silhouettes are important for form perception because they define the boundary between figure and ground, and contours, defined as the locus of all points where the surface normal is orthogonal to the viewing direction [25], mark both internal and external depth discontinuities. Although we are able to infer the nature of the 3D shape of a closed surface in the vicinity of an occluding contour from the sign of the curvature of the contour (convex contours indicate areas of positive Gaussian curvature, concave contours indicate hyperbolic regions, and locally flat points or inflections indicate a parabolic line or a region of zero Gaussian curvature [44]), these contour curves provide little indication of depth distance or surface shape across forward-facing areas. The effects of refraction, which are most strongly evident where the viewing direction grazes the surface, can sometimes emphasize silhouettes and contours, and perhaps indirectly indicate some curvature features of an external transparent surface, but these small gains come at the expense of potentially significant distortion of interior or rearward structures. Because we aim to communicate the shapes and relative distances between multiple layered surfaces, it is important to provide as clear a view of each structure as possible. Therefore we have chosen not to model the effects of refraction but to rely on luminance or color differences to convey figure/ground discontinuities.

2.2 Shape and depth from shading

Shape- from- diffuse shading cues are minimal at best on clear, transparent surfaces, and occlusion, normally one of the most powerful indicators of depth order relations, is present only to the extent that the intensity of a reflected light precludes the discrimination of underlying entities. Specular highlights and environmental reflections can provide some cues to surface shape, but, because they are viewpoint-dependent, they cannot provide an accurate indication of the relative depth of a transparent surface, in either a monocular or binocular view.

As an object is repositioned or the viewing direction changed, the apparent locations of the specular highlights will shift about. Specular highlights move more slowly over highly curved regions, tending to cling to ridges and valleys [24]. When both the viewpoint and the light source are sufficiently distant from the surface, so that in the case of a concave surface the caustic sheets defined by the envelope of reflected rays lie between the eye and the surface, it is possible, in the vicinity of a specular highlight, to infer the sign of the surface curvature in the direction of known object or observer motion from the direction of the relative motion of the specular highlight [4, 61]: in convex or nearly planar areas, a specular highlight will move with a moving observer; in concave regions, the directions of these motions will usually¹ be opposed; the direction of motion of a specular highlight across a hyperbolic surface will depend upon the orientation of the surface relative to the direction of the observer motion. However, the extent of this motion can be reliably perceived only in the presence of fixed surface detail, and the direction of this motion promises to be useful only, when the magnitude of the surface curvature is reasonably significant, for disambiguating convex from concave patches. Little depth information is available from the velocity gradients of specular highlights under conditions of object or observer motion, either with respect to other surface features or with respect to specific points on an underlying opaque object.

When a shiny object is observed with both eyes, the specular highlights will appear to lie in different locations on the surface in the view from each eye (it is easiest to see this with a point light source and an opaque, textured object). Because the retinal disparity of the specular highlights differs from the retinal disparity of the surface detail in the corresponding views, the highlight will be perceived to be located at a different distance from the viewpoint than the surface. Blake and Bülthoff [4] describe how specular highlights will usually appear to float slightly behind convex surfaces and slightly in front of concave ones, and figure 2, after diagrams and discussion in [4], illustrates the geometric principles behind this phenomenon, for the case of a spherical object and a distant light source.

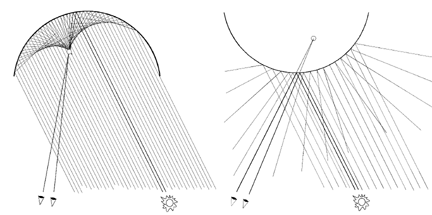
Figure 2: This diagram, modeled after images and discussion in Blake and Bülthoff [4], demonstrates why specular highlights will generally appear to float behind convex surfaces and in front of concave ones.

The extent of the apparent offset between a surface and its specular highlight will be a function of both the magnitude of the surface curvature in the direction of the retinal disparity and the distance of the surface from the viewpoint. Although psychophysical evidence indicates that people can learn to disambiguate convex from concave surfaces from the differences in the direction of the depth disparity of the specular highlight in these two cases [4], the existence of this depth disparity implies that specular highlights cannot be assumed to meaningfully indicate surface depth in a stereo view.

2.3    Shape and depth from sparse, opaque texture

Much of the difficulty that we have in perceiving the relative depth of an overlaid transparent surface can be attributed to the absence of easily-detectable stable surface features that would allow stereo fusion at correct depth distances and provide reliable monocular cues to depth through motion. Although some shape information is potentially available from the patterns of motion and relative disparity of specular highlights, these indications of shape are isolated, incomplete, and arguably less-than-immediately intuitive in the course of casual inspection. There are a number of reasons, therefore, to believe that we might be able to facilitate the perception of both surface shape and depth by artificially enhancing an external transparent surface with a small, fixed set of appropriately-defined opaque "texture" elements. Psychophysical experiments indicate that observers perceive more depth in images in which multiple complementary cues indicate similar depth information [6]; rather than being redundant, these repeated indications of depth appear to reinforce each other, strengthening the overall perception of depth in the image [60]. By fixing an evenly-distributed, sparse opaque texture to an otherwise plain transparent surface, we may specify its three-dimensional location more explicitly and completely while preserving the visibility of underlying structures, provide stable occlusion cues, facilitate the veridical perception of surface depth from binocular disparity, and enable an intuitive perception of shape and depth from the velocity gradients of fixed surface points. By carefully defining the texture to convey essential shape features in a perceptually intuitive and minimally occluding way, we may further facilitate the perception of both surface shape and depth by enabling a rapid, global appreciation of the essential shape characteristics of the external transparent surface and facilitating an intuition of its relative depth at points not marked by texture.

3    PREVIOUS WORK

In an earlier paper [23], we suggested that the essential shape features of certain familiar transparent objects might be communicated particularly effectively via a rendering approach intended to approximate the style of a "3D, view-independent sketch", in which the valley lines and the crests of sharp ridges are selectively emphasized by being displayed with greater opacity than other, less strategically significant surface regions. Although this approach yielded promising results on some of the transparent skin surfaces that it was designed to represent, we immediately recognized that not all of the surfaces in our layered treatment planning data would be easily characterizable by prominent, shape-based features. A different approach was needed for conveying the shapes and depths of the smoothly undulating, vaguely spherical, layered isointensity surfaces of radiation dose -- an approach that relied on a more evenly-distributed set of sparse opaque markings.

It has long been recognized that the slant of a flat plane or the shape of a smoothly curving surface can be conveyed much more effectively when the surface is textured rather than left plain [12, 50, 54], and although there appears to be no definitive agreement on the specific characteristics of a texture pattern that are most instrumental in indicating shape, this question has been repeatedly broached in the visual perception literature [15, 12, 10, 51, 55, 56, 9]. The idea of using opacity-modulating texture to enhance the visibility of layered transparent surfaces is also not new. Three general approaches have been previously proposed: Dooley and Cohen [11] suggested using a fixed screen-space pattern to modulate the opacity of a transparent surface after projection onto the image plane; Levoy et al. [29] used a uniform sampling of finite-width planes along the three orthogonal axes of a 3D dataset to define a volume opacity mask that could be applied as a generic "solid texture" [40] during volume rendering; and Rheingans [43] developed a method for using standard hardware texture-mapping routines to apply a procedurally-defined 2D texture across evenly-distributed points on an arbitrary surface in 3D. In addition, there is significant precedent, particularly in applications that use computer graphics for interactive data display, for representing a continuous transparent or opaque surface by a sparse set of discrete graphical primitives such as points, lines, spheres, or triangle strips [8, 41, 45, 1]. Sometimes intended more as a means of improving rendering efficiency than as a device for improving the comprehensibility of surface shape, it can be argued that the best of these methods serve both purposes well.

The particular contribution of the work presented in this paper is to suggest that the shape and depth of a gently curving, layered transparent surface may be communicated particularly effectively via a relatively evenly-distributed, sparse opaque texture that has been explicitly designed to convey basic surface shape properties in a perceptually intuitive and minimally occluding way. The method that we propose was inspired by observations of artists' use of line to show shape and is based on fundamental concepts from differential geometry.

4    ARTISTS' USE OF TEXTURE TO COMMUNICATE SURFACE SHAPE IN LINE DRAWINGS

Our central premise in this work is that there is a definable art to effectively conveying shape with line. Although it has been experimentally demonstrated that observers can fairly accurately recover the local surface orientation at a selected surface point from the apparent slant and tilt of a circular element at that location [52, 2], medical and scientific illustrators rarely use such markings in their work. Recent psychophysical research suggests that shape is internally represented as an organization of space, based on local depth order relations, and not derived from individual estimations of the direction of the surface normal at distributed points [56, 26]. Artists caution against representing strokes, or any texture elements, in such a way that they take on a character of their own, noting that when individual texture markings are unduly prominent, they often do more harm than good, distracting the attention of the observer, confusing the appearance of the picture and adding visual noise that detracts from rather than enhances the overall effectiveness of the presentation.

When artists and illustrators represent a 3D form in a 2D, static line drawing, they appear to rely primarily on line width and spacing to specify shape via shading, and on stroke direction to describe the structural "flow" of the form. Foreseeing a number of potential difficulties with gracefully depicting changing patterns of surface illumination via continuous texture modifications under conditions of dynamic viewing, we have chosen to side-step this issue for the moment and restrict ourselves to the pursuit of a viewpoint- independent texture representation based on stroke direction, leaving shape-from-shading cues to be provided by the illuminance distribution across the opaque texture elements.

Artists have repeatedly emphasized the importance of stroke direction in line drawings [53, 42, 18], and it is popularly recognized that our perception of a surface's form will be significantly affected by the direction of the lines that are used to represent it. Figure 3, reprinted with permission from a 1957 text on ink drawing techniques by Henry C. Pitz [42], was designed to demonstrate the consequences of various different approaches to defining line direction. Pitz states that:

Horizontal lines tend to make things wider; vertical lines make them seem taller... Lines following the contour of a surface emphasize that surface; haphazard lines tend to destroy the integrity of the surface.

Figure 3: An illustration of the effects of line direction on object appearance. Henry C. Pitz, Ink Drawing Techniques, ©Watson-Guptill Publications, 1957.

When strokes are applied in a uniform fashion across an entire image, objects will tend to appear flattened. Guptill [18] advises that "as a general rule, a subject offers some hint as to a natural arrangement of lines", but references to specific algorithms for defining a line's direction so that it follows the form over which is laid prove to be somewhat elusive. In one of the few texts that offer a detailed treatment of this subject, Sullivan [53], also recommending that "it is a good general rule to make any group of lines used for the modelling of a surface follow the form, on some simple scheme", suggests two alternative methods for defining stroke direction. The simplest of these he describes as "guided by the fall of light upon the object", which can be represented as the projection of conical arcs or radial lines emanating from a point light source at close proximity to the subject. However, he cautions that this approach may have a flattening effect where the orientation of the strokes closely parallels the boundary of the form. The second method, which he describes as "probably the most difficult ..., based more strictly upon the form itself and demanding the greatest knowledge of it", is to align the strokes at "right angles to the length of the form". If one assumes that the "length" of a form is described by the direction of least surface curvature, this can be alternatively interpreted as corresponding to the direction of the strongest curvature of the surface, or the first principal curvature.

Medical illustrators, in particular, appear to favor a form-following convention for using line to depict surface shape, as indicated by the two representative examples reprinted in figure 4. The image on the left won an Honorable Mention in the Medical Line category in 1990, and the image on the right, by the late Russell Drake (one of the masters in this field), has been cited as an excellent example of his classic single line technique of shading. It is crucial to note the quality of the lines that are used to represent form in these images. They are neither random nor uniform in direction, but have been insightfully chosen to emphasize surface shape in a clear and intuitive way.

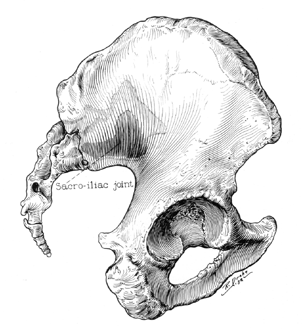
Figure 4: Representative examples of the use of line in medical illustration. Left: "Surgical Repair of Septate Uterus, Figure A", by John V. Hagen, in Atlas of Gynecologic Surgery, Raymond A. Lee, Saunders, Philadelphia, 1992. ©Mayo Foundation. Right: "Lumbosacral and Sacroiliac Fusion", Russell Drake, medical illustrator, Mayo Foundation, 1932.

5 PRINCIPAL DIRECTIONS AND PRINCIPAL CURVATURES

In order to represent the curvature of a form with stroke direction, it is necessary to first define a means for extracting this geometric information, and to do this we turn to the classic mathematical descriptions of surface shape provided by differential geometry [20, 25].

At any non-spherical point on a generic, smooth surface there will be a single direction, orthogonal to the surface normal, in which the absolute value of the surface's normal curvature is greatest (normal curvature is defined in any particular direction by the curvature of the strip of the surface that intersects the plane spanned by the normal and the specified direction vector). This direction, in which the surface is curving most strongly, is referred to as the first principal direction, and the curvature in this direction is referred to as the first principal curvature. The second principal direction, which also lies in the tangent plane and is always orthogonal to the first principal direction, specifies the direction in which the surface is flattest. Figure 5 shows the principal directions and the corresponding curvature strips at a typical point on a hyperbolic surface patch. The principal curvatures are of opposite signs in this case. The principal directions and principal curvatures can be easily computed at arbitrary points on a smoothly curving surface from the eigenvectors and eigenvalues of the second fundamental form [25, 37]. Monga et al. [36] describe an efficient algorithm for obtaining principal curvatures on isointensity surfaces in volume data directly from the first and second derivatives of the intensity information and without any local surface fitting.

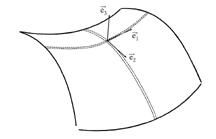
Figure 5: Curvature strips in the principal directions at a point on a hyperbolic patch.

For the particular application described in this paper, we will only need to compute principal directions and principal curvatures at a relatively small number of predetermined points. We begin by defining an orthogonal frame, (e₁, e₂, e₃) at the selected surface point P_xyz, where e₃ points in the surface normal direction and e₁ and e₂ span the tangent plane (we obtain e₁ by choosing an arbitrary direction in the tangent plane, and then derive e₂ by taking the cross product of e₁ and e₃). From this orthogonal frame we can determine the Second Fundamental Form

A = [ w₁¹³ w₁²³
w₂¹³ w₂²³ ]

a matrix that describes the local surface shape in terms of the tangent planes in the local neighborhood of P_xyz. The coefficients w_jⁱ³ specify the component in the e_i direction of the rate at which the surface normal tips as you move across the surface in the e_j direction; when i=j these terms have been described as specifying the nose-dives of the frame, and when i<>j as specifying the twists [25]. We compute w_jⁱ³ in practice by taking the dot product of e_i and the first derivative of the gradient in the e_j direction. It is essential to use floating point values for the gradients, and smoother results are achieved when the data is prefiltered, or when instead of using simple central differences, a Gaussian-weighted derivative operator is applied over all of the voxels in the local 3x3x3 neighborhood. The twist terms w₂¹³ and w₁²³ need to be equal. The next step is to rotate the orthogonal frame about e₃ so that the twist terms disappear by diagonalizing A to obtain

D = [ k₁ 0
0 k₂ ] , and P = [ v_1u v_2u
v_1v v_2v ]

where A = PDP^-1 and |k₁| > |k₂|. The principal directions in R³ are given by e_i' = v_iu e₁ + v_iv e₂, and the principal curvatures are specified by k₁ and k₂. Though all of this may sound a bit complicated, we have found in practice that it takes only a few seconds to perform a very straightforward implementation of these calculations on the handful of selected points where we need to know this information.

6 RELATED WORK

The idea that we might effectively communicate surface shape by explicitly representing the principal directions and principal curvatures on a surface has precedents. Frobin and Hierholzer [13] used a local surface-fitting approach to define the principal directions and principal curvatures at evenly-spaced points on discretely sampled, acquired height data of the human back, and demonstrated how these quantities could be displayed as a pattern of cross hairs on a 2D grid. Their goal was to convey position-invariant surface shape information not easily accessible from the then-standard Moire topograms. Researchers in computer vision also pursued the idea that an intrinsic surface description could be assembled from local differential geometry measurements computed on surfaces in acquired data. Brady et al. [5] proposed an approach wherein local estimates of the directions of principal curvature were "linked" across a surface and planar "lines of curvature" extracted, and Sander and Zucker [49] computed principal direction vectors on surfaces in three-dimensional data as part of their efforts to derive an analytical surface representation and to define and categorize its various patches according to the properties of their Gaussian curvature. Researchers in computer-aided design, who are working primarily with analytically-defined surfaces, have developed a number of sophisticated methods, based on concepts from differential geometry, for detecting and depicting a wide variety of important surface shape properties [19, 17, 37]. Collectively referred to as surface interrogation techniques, these methods include: using lines of constant illumination called isophotes to reveal the degree of curvature continuity across a surface region (if a surface is C^r continuous, the isophotes will have C^r-1 continuity); using the pattern of reflection of parallel light lines to reveal irregularities in surface curvature (a standard technique in auto manufacturing); using color-coded maps of Gaussian curvature, mean curvature, minimum or maximum principal curvature, and lines of constant curvature to help define optimal tool sizes and paths for numerically-controlled milling [34]; computing and displaying offset surfaces, focal surfaces, orthotomics, "contour" curves formed by the intersection of the surface with a series of planes along an arbitrary axis (this use of the term contour in this context should not be confused with the use of the same term in section 2.1 to refer to a completely different entity) and more. Guid et al. [17] assert, however, that "displaying the directions of principal curvatures on a regular grid stretched over the whole surface...give[s] a user nearly no information", and there are few indications that such an approach has many followers in this particular field.

The goal of artistically representing surface shape with line has inspired some very fine techniques for automatically generating line-drawings that bear a remarkable resemblance to the work of pen-and-ink artists. Although these techniques don't involve principal directions, and are thus far only applicable on planar or parametrically-defined surface patches, we mention them here because the results are so very inspiring. Saito and Takahashi [46] did some of the earliest work in this area, defining a hachuring pattern based on the surface parameterization of a torus and applying it in proportion to the surface shading indicated by an illumination map. It is important to note that although in this particular case the lines of the parametric representation fortuitously coincide with the principal directions, such a correspondence cannot be expected to hold under general circumstances. Winkenbach and Salesin first described methods for automatically generating pen-and-ink style renderings of architectural models in which resolution- independent stroke textures were applied to planar surfaces [58], and then later extended this work to apply similarly-detailed stroke textures to parametrically-defined surfaces, following the direction of the parameterization [59]. They suggest the possibility of using principal directions, in future work, to guide the placement of strokes on non- parametrically defined surfaces. Salisbury et al. created an interactive pen-and-ink style drawing program in which, among other things, the orientation of the individual elements of a higher-level stroke could be specified to follow the direction of the intensity gradient in a two-dimensional reference image [47], and then later extended this work by proposing a resolution-independent technique for storing and reproducing pen-and-ink illustrations at arbitrary scales and sizes [48].

7 DEFINING A PRINCIPAL DIRECTION TEXTURE

There are three principal considerations in defining a texture of distributed, opaque strokes that can effectively convey the essential shape properties of an external transparent surface while preserving the visibility of underlying structures. The first, and most important, is stroke direction, which we define to be aligned with the first principal direction.

A second consideration is stroke placement. Given the needs of our application, we could foresee several potential pitfalls and no particular advantages to varying the clustering density of the texture strokes according to either shading or curvature properties, and we therefore chose to center the strokes at an evenly-distributed subset of the points defined by the vertices of a marching-cubes [33] triangulation of the isosurface being represented. The algorithm that we use to select the stroke centerpoints accepts as input a list of triangle vertices and through an iterative process generates a sublist of vertices in which no two entries are closer than a user-specified Euclidean distance in three-space. Although standard solid texturing algorithms, which employ textures that are defined independently of any particular surface, do not require such a step and can be somewhat simpler to define, easier to render and more flexible in terms of being applicable to an arbitrary number of different level surfaces in a given volume, it is difficult to explicitly portray specific surface shape features using such methods.

The third issue is the definition of stroke length and width. Although line width, as well as spacing, might potentially be used to reinforce shape-from-shading information, adopting such an approach would mean sacrificing the viewpoint-independence of the texture representation. We have therefore elected to use a single, common value for stroke width across an entire surface in this implementation. Appropriately selecting the stroke length, however, turns out to be of suprisingly crucial importance. The reason for this is that not all of the principal directions that we have computed are equally important for shape understanding. Where a surface is relatively flat, tiny irregularities can have an unduly large influence on the computed direction of locally maximum surface curvature, and small errors in surface normal calculations, due for example to inadequate smoothness in the implicit reconstruction of the discretely sampled data, can have a magnified deleterious impact on the accuracy and consistency of the computed principal directions at those points. Because the length of each stroke directly determines the visual impact of the direction that it defines, it is essential to define stroke length in such a way that specific directions are most strongly indicated in the surface regions where their particular values are of greatest perceptual importance. By tying the length of a stroke to the magnitude of the first principal curvature, we ensure that stroke length is minimal in particularly flat areas, where there is less justification for emphasizing one particular direction over all others, while at the same time allowing directional information to be prominently represented across strongly curved surface regions. Although it can be argued that directional ambiguity is potentially as much of a problem in locally spherical areas as it is in places where the surface is locally flat, the use of longer strokes may be more easily justified in the former case, where the longer lines seem more capable of aptly conveying the rapidly changing nature of the surface orientation. Figure 6 shows examples of the kinds of results that we are able to achieve in applying a principal direction stroke texture to transparent isointensity surfaces of radiation dose, enclosing opaque treatment regions, in a variety of different datasets. For clarity, we have adopted a rendering style in which only the foremost layer of the external surface is made visible in each of these images.

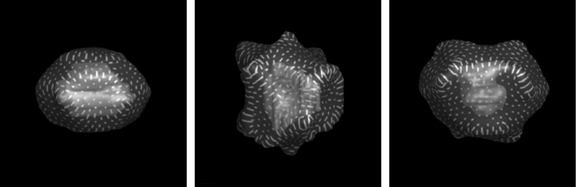
Figure 6: Principal direction texture applied to several different transparent isointensity surfaces of radiation dose, surrounding opaque treatment regions.

Figure 7 illustrates the effect on surface representation when stroke length is allowed to remain constant.

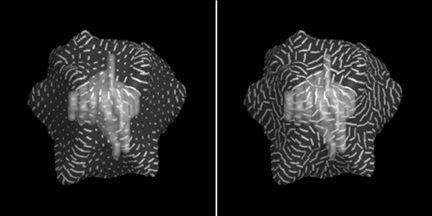
Figure 7: An illustration of the importance of defining stroke length according to the perceptual relevance of the directions they indicate. Left: texture element length is proportional to the magnitude of the normal curvature in the stroke direction; right: element length is constant.

7.1 Modelling the individual strokes

Our driving application requires the simultaneous depiction of multiple superimposed surfaces defined from volume data, and the method that we use for implementing a principal direction texture is rooted in the framework of the raycasting volume renderer [30] that we have historically used to make images of 3D radiotherapy data. Individual strokes are modelled as polygonally-bound solid slabs whose areas of intersection with the transparent isodose surface define the specific surface regions that will be rendered with increased opacity. Figure 8 illustrates the stroke modelling process. The corner vertices of each 3D slab are specified by the points v_x,y,z = ( p_x ± le₁, p_y ± we₂, p_z ± he₃ ), where p_x, p_y, and p_z define the location of centerpoint P, l, w, and h specify the half-length, half-width and half-height of the slab, and e₁, e₂, and e₃ are the unit vectors that define the principal frame: e₁ corresponds to the first principal direction, e₂ corresponds to the second principal direction, and e₃ is aligned with the direction of the surface normal at P.

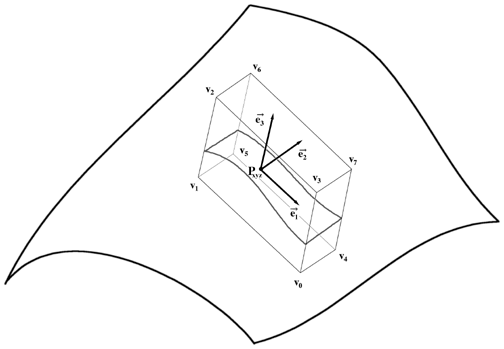
Figure 8: An illustration of the procedure for defining a principal direction stroke around a selected point on a curved surface.

The value of h, a user-specified constant, should ideally be large enough so that each slab will contain the surface across its fullest possible extent but not so large that it will cause the surface to be opacified in unintended areas. Although it is obviously possible to imagine situations in which it would be impossible to come up with a value of h that neither excessively truncates strokes across the tops of sharp ridges nor generates unwanted opacification in areas where the surface nearly folds upon itself, we have not encountered any such difficulties in practice. If such a situation were to arise, it would be more appropriate to use an adaptively determined value for h. The value of w, another user-specified constant, can be defined to be arbitrarily small, and it is certainly the case in general that thinner strokes will be less visually distracting and can be expected to evoke a more intuitive impression of a gently-textured curving form. We have found that it is difficult to get clear results, however, when w falls below about 0.35 of the distance between adjacent sampling rays. The value of l is defined independently for each stroke, and is locally determined by MAX(w,l₀k ), where l₀ is a constant specified by the user to bound the maximum possible stroke length and k = MIN(|k₁/k_max|, 1) indicates the relative magnitude of the curvature of the surface in the slab direction: k₁ is the value of the first principal curvature at the slab centerpoint, and k_max is a scaling factor that approximates the maximum of the magnitudes of the principal curvatures over all points on the isovalue surface. Because the strokes are modelled as straight slabs, the fidelity with which the displayed stroke direction matches the direction of a line of curvature will degrade toward the ends of the stroke, and it is necessary to keep the maximum stroke length reasonably short. By modelling a larger number of shorter strokes rather than a fewer number of longer strokes we are able to keep the texture definition process simple and local.

Although there is a fair amount of latitude possible in the specification of the various parameters defining inter-element spacing, element width, maximum element length and element length scaling, we did not find it particularly profitable to exhaustively search the values of these parameters in pursuit of an "optimal" combination. In general, we found thinner strokes to be preferable to thicker strokes (as long as the strokes were not so thin that they occupied only a fraction of the width of a display pixel), and favored setting the minimum inter-element distance to a value large enough to avoid as much as possible having multiple slabs overlap each other. Additionally, we found after a time that it was not actually necessary to precompute all of the principal curvatures and determine their maximum in order to select an appropriate quantity for k_max; although it is useful to have this information, the overall quality of the results do not seem to be particularly sensitive to the value of this parameter and we were able to achieve very reasonable-looking images for a number of different surfaces using a single estimate of k_max, chosen a priori.

7.2 Applying the texture to the surface

Once the stroke geometry has been defined, there are two basic options for applying them to the surface during rendering.

The first approach we tried was to scan-convert the polygonally-defined texture slabs into a grey-scale volume that could be applied as a solid texture to selectively increase the opacity of corresponding points on the transparent isovalue surface. To perform the scan conversion without introducing significant aliasing artifacts, we computed the binary occupancy of each of the 64 subvoxels in a 4x4x4 super-sampled version of the solid slab data, and then averaged the results to get a byte value capable of adequately representing partial occupancy. The primary advantage to this technique was that, after the expensive overhead of the scan conversion, we were able to reuse the volume opacity mask to quickly generate multiple images of a particular textured surface from different orientations. The primary disadvantage to this approach, and the reason that we eventually chose not to use it, was that the fidelity with which we were able to represent fine stroke textures was fundamentally limited by the relatively coarse resolution of the volume data. In subsequent side-by-side comparisons with the alternative approach described below, it became apparent that the crispness of the individual strokes in the final renderings was being compromised by this intermediate discretization step.

To address the problem of achieving thinner, sharper lines we turned to a second method for applying the principal direction texture. In this approach, we pass the geometrical definition of the individual stroke slabs to the volume rendering program and, during raycasting, keep track of the intersections of each ray with the polygons bounding each slab. In this way we can simply and accurately determine to sub-voxel accuracy whether any given ray/surface intersection point lies within an opacifying slab. By tagging each of the slab polygons with a label indicating the identity of the slab to which it belongs, we are able to gracefully handle the case of intersecting slabs and more robustly check for errors that can infrequently arise when for one or another reason an odd number of ray/slab intersections is detected. The primary disadvantage of this approach is that testing for all possible intersections of each viewing ray with every one of the slab-bounding polygons is expensive, and these tests have to be repeated for each successive view in a moving sequence.

Figure 9: A side-by-side comparison of the two stroke representation methods. Strokes are specified geometrically in the image on the left, and scan-converted in the image on the right.

Our main concern in this work was with the issues of texture design, and we do not wish to suggest that we believe that the particular implementations described above are optimal. However, they are extremely straightforward, and although we did not attempt such an endeavor, we believe that a number of different techniques [16] can be used to improve their computational efficiency.

8 RESULTS

8.1 The visual impact of principal direction textures

Figure 10 provides additional insight into the potential usefulness of principal direction texturing for conveying the shape of an external surface while maintaining the visibility of internal objects by showing a single pair of dose/volume surfaces rendered in three different ways. In the image on the left, the dose is represented by a plain transparent surface. Although the view of the underlying target volume is very clear, the shape of the outer surface cannot be readily perceived, and there are few available cues to the magnitude of the depth distance between these two surfaces. The image in the center shows what the external surface looks like when it is rendered with full opacity. On the right the surface is shown with principal direction texturing. The essential shape structure of the external isodose surface is represented by the strong indication of the four main ridges across its front-facing region, while the details of the interior can still be easily seen. When this data is rotated, or viewed in stereo, numerous cues to the depth distance between the internal and external surfaces become available.

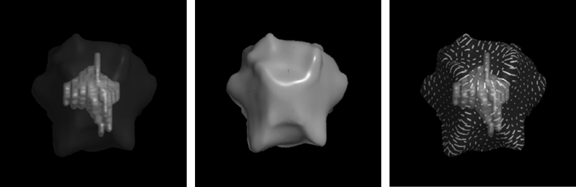
Figure 10: Different views of a set of layered dose/target surfaces. Left: transparent outer shell. Center: opaque outer shell. Right: transparent outer shell with opaque principal direction texture.

8.2 Empirical comparisons with other approaches

An objective determination of the relative merits of adding a principal direction texture to a transparent surface, as opposed to adding no texture or using an alternative texture definition, needs to be based on controlled observer experiments that quantitatively measure the ability of subjects to make shape and depth judgements that depend on a simultaneous understanding of the shapes and relative depths of the layered surfaces, and such an experiment is described in section 9 of this paper. However, useful insights into the relative merits of principal direction texturing may potentially be gained from empirical comparison with a wider variety of texturing methods than those considered in this experiment. In figure 11, we illustrate a variety of alternative methods for texturing a transparent surface with sparsely distributed opaque markings. To facilitate comparison, the surfaces shown here are all identical, and are the same surfaces as shown in figure 10. To appreciate the differences in the quality of the shape description provided by these different texturing methods, it may be helpful to try to imagine how easy or difficult it would be to faithfully reproduce a 3D model of the depicted surfaces, for example in clay, solely from the information available in each of the images.

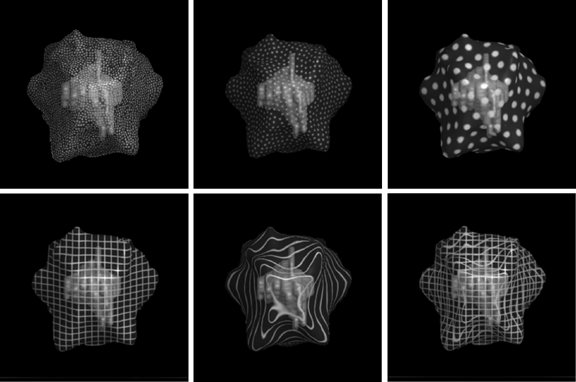
Figure 11: Alternative methods for texturing a transparent surface with sparsely-distributed opaque markings. Each of these images depicts the same dataset. Upper row: spot textures of various sizes and spacings. Lower left: grid lines generated by the intersection of the outer surface with planes evenly spaced along two orthogonal axes, perpendicular to the viewing direction. Lower middle: grid lines generated by planes evenly spaced along the axis of the viewing direction. Lower right: grid lines generated by planes along the three orthogonal axes of the data volume.

The pictures in the top row of figure 11 show spot textures of different element sizes and spacings. The spots in each of these images were defined to lie at evenly- distributed points over the external transparent surface. Under conditions of stereo and/or motion, appreciation of the inter-surface distances is facilitated by the explicit indication of the presence of the outer surface at the location of each spot. As spot size increases, the particular projective deformation of each individual spot becomes easier to discriminate, allowing the amount of surface slant at the spot center to be more readily appreciated. However, as the opaque material becomes more tightly clumped and the spacing between elements increases, the perceptibility of subtle local luminance gradients is impeded and shape-from-shading information is no longer as easily extracted. In the top left image, almost all of the available shape information comes from the shading of the spots; in the top right image, almost all of the available shape information comes from the projective deformation of the circular texture elements. In the intermediate image, shape-from- shading and shape-from-texture cues are each present, but to less of an extent individually than in the respective neighboring representations. The "essential features" of the surface shape, the four opposing ridges that merge in the central plateau, are not clearly indicated in any of these depictions.

The lower left image in figure 11 shows a grid texture formed by the lines of intersection of the surface with two sets of parallel planes, evenly spaced along the two orthogonal axes of the data volume most nearly aligned with the image plane [29]. The principal advantage to this representation is its ease of definition. Unlike surface-specific methods, in which individual texture elements are placed at predetermined points across a predefined object, this method relies on an even spacing of elements in the 3D volume, independent of the surface location. Thus a single predefined grid can be applied to any arbitrary surface. However, the resulting line pattern seems to offer few immediately intuitive cues to shape from texture, and shape-from-shading cues are relatively difficult to discern. Perception of the outer-to-inner surface distances is greatly facilitated, however, when the data is viewed in stereo or in motion.

The central image in the bottom row of figure 11 shows a contour line texture highlighting the intersection of the surface with a series of scan-converted parallel planes evenly spaced in depth along the viewing direction. It is possible to deduce both shape and depth information from the pattern of lines in this representation. However, the specific surface characterization provided in any single view will be extremely sensitive both to the phase of the texture and to the particular location of the vantage point. Special precautions often need to be taken to avoid allowing relatively flat front-facing patches of the surface to coincide with the thickness of a scan-converted plane. A third option, shown in the lower right image of figure 11, is to define a solid grid texture along all three orthogonal axes of the data volume. Such a representation will be both viewpoint and surface independent, but shape features remain only indirectly expressed and it is difficult to argue that such a representation allows an immediate, intuitive appreciation of the shape character of the external transparent surface.

8.3 The complementary roles of stroke direction and lighting

The shape information conveyed by the pattern of stroke directions and lengths in a principal direction texture is complemented by the shape information conveyed by the distribution of illumination over the elements. As can be seen from figure 12, a surface's shape may be most easily understood when lighting and stroke direction/length cues are both present, and is somewhat less comprehensible when either of these cues is absent.

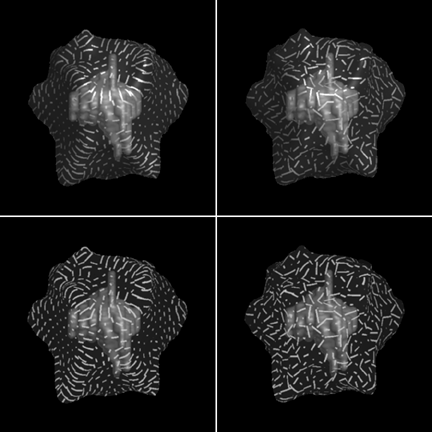
Figure 12: An illustration of the complementary roles that curvature-defined stroke characteristics (direction and length) and texture element illumination play in conveying surface shape. Upper left: shaded, directionally-oriented strokes of length proportional to curvature in the stroke direction. Upper right: shaded, randomly-oriented strokes of randomly-determined length. Lower left: unshaded principal direction strokes. Lower right: unshaded random strokes.

8.4 The role of color

Abundant psychophysical evidence indicates that shape and depth perception are almost entirely mediated by the luminance channels in the human visual system [31]; the perception of shape and depth from shading and shadows has been specifically shown to be largely independent of hue [7]. Given this understanding, we do not foresee any significant advantage, for this particular application, in attempting to use color to intuitively convey specific surface shape information.

The most useful role for color in this application will be as a labelling device, either to clarify the distinct identities of the depth-separated points on the multiple layered surfaces or to encode a specifically relevant third variable, such as the depth distance from any point on the outer surface to the closest point on the inner, as demonstrated in figure 13.

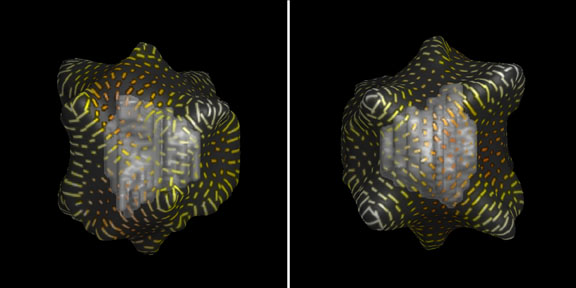
Figure 13: The color of the principal direction texture strokes in these images is defined to reflect the magnitude of the shortest distance from the outer to the inner surface at each point.

8.5 Multiple transparent layers

So far, we have only considered the case of two overlapping surfaces (one transparent layer). The introduction of an additional transparent layer raises a number of new issues, and it's not clear how well any of the texturing methods we have considered would generalize to this situation. Probably one of the most critical problems in using texture to characterize surface shape in the case of multiple superimposed transparent layers is the problem of texture segregation. Observers must be able to easily differentiate between the texture elements that indicate each distinct surface, in both a global and a local context, and to selectively direct attention, via perceptual grouping, to all of the elements belonging to each individual layer. Perceptual grouping will be facilitated under conditions of stereo and motion by the introduction of depth discontinuity and common fate cues, but preliminary investigations indicate that color differences alone are not sufficient to allow the effortless disambiguation of layered principal direction textured transparent surfaces in a static image. Figure 14 shows the kind of effect that is achieved when each of two overlapping transparent surfaces are textured with principal direction strokes of different colors. Haloing the individual texture elements to indicate depth discontinuity information helps somewhat, but it is clear that additional measures are necessary to satisfactorily differentiate the two layers.

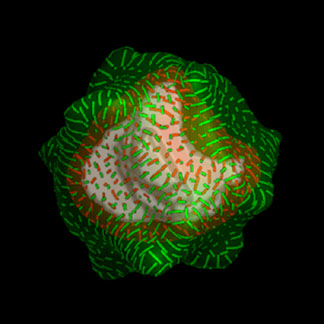
Figure 14: An illustration of the texture interference effects that arise when multiple overlapping transparent surfaces are rendered with principal direction texture strokes.

9    EXPERIMENTAL EVALUATION

Although we have provided theoretical motivation and empirical evidence for the idea that a sparse, opaque texture of principal direction strokes can be used to more effectively convey the presence and shape of a single overlaid transparent surface, as well as its relative depth distance from underlying opaque objects, the actual practical merits of this approach are best objectively determined through controlled observer experiments that quantitatively measure the performance advantages that such textures can offer. In this section, we describe the design and implementation of such an experiment, and discuss the implications of the experimental results.

9.1    Motivation

One might think that it should be possible to judge the relative merits of a proposed visualization paradigm by preparing a few images and making a subjective determination about how effectively the desired information appears to be conveyed. Similarly, it might seem that a side-by-side visual comparison of images generated by each of two alternative data display methods would be sufficient to answer the question of which of these methods it would be preferable to use for a particular application. Designers of visualization techniques make these kinds of subjective decisions all the time while developing new methods for conveying information through images; our "best judgement" is often the major factor determining which avenues of investigation are pursued as promising and which are quickly dropped. But, what if two people looking at the same pictures disagree about their potential usefulness? How can one determine which, if either, of these two subjective opinions is the "correct" one? Furthermore, to what degree does a popular vote of confidence in a display method guarantee its utility? Even if everyone who sees a set of pictures likes them, how do you reliably estimate the extent to which the use of these "better" images will enable improved task performance?

Studies such as the one by Nielsen and Levy [39] do indicate a general positive correlation between subjective preferences for a system and objective performance measures, however this association is by no means guaranteed. Nielsen and Levy cite enough counter-examples to raise serious concerns about the validity of making presumptions about the extent of any potential performance benefits based solely on the results of preference studies, no matter how objective or well-controlled they are. Not only has it been shown in some cases that a technique which appears, for many theoretically well-founded and subjectively evident reasons, to better represent some particular data can repeatedly fail in practice to enable improved performance [28], but the reverse can also be true [27].

Controlled observer experiments can provide a quantitative measure of the practical utility of a visualization paradigm. Carefully designed, they can be used to determine more reliably not only which of two alternative display methods might offer greater practical benefits, but also to estimate quantitatively the relative amount of improvement in performance that might be expected from the better method. However, observer experiments are time-consuming to prepare and execute, and it can be difficult (and potentially costly) to recruit suitably skilled and motivated subjects. Clearly they aren't warranted in all situations.

9.2    Our experimental objectives

The observer study that we conducted was designed to help answer two fundamental questions:

1) does adding artistically-inspired sparse opaque texture to a layered transparent surface really improve the perceptibility of its shape and depth distance from underlying objects, or can this information be as easily and accurately perceived in images in which the transparent surfaces lack this artificial enhancement?

2) does a principal direction texture convey shape and depth information any more accurately or efficiently than simpler existing methods for adding opacity to selected regions of a transparent surface?

9.3    The experimental design

In order that the results of the experiment be as directly relevant as possible to the needs of our driving application, we made two crucial initial design choices: to conduct the experiment entirely with data obtained from actual clinical studies, and to choose a task that was directly implicated in actual treatment plan evaluation. The key objective in radiation therapy treatment planning is to define a distribution of radiation dose that is high enough in the target area to destroy cancerous cells but low enough elsewhere to minimize damage to uninvolved tissues. The main purpose of graphically displaying radiotherapy planning data is to allow the oncologist to obtain a clearer intuitive understanding of the three-dimensional distribution of the dose over the patient anatomy so that he can more easily and effectively weigh the many complex trade-offs that are involved in determining the suitability of a particular treatment plan. The experimental task that we defined was therefore designed to reveal the accuracy with which observers could make judgements that reflected an integrated understanding of the shapes and positions of both an outer transparent surface and an inner opaque object under different texturing conditions.

9.3.1    The experimental task

As the basic experimental task, observers were shown a sequence of images of external transparent isodose surfaces, completely enclosing an opaque inner treatment region, and were asked in each case to specify the point on the outer surface where they felt that it most closely approached the inner. Because of the nature of the test data, in which dose and anatomy surfaces came from treatment plans for actual patients, it was neither realistic to assume the existence of a unique closest point nor practical to construct such examples. We therefore advised subjects that they would be permitted to indicate up to a maximum of three separate points if they felt that the outer and inner surfaces came "equally close" in more than one region.

9.3.2    The experimental setup

Test images were displayed in stereo on a Silicon Graphics Indy with a 70Hz, 1278×1022 resolution, 24-bit color monitor and viewed through a set of Crystal Eyes field- sequential stereo glasses, which effectively halved the vertical resolution to 511. The test images were rendered using a perspective projection, and the stereo and perspective calculations were calibrated for a single pre-defined viewing position 24' from the screen, to which observers were constrained by means of a head rest. We assumed a fixed inter- ocular distance of 64mm for all subjects. For logistical reasons, the experiments had to be conducted on a workstation in a public graphics laboratory that was used by a fairly large number of students on a consistent basis. Temporary curtains were hung to isolate the immediate area surrounding the workstation for the duration of the experiments, and subjects were required to wear earmuffs to minimize any potentially distracting effects from ambient noise. Extraneous illumination was kept as low as reasonably possible under the circumstances, and light levels were measured both at the screen and at the viewing position prior to each experimental run to ensure their consistency between observers. Five highly motivated test subjects agreed to participate in the experiment as a favor to the first author. Three were professional graphic designers, two of whom used computers regularly in their work, and the others were skilled professionals employed in fields unrelated to computer graphics or visualization. Each of the observers was prescreened for stereo ability and adequate visual acuity. Four of the five subjects had a corrected visual acuity of 20/20; subject TCG had uncorrected visual acuity of 20/50. A written set of instructions explained each step of the experimental task, and subjects were generally aware that the objective of the experiment was to measure the effect of surface texture on the perceptibility of shape and depth information.

9.3.3    Task specifics

Each of the trial datasets was pre-rendered at nine successive 2-degree rotational increments, spanning a total of 16 degrees, and observers had the option of either viewing the data as an automatically rocking cine sequence or selecting individual frames of the rotation to view statically. In static viewing mode, observers were provided with a virtual slider that they could use to interactively control the rotational position of the object; in rocking mode, observers could control the speed of the apparent motion by clicking in the viewing window to increase or decrease the time delay between the display of successive frames. Data were always presented in rocking mode at the beginning of each trial, so that we could be sure that observers were exposed to the full range of available shape information in every instance.

Figure 15 shows the view to the right eye of the screen in this first phase of the experiment. The window on the left provides a stereo view of the test dataset, and it is in this window that the object can be viewed in motion or in different iteratively selected orientations. Stereo viewing is disabled in the window on the right, in which observers were asked to specify the locations of the points on the outer surface where it appeared to approach the inner most closely. We felt that it was important to avoid allowing observers to manipulate a probe in depth, because such interactions would have provided an extraneous source of depth information and confused our evaluation of the effect of texture type. Visual feedback was provided during the point specification phase via a 3x3 square of black pixels surrounded by a 1-pixel wide perimeter of white that permitted good visibility over a wide variety of potential background intensities. Observers were advised to be as exact as possible in making their selection, and were allowed to deselect any previously-chosen point by clicking on it.

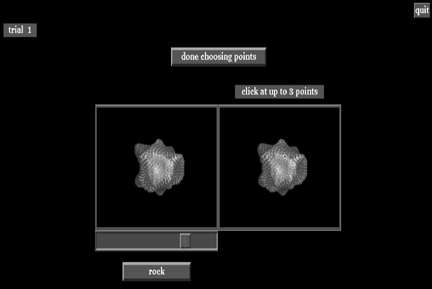
Figure 15: The view to the right eye of the display screen at the beginning of the first trial.

A total of 36 different surface configurations were presented during the experiment, which was organized as a series of 18 separate trials. In one-third of these cases the outer surface was rendered without any texture (plain), in another third the outer surface was textured with grid lines using the solid texturing methods proposed by [29], and in the final twelve instances a principal direction (pdir) texture was used. Figure 16 shows central views of a representative sample of these test stimuli.

Figure 16: A representative sample of the test stimuli used in the experiment.

A single volume texture was used to define the grid lines on all of the surfaces rendered in this particular style, and a consistent uniform spacing was used for the pdir texture in each of the cases where it was applied. We took great care to select the grid spacing and texture element distribution parameters so that surface coverage, measured in terms of the percentage of visible surface points rendered with additional opacity, would be as nearly equivalent as possible in each of the images in which opaque texture was used.

The presentation order of the images was randomly determined and independently defined for each subject. The experiment was self-paced, and observers were allowed to spend as much or as little time on any portion of it as they felt necessary. Two rest breaks were strictly enforced, after the 6th and 12th trials. The number of the current trial was displayed in the upper left-hand corner of the screen at all times, so that subjects could pace themselves and know when to take a break.

In addition to the task of point selection, observers were asked, in a second phase of each two-element trial, to specify in which of the two immediately previous datasets the outer-to-inner distance at the preselected closest points was smallest. Each dataset was initially displayed in a static, two-dimensional image, with the observer's previously selected closest points highlighted by the small black square used in the point selection task. Subjects also had the option of viewing each dataset in automatically rocking, stereo mode, but the locations of the closest points were not shown when the surfaces were displayed in this way. Figure 17 shows a view of the screen during this phase of the experiment.

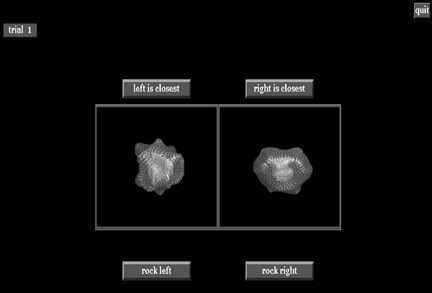
Figure 17: The second experimental task: determining in which of the two displayed datasets the outer surface comes closer to the inner.

Before beginning the experiment, subjects were required to complete a brief training session. This training session consisted of four trials, with two datasets per trial, and was conducted in exactly the same way as the experiment except that after each trial an answer image of the kind shown in figure 18 was displayed, so that subjects could check their work and interpret the differences, if any, between their responses and the "ideal answer". There was no overlap between the surface configurations used during training and during the actual experiment. The outer surfaces were rendered opaquely in the answer images, according to a red-orange-yellow-white colorscale, replicated at the bottom of each image for reference, that varied in a subjectively linear manner according to the magnitude of the shortest outer-to-inner distance at each point. The datasets in the answer images were displayed in stereo, and the points that the observer had indicated as closest were highlighted in black, while the actual closest points were highlighted in white. Subjects could return to viewing the original data by pressing an appropriately labeled button under each window.

Figure 18: An example of the "answer" images shown during the training session.

9.3.4 Data Preparation

The 36 distinct dose/target surface combinations used in this experiment were generated from two registered dose/target/anatomy datasets provided by researchers from UNC Hospitals. After identifying a set of three reasonably-valued but dissimilarly-shaped isolevel surfaces in each dose volume, we scaled the two dose volumes and the two target volumes to approximately equalize the areas that would be enclosed by both the inner and the outer surfaces across the different trials. The volumes containing the external and internal surfaces were then randomly reoriented with respect to each other and to the viewpoint to generate a unique configuration of outer-to-inner distances and reduce the likelihood of learning effects.

9.4 Results and Evaluation

Response accuracy in the first part of each trial was measured in terms of the "geometric miss" of the point selections recorded by each subject -- the distance, in the image plane, between the point or points selected by the observer and the ideal answers, which we defined as any point on the outer surface where the shortest distance to the inner surface was within two voxel units of the minimum, computed over all of the points visible in the central view of that dataset. Figure 19 charts the response accuracy of each subject by graphing the percentage of the total number of selected points, for each texture type, that were located within each of 17 successive distance thresholds of an ideal answer. Figure 20 illustrates the relative extents of several of these different distance intervals. Beyond a certain point, the relevance of this distance metric tends to break down. We chose to stop at a distance representing approximately 10% of the total image diameter. While there are a number of subtle difference between the individual curves, one trend is fairly clear: across all subjects and at nearly all of the offset thresholds beyond 0.5mm, point localization was consistently less accurate in the case of the untextured surface than in either of the cases where opaque surface texturing was applied. The data does not, however, support any assertions about the relative benefits of using one texture type over another. The remainder of the experimental results are not particularly illuminating and will not be discussed further here; a detailed summary of the complete results is available in [22].

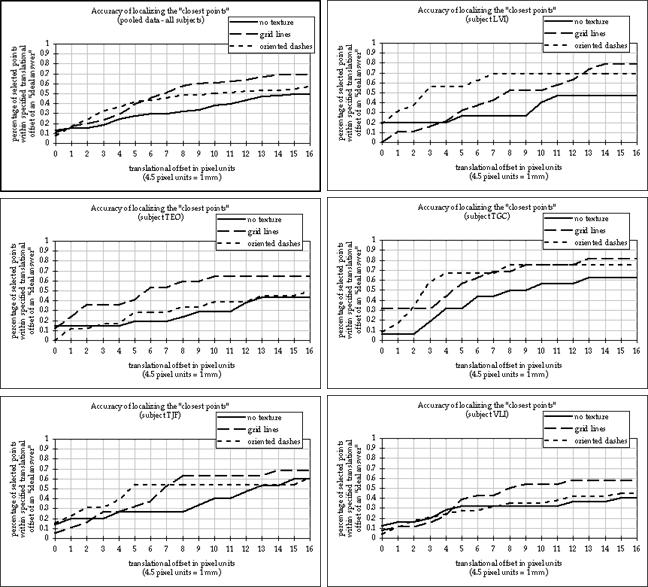
Figure 19: A series of charts depicting the accuracy with which observers were able to localize the closest points between two layered surfaces under different texturing conditions.

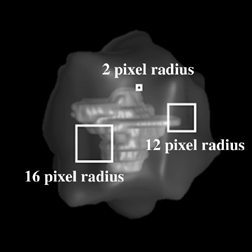
Figure 20: An illustration of the relative extents of several different distance intervals.

Based on the data shown in figure 19, a 3 (type of texture) x 17 (distance interval) repeated measures ANOVA was conducted. Pooling the data from all subjects, significant main effects were found for texture type, F(2,8) = 6.30, p < 0.025, and for distance interval, F(16,64) = 97.61, p < 0.01. A significant interaction between texture type and distance interval was also found, F(32,128) = 4.79, p < 0.01.

A Tukey HSD post hoc comparisons test revealed that the mean percentage of correct point choices, averaged over all 17 distance intervals, was significantly better (p < 0.05) in the case of the grid texture than in the case of no texture. Averaged over all 17 distance intervals, the difference in the mean percentage of correct point choices in the case of the principal direction texture was better, but not significantly better, than in the case of no texture (p < 0.1). The difference in the cases of the principal direction and solid grid textures was negligible.

The Tukey HSD test for the interaction between texture type and distance interval indicated that performance was significantly improved by the addition of a principal direction texture (as opposed to no texture) only for distance intervals of 2-12, and that performance was significantly improved by the addition of a grid texture (as opposed to no texture) only for distance intervals over 5. There were no significant differences between performance under any of the three texture conditions at distance intervals of 0-1. In addition, the comparison between the principal direction and grid displays revealed no significant differences across the broad midrange of intervals (5-11). The principal direction texture appeared to offer more advantage than the grid texture at the smaller distance intervals (1-6), but by a statistically significant amount only at distance intervals of 3 and 4, and the grid texture appeared to offer more advantage than the principal direction texture at the larger distance intervals (7+), but by a statistically significant amount only at distance intervals of 12 and over. Because of the clear inter-observer differences in the patterns of performance under the different texturing conditions, we feel that follow-up studies with a larger number of subjects would be needed before anything conclusive can be inferred about the nature of any performance differences between the two texture types.

There are several possible explanations for the lack of any consistent differences in observer performance in the cases of principal direction and solid grid texturing, despite the very obvious visual differences in the appearances of the two methods. One possibility is that the two textures convey surface shape equivalently well; the other possibility is that between-method differences in the ease of surface shape perception were not well captured by the metrics that we used in this experiment. Several of the subjects indicated after the experiment that while the texture of oriented dashes seemed to provide a more immediate and intuitive impression of surface shape, they felt able, after some additional effort, to deduce an equivalently accurate understanding of surface shape from the grid line images. It would be interesting to test the efficiency as well as the accuracy of surface shape and depth perception, perhaps by repeating this experiment with a new set of observers and comparing the time they spend on the point localization task under each of the texturing conditions. It might also be illuminating to explore additional metrics for evaluating the accuracy with which subjects can correctly identify the point or points of nearest approach between the two overlapping surfaces, to better handle the small but possibly significant number of points that fell "off the chart" because subjects seemed to be aiming at an alternative region of less close approach.

10 CONCLUSIONS

Transparency can be a useful device, in scientific visualization, for simultaneously depicting multiple layers of information. In computer-generated images, as in real life, however, transparent surfaces can be difficult to clearly see and also see through at the same time. By adding opaque texture elements to a layered transparent surface we may enable its three-dimensional shape and relative depth to be more easily and accurately perceived, and a texture pattern that explicitly conveys perceptually relevant characteristics of surface shape may be especially effective.

Line orientation has long been regarded by artists and illustrators as being of significant importance in conveying the shape of objects in two-dimensional drawings, and lines that "follow the form" are believed to portray an object's shape particularly well. We have suggested a method for texturing transparent surfaces with a set of uniformly distributed opaque short strokes, locally oriented in the direction of greatest normal curvature and of length proportional to the magnitude of the curvature in the stroke direction, and have provided an opportunity for empirical comparisons between this surface texturing approach and alternative existing methods.

To quantitatively evaluate the practical merits of this visualization approach, we proposed a novel experimental paradigm for objectively measuring the accuracy with which observers can make integrated judgements about the shapes of two layered surfaces and the depth distance between them. Through a controlled experiment with five subjects, we found significant evidence that shape of an external transparent surface and its relative depth distance from an underlying opaque object could be more accurately perceived when the surface was rendered with a sparse, opaque texture than when it was left plain. We did not find consistent differences in the aggregate accuracy of these judgements, over the entire range of distance intervals, as a function of texture type. Task performance efficiency was not considered in this experiment.

Acknowledgments

The work described in this paper was supported by NIH grant # PO1 CA47982, and was performed as a part of the dissertation research of the first author, who received valuable advice in this effort from Frederick Brooks, Christina Burbeck, Julian Rosenman and Mary C. Whitton. We are very grateful to Dr. Ron Nowaczyk for assisting us in performing the statistical analysis of the experimental results. Marc Levoy provided the volume rendering platform within which we implemented the isosurface extraction and surface texturing functions, and Jim Chung provided the implementation of the marching cubes algorithm that we adapted for the surface triangulation. The radiation therapy data was provided by Dr. Julian Rosenman, UNC Hospitals. The writing of this paper was supported by the National Aeronautics and Space Administration under NASA contract number NAS1-19480 while the first author was in residence at ICASE.

References

[1] Bernhard Bauer-Kirpes, Wolfgang Schlegel, Robert Boesecke and Walter J. Lorenz. "Display of Organs and Isodoses as Shaded 3-D Objects for 3-D Therapy Planning", International Journal of Radiation Oncology, Biology, Physics, 13: 135-140, 1987.

[2] Andrew Blake, Heinrich H. Bülthoff and David Sheinberg. "Shape from Texture: Ideal Observers and Human Psychophysics", Vision Research, 33(12): 1723-1737, 1993.

[3] Jacob Beck and Richard Ivry. "On the Role of Figural Organization in Perceptual Transparency", Perception and Psychophysics, 44(6): 585-594, 1988.

[4] Andrew Blake and Heinrich Bülthoff. "Shape from Specularities: computation and psychophysics", Philosophical Transactions of the Royal Society of London, B, 331: 237-252, 1991.

[5] Michael Brady, Jean Ponce, Alan Yuille and Haruo Asada. "Describing Surfaces", Proceedings of the Second International Symposium on Robotics Research, H. Hanafusa and H. Inoue, eds., pp. 5-16, 1985.

[6] Nicola Bruno and James E. Cutting. "Minimodularity and the Perception of Layout", Journal of Experimental Psychology: General, 117(2): 161-170, 1988.

[7] Patrick Cavanagh and Yvan G. Leclerc. "Shape from Shadows", Journal of Experimental Psychology: Human Perception and Performance, 15(1): 3-27, 1989.

[8] Michael L. Connolly. "Solvent-Accessible Surfaces of Proteins and Nucleic Acids", Science, 221(4612):709-713, 1983.

[9] Bruce G. Cumming, Elizabeth B. Johnston and Andrew J. Parker. "Effects of Different Texture Cues on Curved Surfaces Viewed Stereoscopically", Vision Research, 33(5/6): 827-838, 1993.

[10] James E. Cutting and Robert T. Millard. "Three Gradients and the Perception of Flat and Curved Surfaces", Journal of Experimental Psychology: General, 113(2): 198-216, 1984.

[11] Debra Dooley and Michael F. Cohen. "Automatic Illustration of 3D Geometric Models: Surfaces", Visualization '90, pp. 307-313.

[12] Howard R. Flock and Anthony Moscatelli. "Variables of Surface Texture and Accuracy of Space Perceptions", Perceptual and Motor Skills, 19: 327-334, 1964.

[13] W. Frobin and E. Hierholzer. "Analysis of Human Back Shape Using Surface Curvatures", Journal of Biomechanics, 15(5): 379-390, 1982.

[14] Mami Fukuda and Sergio Masin. "Test of Balanced Transparency", Perception, 23(1): 37-43, 1994.

[15] James J. Gibson. "The Perception of Visual Surfaces", American Journal of Psychology, 63: 367-384, 1950.

[16] Andrew Glassner. An Introduction to Ray Tracing, Academic Press, 1989.

[17] Nikola Guid, Crtomir Oblonsek and Borut Zalik. "Surface Interrogation Methods", Computers & Graphics, 19(4): 557-574, 1995.

[18] Arthur Guptill. Rendering in Pen and Ink, Watson-Guptill Publications, 1976.

[19] Hans Hagen, Stefanie Hahmann, Thomas Schreibner, Yasuo Nakajima, Bukard Wordenweber and Petra Hollemann-Grundestedt. "Surface Interrogation Algorithms", IEEE Computer Graphics and Applications, 12(5): 53-60, September 1992.

[20] David Hilbert and S. Cohn-Vossen. Geometry and the Imagination, translated by P. Nemenyi, Chelsea Pub. Co., 1952.

[21] Elaine R. S. Hodges. The Guild Handbook of Scientific Illustration, Van Nostrand Reinhold, 1989.

[22] Victoria Interrante. Illustrating Transparency: communicating the 3D shape of layered transparent surfaces via texture, Ph.D. thesis, University of North Carolina at Chapel Hill, 1996.

[23] Victoria Interrante, Henry Fuchs and Stephen Pizer. "Enhancing Transparent Skin Surfaces with Ridge and Valley Lines", Visualization '95, pp. 52-59.

[24] Jan J. Koenderink and Andrea J. van Doorn. "Photometric Invariants Related to Solid Shape", Optica Acta, 27(7): 981-996, 1980.

[25] Jan Koenderink. Solid Shape, MIT Press, 1990.

[26] Jan Koenderink and Andrea J. van Doorn. "Relief: pictorial and otherwise", Image and Vision Computing, 13(5): 321-334, June 1995.

[27] Harold L. Kundel. "Perception and Representation of Medical Images", SPIE vol. 1898, Image Processing, pp. 2-12, 1993.

[28] Haim Levkowitz and Gabor T. Herman. "Color Scales for Image Data", IEEE Computer Graphics and Applications, 12(1): 72-80, January 1992.

[29] Marc Levoy, Henry Fuchs, Stephen Pizer, Julian Rosenman, Edward L. Chaney, George W. Sherouse, Victoria Interrante and Jeffrey Kiel. "Volume Rendering in Radiation Treatment Planning", First Conference on Visualization in Biomedical Computing, 1990, pp. 4-10.

[30] Marc Levoy. "Display of Surfaces from Volume Data", IEEE Computer Graphics and Applications, 8(3): 29-37, May 1988.

[31] Margaret S. Livingstone and David H. Hubel. "Psychophysical Evidence for Separate Channels for the Perception of Form, Color, Movement and Depth", The Journal of Neuroscience, 7(11): 3416-3468, 1987.

[32] William E. Loechel. Medical Illustration; a guide for the doctor-author and exhibitor, Charles C. Thomas, 1964.

[33] William Lorensen and Harvey Cline. "Marching Cubes: A High Resolution 3D Surface Reconstruction Algorithm", Computer Graphics (proc. SIGGRAPH 87), 21(4): 163-169, 1987.

[34] Takahashi Maekawa and Nicholas M. Patrikalakis. "Interrogation of Differential Geometry Properties for Design and Manufacture", the Visual Computer, 10(4): 216-237, 1994.

[35] Fabio Metelli. "The Perception of Transparency", Scientific American, 230: 47-54, 1974.

[36] Olivier Monga, Serge Benayoun and Olivier D. Faugeras. "From Partial Derivatives of 3D Density Images to Ridge Lines", Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1992, pp. 354-359.

[37] Henry P. Moreton. "Simplified Curve and Surface Interrogation via Mathematical Packages and Graphics Libraries and Hardware", Computer-Aided Design, 27(7): 523-543, 1995.

[38] Ken Nakayama, Shinsuke Shimojo and Vilayanur S. Ramachandran. "Transparency: relation to depth, subjective contours, luminance and neon color spreading", Perception, 19: 497-513, 1990.

[39] Jacob Nielsen and Jonathan Levy. "Measuring Usability: Preference vs. Performance", Communications of the ACM, 37(4): 66-75, April 1994.

[40] Darwyn R. Peachey. "Solid Texturing of Complex Surfaces", Computer Graphics (proc. SIGGRAPH 85), 19(3): 279-286, 1985.

[41] Photon Treatment Planning Collaborative Working Group. "Three-Dimensional Display in Planning Radiation Therapy: A Clinical Perspective", Int. J. Radiat. Oncology, Biol. Phys., 21: 79-89, 1991.

[42] Henry C. Pitz. Ink Drawing Techniques, Watson-Guptill Publications, 1957.

[43] Penny Rheingans. "Opacity-modulating Triangular Textures for Irregular Surfaces", proc. Visualization '96, pp. 219-225.

[44] Whitman Richards, Jan Koenderink and Donald Hoffman. "Inferring Three-Dimensional Shapes from Two-Dimensional Silhouettes", Journal of the Optical Society of America, A, Optics and Imaging Science, 4: 1168-1175, July 1987.

[45] Takafumi Saito. "Real-time Previewing for Volume Visualization", 1994 Symposium on Volume Visualization, pp. 99-106.

[46] Takafumi Saito and Tokiichiro Takahashi. "Comprehensible Rendering of 3-D Shapes", Computer Graphics (proc. SIGGRAPH 90), 24(4): 197-206.

[47] Michael P. Salisbury, Sean E. Anderson, Ronen Barzel and David H. Salesin. "Interactive Pen-and-Ink Illustration", Computer Graphics (proc. SIGGRAPH 94), pp. 101-108.

[48] Michael P. Salisbury, Corin Anderson, Dani Lischinski and David H. Salesin. "Scale-Dependent Reproduction of Pen-and-Ink Illustrations", Computer Graphics (proc. SIGGRAPH 96), pp. 461-468.

[49] Peter T. Sander and Steven W. Zucker. "Tracing Surfaces for Surfacing Traces", Proceedings of the First International Conference on Computer Vision, 1987, pp. 241-249.

[50] Dino Schweitzer. "Artificial Texturing: An Aid to Surface Visualization", Computer Graphics (proc. SIGGRAPH 83), 17(3): 23-30.

[51] Kent A. Stevens. "The Visual Interpretation of Surface Contours", Artificial Intelligence, 17: 47-73, 1981.

[52] Kent A. Stevens and Allen Brookes. "Probing Depth in Monocular Images", Biological Cybernetics, 56: 355-366, 1987.

[53] Edmund J. Sullivan. Line; an art study, Chapman & Hall, 1922.

[54] James T. Todd and Ennio Mingolla. "Perception of Surface Curvature and Direction of Illumination from Patterns of Shading", Journal of Experimental Psychology: Human Perception and Performance, 9(4): 583-595, 1983.

[55] James T. Todd and Robin A. Akerstrom. "Perception of Three-Dimensional Form from Patterns of Optical Texture", Journal of Experimental Psychology: Human Perception and Performance, 13(2): 242-255, 1987.

[56] James T. Todd and Francene D. Reichel. "Ordinal Structure in the Visual Perception and Cognition of Smoothly Curved Surfaces", Psychological Review, 96(4): 643-657, 1989.

[57] James T. Todd and Francene D. Reichel. "Visual Perception of Smoothly Curved Surfaces from Double-Projected Contour Patterns", Journal of Experimental Psychology: Human Perception and Performance, 16(3): 665-674, 1990.

[58] Georges Winkenbach and David H. Salesin. "Computer-Generated Pen-and-Ink Illustration", Computer Graphics (proc. SIGGRAPH 94), pp. 91-100.

[59] Georges Winkenbach and David H. Salesin. "Rendering Parametric Surfaces in Pen and Ink", Computer Graphics (proc. SIGGRAPH 96), pp. 469-476.

[60] Mark J. Young, Michael S. Landy and Laurence T. Maloney. "A Perturbation Analysis of Depth Perception from Combinations of Texture and Motion Cues", Vision Research, 33(18): 2685-2696, 1993.

[61] Andrew Zisserman, Peter Giblin and Andrew Blake. "The Information Available to a Moving Observer from Specularities", Image and Vision Computing, 7(1): 38-42, 1989.

1. if the viewpoint lies between a concave surface and the caustic defined by the reflected rays, the specular highlight will behave as in the convex case; if the viewpoint is on the caustic, the specular highlight will not be visible.