Math 5421 Spring 2025
Introduction to Climate Models

Assignment 9
due March 28, 2025

Tipping Points

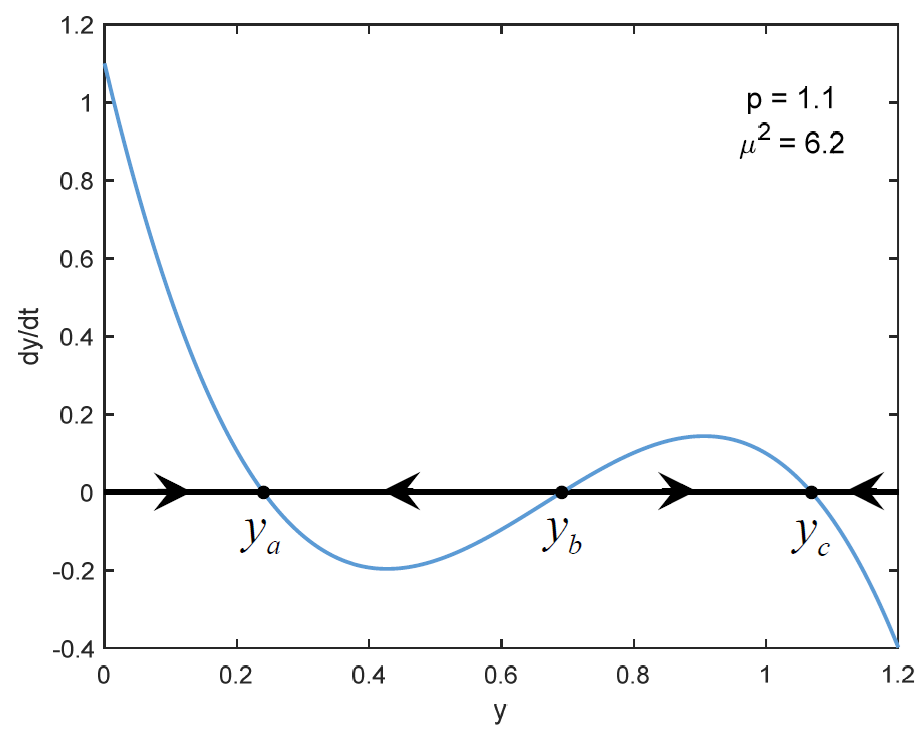Please refer to the slides from the lecture on March 18 discussing Cessi’s model. The equation and one of the figures are repeated here for your convenience. For the exercises, assume that \(\mu^2 = 6.2\). \[ \frac{dy}{dy} = -\left(1 + \mu^2(y - 1)^2\right)y + p \]

Exercise 1

Compute (to four significant figures) the value of \(p_1\) satisfying the properties: \begin{align} 1.1\lt p \lt p_1 &\implies\;\text{ the differential equation has exactly two stable rest points} \\ p_1\lt p &\implies\;\text{ the differential equation has exactly one stable rest point.} \end{align}

Hint: \(p_1\) occurs when the two rest points \(y_a\) and \(y_b\) in the figure have collided to become one rest point.

Exercise 2

Compute (to four significant figures) the value of \(p_2\) satisfying the properties: \begin{align} p_2 \lt p \lt 1.1 &\implies\;\text{ the differential equation has exactly two stable rest points} \\ p \lt p_2 &\implies\;\text{ the differential equation has exactly one stable rest point.} \end{align}

Exercise 3

Suppose the system starts at the equilibrium \(y_a\) when \(p=1.1\). The value of \(p\) is raised to \(1.4\) and left there long enough for \(y\) to become close to the only stable equilibrium. Discuss how to change the value of \(p\) to return the system to a value of \(y\) close to \(y_a\).