Math 5421 Spring 2025
Introduction to Climate Models
Assignment 6 Solutions
 For these exercises, consider Budyko's equation
\[
R\frac{\partial T}{\partial t}
= Qs(y)(1 - \alpha(y,\eta)) - (A + BT) + C(\bar T - T)
\]
with standard parameters \(Q = 343\), \(A = 202\), \(B = 1.90\),
\(C = 3.04\),
\[
\alpha(y,\eta)
= \begin{cases}
\alpha_1 = 0.32, &y\lt\eta, \\
\alpha_2 = 0.62, &y\gt\eta,
\end{cases}
\]
and \(s(y) = 1 - 0.241(3y^2 - 1)\).
For these exercises, consider Budyko's equation
\[
R\frac{\partial T}{\partial t}
= Qs(y)(1 - \alpha(y,\eta)) - (A + BT) + C(\bar T - T)
\]
with standard parameters \(Q = 343\), \(A = 202\), \(B = 1.90\),
\(C = 3.04\),
\[
\alpha(y,\eta)
= \begin{cases}
\alpha_1 = 0.32, &y\lt\eta, \\
\alpha_2 = 0.62, &y\gt\eta,
\end{cases}
\]
and \(s(y) = 1 - 0.241(3y^2 - 1)\).
Exercise 1
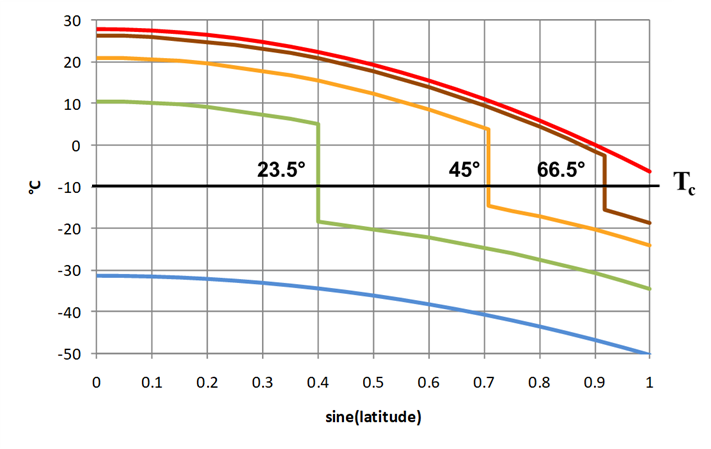
Remove the heat transport in the model by replacing the parameter \(C\) with zero, and consider the ice line \(\eta\) to be a fixed constant. Compute the equilibrium temperature distribution \(T^\star(y)\) and graph the distribution for ice lines at these latitudes: \(23.5^\circ\),\(45^\circ\), and \(66.5^\circ\). Compare the graphs to those of the equilibrium solutions for Budyko's equation with standard parameters. Discuss the differences.
Solution
Setting \(C=0\) in Budyko's equation yields \[ R\frac{\partial T}{\partial t} = Qs(y)(1 - \alpha(y,\eta)) - (A + BT), \] so the equilibrium solution \(T^\star(y)\) satisfies \[ Qs(y)(1 - \alpha(y,\eta)) - (A + BT^\star(y)) = 0. \] Solving for \(T^\star(y)\) yields \[ T^\star(y) = \frac{Qs(y)(1 - \alpha(y,\eta)) - A}{B}. \] Setting \(\eta = \sin{23.5^\circ}\), \(\sin{45^\circ}\), and \(\sin{66.5^\circ}\) yields the following graphs.
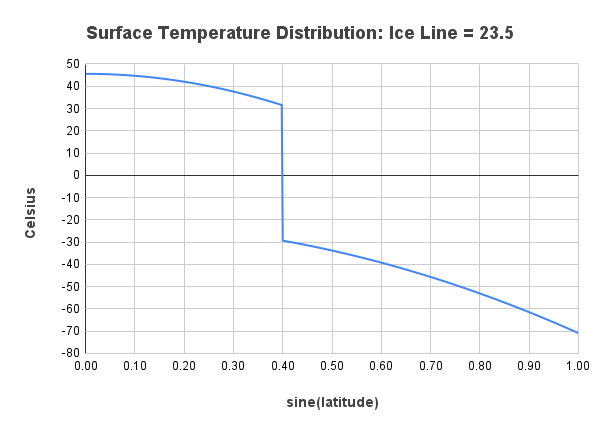
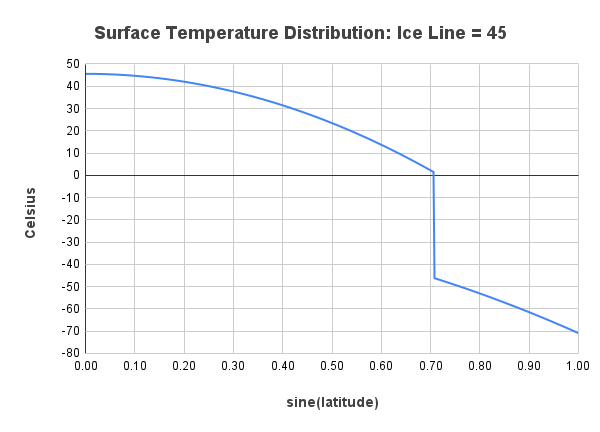
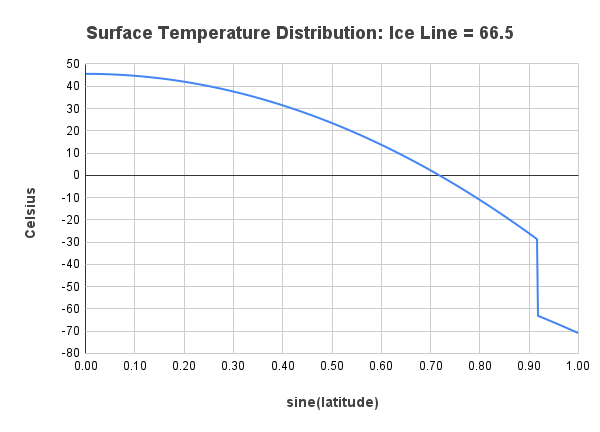
The big difference is that, without the heat transport, the temperature variation across latitudes is much more extreme. For example, with an ice line at 45°, the temperature at the equator with heat transport is about \(21^\circ\text{C}\), while without transport it is about \(45^\circ\text{C}\), or \(24^\circ\text{C}\) warmer. On the other end, with heat transport the temperature at the pole is about \(-24^\circ\text{C}\), while without transport it is about \(-71^\circ\text{C}\), or \(47^\circ\text{C}\) colder.
Another difference is that, without transport, the temperature profile above and below the ice line does not change. The only change is the location of the ice line. The answer in the previous paragraph is the same, independent of the ice line.
Exercise 2
Continuing with Budyko's equation with no heat transport (\(C=0\)), compute the value of \(\eta\) where the ice line condition is met. (The ice line condition is that the average temperature across the discontinuity at the ice line is \(-10^\circ\text{C}\).) Discuss the difference between the location of the ice line in your answer and the locations of where the ice line condition is met for the standard values of Budyko's equation.
Solution
The limit of the equilibrium temperature from the equator as the ice line is approached is \[ T^\star(\eta-) = \frac{Qs(\eta)(1 - \alpha_1) - A}{B}, \] while the limit from the pole is \[ T^\star(\eta+) = \frac{Qs(\eta)(1 - \alpha_2) - A}{B}. \] Therefore, the average temperature at the ice line is \[ \frac12 (T^\star(\eta-) + T^\star(\eta)) = \frac{Qs(\eta)(1 - \alpha_0) - A}{B} = T_c = -10^\circ\text{C}, \] where \(\alpha_0 = \frac12(\alpha_1 + \alpha_2)\). The ice line occurs where \[ s(\eta) = \frac{A + BT_c}{Q(1-\alpha_0)} . \] Putting in the numbers: \[ 1 - 0.241(3\eta^2 - 1) = 0.3241 \\ \boxed{ \eta = 0.569} \]
First of all, there is only one equilibrium ice line location for Budyko's model without heat transport, compared with two locations for the model with heat transport included.
Also, the ice line is at a latitude of 37.4°, which is just South of Memphis, Tennessee. That would put the ice sheet covering most of the United States, which didn't happen during the height of the last ice age.