Examples

Example 8.1: Let , and let satisfy

(1) and ,

(2) , for , and

(3) is strictly increasing on .

The set is an attractor satisfying

Proof: It is a standard exercise to show that is an attractor with . Let

Note that is an attractor block associated with for and that . Therefore, , which establishes the inequality

Now consider the sequence , where , and , for . If , then , which means that . Let satisfy , for , and . Define by

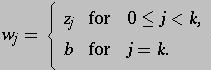
Note that is an -pseudo-orbit for any and that leaves any compact subset of . Since can be chosen arbitrarily close to , this statement implies that

and the proof is complete.

Example 8.4: Let , and let be the general quadratic map in standard form:

There is a unique value of , which happens to be close to , for which there is a superattracting orbit of period with itinerary . In other words, there is a periodic orbit , with , and , for . One can show that

Note that the intensity is of the order when is . Therefore, this particular family of attractors will be extremely difficult to detect by direct computer simulation for even relatively modest periods.

Example 8.5: Let , and let be the time 1 map of the vector field

where are polar coordinates on . For positive values of , this map has two attractors,

where . Note that is an invariant circle, is a set of fixed points, and . Here one can estimate that

for small .

This example appears to be artficial, but it is related to supercritical Hopf bifurcation for maps of the plane. The attractor corresponds to the invariant circle, while the attractor corresponds to the periodic sink with rotation number . One can see that, while the invariant circle is not too difficult to detect with direct computer simulations, even modestly high resonances pose a problem. For example, with 64 bit arithmetic, one can reasonably expect to detect an invariant circle with a radius of . However, one would expect to have difficulty detecting a periodic sink of period 33 for a radius less than . Experience has shown that these resonances are indeed difficult to find with direct computer simulations [1].