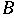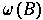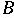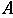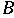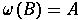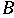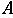If 21.jpg is an attractor block, then 22.jpg is called "the attractor associated with 23.jpg ". If 24.jpg is an attractor and if 25.jpg is an attractor block such that 26.jpg , then 27.jpg is called "an attractor block associated with 28.jpg ". Of course, although the attractor block uniquely determines its associated attractor, many distinct attractor blocks can be found associated with a given attractor.

An attractor block has stronger stability properties than those of the attractor. The attractor itself may change dramatically under perturbation of the system, but the attractor block remains an attractor block under perturbation. This stability is exploited by Conley in his study of the Morse index.

[Left] Attractor blocks
[Up] Main entry point

[TOC] [Glossary] [Help]

Copyright (c) 1998 by Richard McGehee, all rights reserved.
Last modified: July 31, 1998.