MATH 3251, Midterm 2, Fall 1996, Solutions of problems
October 31, 1996.
1(a) The curve is 
.
Its tangent vector 
, which is
at point P. The symmetric equations are
(b) The line y=px has to satisfy the above equations. So, the equation
has to hold for all x. Thus
The last equation means 
, 
, a=1.
Therefore, 
.
2. We have
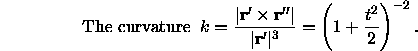
3. The distance from the origin to the plane
is 
. The intersection
of this plane with the sphere
of radius 
is a circle of radius
. Hence the length
. The curvature of a circle is 1/r=1/3
4. We have
At the point 
, we get
and the curvature
Obviously, the minimal value 
for 
.
At the point of maximum, we obtain
hence 
, and
