MATH 3251, Midterm 1, Fall 1996, Solutions of problems
October 17, 1996.
1. We have
,
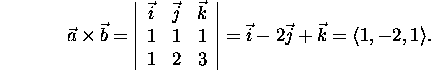
Since 
, and 
are coplanar,
.
2(a). We have
which implies
(b). The area of triangle 
,
(c). The distance from A to the line passing through B and C,
3. A linear equation 
of the plane
passing through the points
, can be found from the property
that, for P(x,y,z) on the plane, the vectors 
, 
, and
are coplanar. This gives
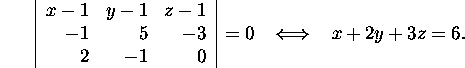
The distance from D to the plane is
4. Since 
,
the vector 
is parallel to both 
and 
,
so we can take 
.
Further, we can take an arbitrary point
, say
, so we obtain
