Exercises
1) Graph the cylinder 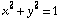 and the hyperbolic paraboloid
and the hyperbolic paraboloid 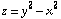 on the same set of axes, and parametrize the curve C where they intersect. Verify Stokes's Theorem for the vector field F(x,y,z)=(
on the same set of axes, and parametrize the curve C where they intersect. Verify Stokes's Theorem for the vector field F(x,y,z)=(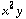 ,
, 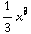 , xy) and the curve C. [i.e. Show that the line integral of F along C equals the appropriate surface integral. You will need to produce your own surface.]
, xy) and the curve C. [i.e. Show that the line integral of F along C equals the appropriate surface integral. You will need to produce your own surface.]
2) Now consider the vector field F(x,y,z)=(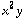 ,
, 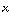 , xy).
, xy).
a) Calculate the line integral of F along the circle parametrized by 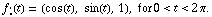
b) Calculate the line integral of F along the circle parametrized by 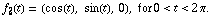
c) Calculate the surface integral of curl(F) over the surface parametrized by g(s,t)=(cos(t),sin(t),s), for 0<t<2 π and 0<s<1.
d) Explain your answers in terms of Stokes's Theorem.
3) Use Stokes's Theorem to evaluate the line integral of the vector field F(x,y,z)=(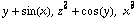 ), where C is the curve parametrized by f(t)=(sin t, cos t, sin(2t)), for 0≤t≤2π.
), where C is the curve parametrized by f(t)=(sin t, cos t, sin(2t)), for 0≤t≤2π.
4) Consider the vector field G(x,y,z)=(x,y,z). Use Stokes's Theorem to prove, by contradiction, that G is not the curl of any smooth vector field F. [Hint: Let M be the unit sphere centered at the origin. The path integral over ∂M of every smooth vector field F equals 0 -- explain why!]
Credits
This lab was written by James Swenson in 2002. In Spring 2004 Jonathan Rogness went through and updated a few minor things to reflect the use of our math2374.nb file.
This lab is copyright 2002 by James Swenson (swenson@math.umn.edu) and is protected by the Creative Commons Attribution-NonCommercial-ShareAlike License. You can find more information on this license at http://creativecommons.org/licenses/by-nc-sa/1.0/.
Although it's not specifically required by the license, I'd appreciate it if you let me know at rogness@math.umn.edu if you use parts of our labs, just so I can keep track of it. Please send me any questions or comments!
Created by
Mathematica
(November 22, 2004)