Homework 10
- Let u(x) be the function that minimizes the integral
among all C2 functions that satisfy the boundary conditions u(0) = 0,u(2) = 0.
- Write out the boundary value problem satisfied by u(x).
- Use the finite element method to approximate the solution. Use an equally spaced mesh with
0 = x0 < x1 <  < xn+1 = 2 < xn+1 = 2 |
|
|
with n = 4, 8, 16.
- By using the poor man’s method to approximate the rms error of your approximations, predict how many mesh points would be required for 6 digit accuracy (assuming no round off error)?
- Find the three finite element functions ωkν(x,y) associated with the triangle with vertices (0, 1), (1,-1) and (-1, 0).
- Write down the elemental stiffnesses for the following triangles: (a) the triangle with vertices (0, 1), (-1, 2), (0,-1); (b) a 30 - 60 - 90 degree right triangle.
- A metal plate is in the shape of an equilateral triangle T with vertices (-1, 0), (1, 0), and (0,
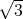 ). The edges of the triangle are fixed at temperature 0 while the center is heated with source f(x,y) = ∥(x,y) - c∥, i.e., the heat source is equal to the distance from center c = (0, 1∕
). The edges of the triangle are fixed at temperature 0 while the center is heated with source f(x,y) = ∥(x,y) - c∥, i.e., the heat source is equal to the distance from center c = (0, 1∕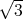 ). The steady state heat distribution u(x,y) of the triangle is given by the boundary value problem
). The steady state heat distribution u(x,y) of the triangle is given by the boundary value problem
| - Δu |
= f(x,y) for (x,y)  T T |
|
|
| u(x,y) |
= 0 for (x,y)  ∂T ∂T |
|
|
- Write down the minimization principle satisfied by u(x,y).
- In order to approximate u(x,y), the plate is divided into smaller equilateral triangles, with n triangles on each side, and the resulting finite element approximation is computed. How many triangles are in the triangulation? How many interior nodes? How many boundary nodes?
- For n = 6, set up and solve the finite element linear system to find an approximation to the temperature of the center of the triangle.
![∫ 2[ ( )2 ] - x du- I[u] = 0 e dx - u dx](hw100x.png)
 < xn+1 = 2
< xn+1 = 2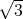 ). The edges of the triangle are fixed at temperature 0 while the center is heated with source f(x,y) = ∥(x,y) - c∥, i.e., the heat source is equal to the distance from center c = (0, 1∕
). The edges of the triangle are fixed at temperature 0 while the center is heated with source f(x,y) = ∥(x,y) - c∥, i.e., the heat source is equal to the distance from center c = (0, 1∕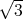 ). The steady state heat distribution u(x,y) of the triangle is given by the boundary value problem
). The steady state heat distribution u(x,y) of the triangle is given by the boundary value problem
 T
T ∂T
∂T