Abstract

One of the well-known challenges in computer vision tasks is the visual diversity of images, which could result in an agreement or disagreement between the learned knowledge and the visual content exhibited by the current observation. In this work, we first define such an agreement in a concepts learning process as congruency. Formally, given a particular task and sufficiently large dataset, the congruency issue occurs in the learning process whereby the task-specific semantics in the training data are highly varying. We propose a Direction Concentration Learning (DCL) method to improve congruency in the learning process, where enhancing congruency influences the convergence path to be less circuitous. The experimental results show that the proposed DCL method generalizes to state-of-the-art models and optimizers, as well as improves the performances of saliency prediction task, continual learning task, and classification task. Moreover, it helps mitigate the catastrophic forgetting problem in the continual learning task.

GD	RMSProp	Adam

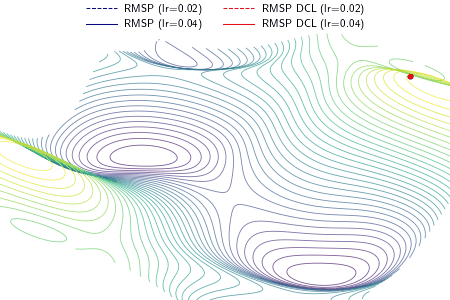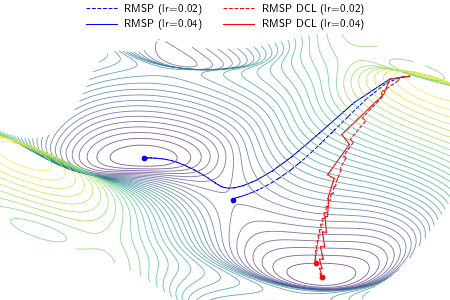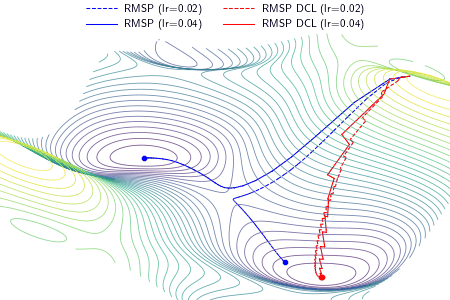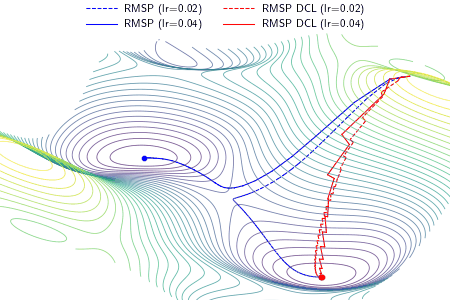
Resources

Paper

Yan Luo, Yongkang Wong, Mohan Kankanhalli and Qi Zhao, "Direction Concentration Learning: Enhancing Congruency in Machine Learning," IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019. [pdf] [bib]

Code

The GitHub repository provides the code for performing our experiments using the proposed DCL method.

Method

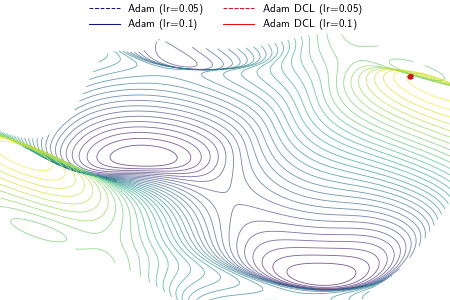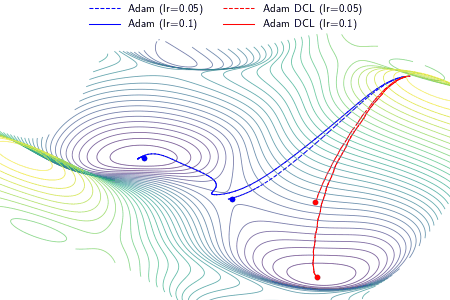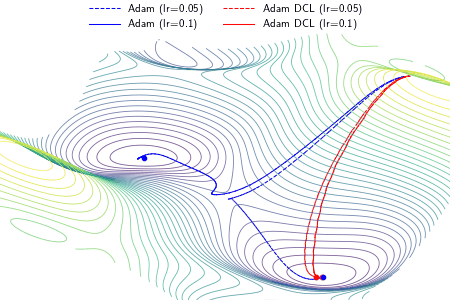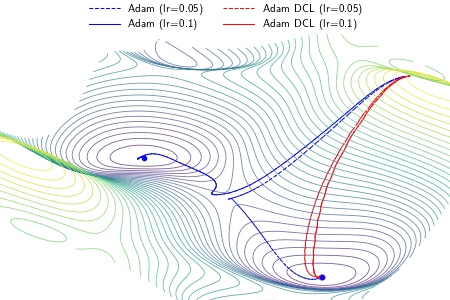
We define congruency to quantify the agreement between new information and the learned knowledge in a learning process, which is useful to understand the model convergence in terms of tractability. We propose a direction concentration learning (DCL) method to enhance congruency so that the disagreement between new information and the learned knowledge can be alleviated. It also generally adapts to various optimizers (e.g., SGD, RMSProp and Adam) and various tasks (e.g., saliency prediction, continual learning and classification).

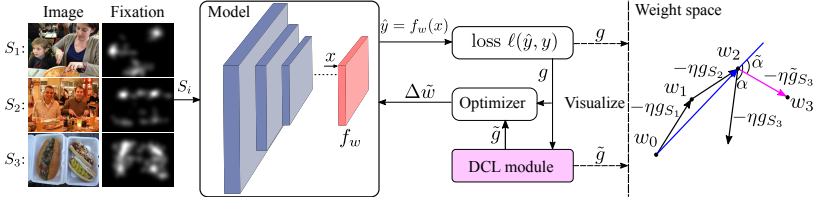
Results

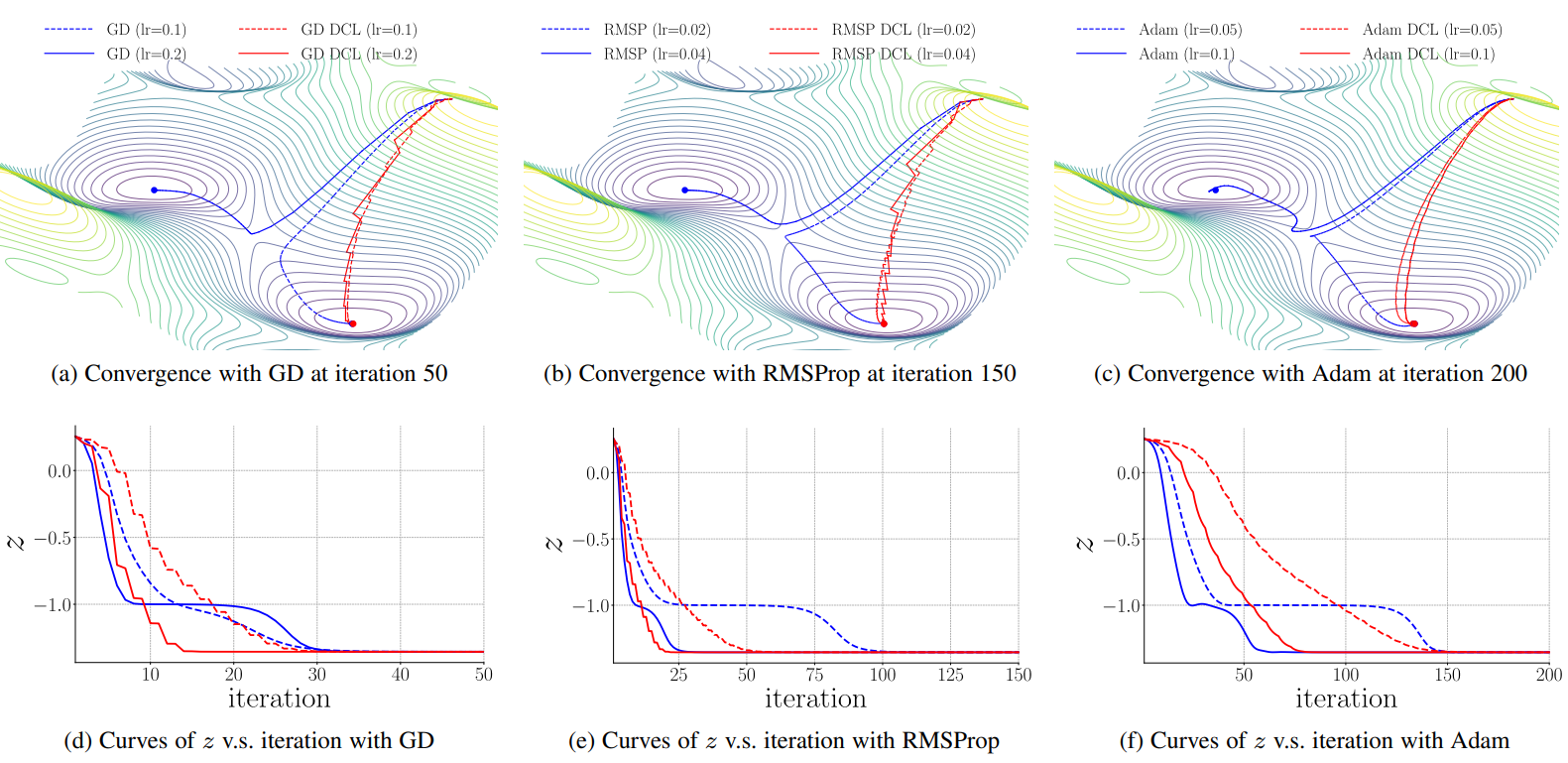
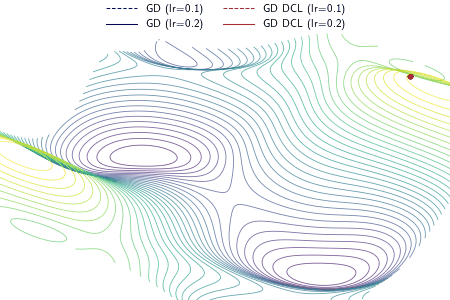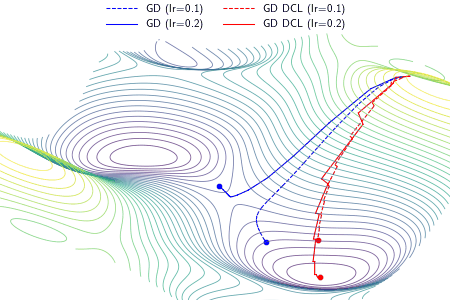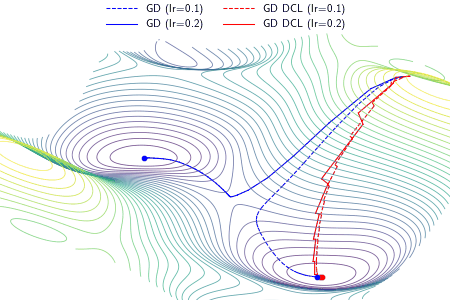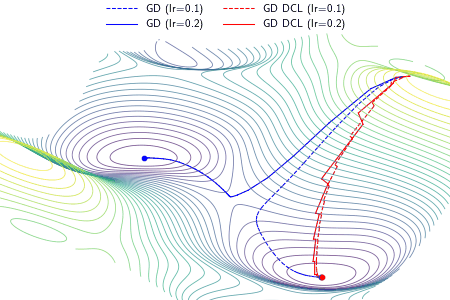
An example demonstrating the effect of the proposed DCL method on three optimizers, i.e., gradient descent (GD), RMSProp, and Adam. In the experiment, except the learning rate, the setting and hyperparameters are the same for ALGO and ALGO DCL, where ALGO={GD, RMSProp, Adam}. The proposed DCL method encourages the convergence paths to be as straight as possible.