Abstract
The Earth Mover's Distance (EMD) is a similarity measure that captures perceptual difference between two distributions. Its computational complexity, however, prevents a direct use in many applications. This work proposes a novel Differential EMD (DEMD) algorithm based on the sensitivity analysis of the simplex method, and offers a speedup at orders of magnitude compared with its brute force counterparts. The DEMD algorithm is discussed and empirically verified in the visual tracking context. The deformations of the distributions for objects at different time instances are accommodated well by the EMD, and the differential algorithm makes the use of EMD in real-time tracking possible. To further reduce the computation, signatures, i.e., variable-size descriptions of distributions, are employed as an object representation. The new algorithm models and estimates local background scenes as well as foreground objects to handle scale changes in a principled way.
Resources
Paper
Qi Zhao, Zhi Yang and Hai Tao, "Differential Earth Mover's Distance with Its Applications to Visual Tracking," in IEEE Transactions on Pattern Analysis and Machine Intelligence (T-PAMI), Volume 32, Issue 2, Pages 274-287, February 2010. [pdf] [bib]
Qi Zhao, Shane Brennan and Hai Tao, "Differential EMD Tracking," in IEEE International Conference on Computer Vision (ICCV Oral Presentation), Rio de Janeiro, Brazil, October 2007. [pdf] [bib]
Overview
The main theoretical contribution of the paper is the derivation of a differential formula to compute the derivative of the EMD with respect to the location so as to locate the object quickly. Since the formulation of the EMD is a linear programming problem, derivative of the EMD can not be directly computed. To overcome this difficulty, we propose a two-phase algorithm, as depicted in Figure 1.
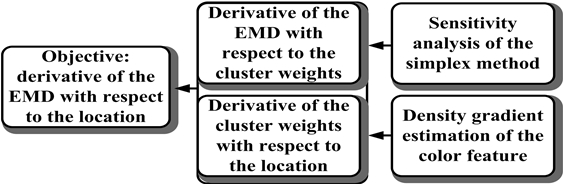
Fig.1 Overview of the DEMD algorithm.
Results
(click the images to play videos)
A. Example of the DEMD Tracking
Fig. 2 Indoor sequence.
Left: using the MS tracker, the MS tracker loses the object quickly as the color of the pedestrain changes due to reflection.
Right: the DEMD tracker manages to track the pedestrian throughout the entire sequence.
Fig. 3 Highway-Car sequence.
Left: the MS tracker starts to wander when the car is entering the strong shadow and fails around frame 13.
Right: the DEMD tracker successfully follows the car into and out of strong shadows.
Fig. 4 Running-Girl sequence.
Left: the MS tracker has lost track of the girl by frame 10, when she is running under the shadow.
Right: the DEMD tracker maintains a secure focus on the object throughout the sequence though there are shadows all along the path and the object is moving fast.
B. Examples of the DEMD Tracking with Background Modeling (DEMDB)
Fig. 5 OTCBVS Sequence
Left: the performance of the DEMD tracker degenerates as the object becomes smaller and eventually loses track of it.
Right: the DEMDB tracker keeps tight track of the object.
C. Quantitative Results
Fig. 6 Tracking results of several public data of the proposed DEMD tracker with background modeling (DEMDB) and its comparison with the standard Mean Shift (MS) Tracker. From left to right are the Red-Coat Female, White Van, Female - Corridor View, Male - Corridor View and RedTeam sequences. First row: results using the MS tracker; second row: tracking results using the DEMD tracker.

Table 1. Quantitative results for public data using the proposed DEMD tracker, DEMD tracker with background modeling (DEMDB) and the MS Tracker. In datasets with *, ground truth was provided every 10 frames and we count only those frames with ground truth for comparison. Others have ground truth for each frame.



















