The normal distribution

The normal distribution curve is given by the function:

The mean = 0, and the standard deviation = 1.

The total area under the curve = 1. So the value A(1) = .3413 in Table 11.3 (on page 204 of the notes) means that about 34% of the area under the normal curve is between the lines x = 0 and x = 1.

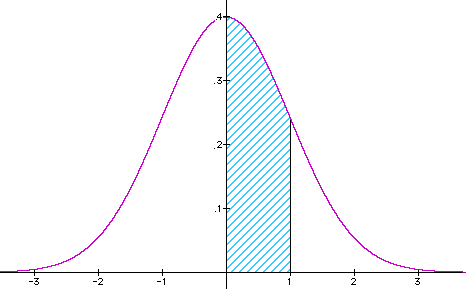
So, by symmetry, the area between the lines x = -1 and x = +1 is 2·0.3413 = 0.6826.

Thus, about 68% of the total area under the normal curve is between these two lines.

We say that a random variable is distributed normally if its distribution looks like the normal curve, after shifting to get the correct mean and re-scaling (stretching or shrinking) to get the right standard deviation. So, it follows from the discussion above that if a random variable is distributed normally, then the probability of a value being within 1 standard deviation of the mean is about 0.68.

Example: Suppose that scores on an exam are normally distributed,
with mean = 80 and standard deviation = 8. Then the scores which are
within 1 standard deviation of the mean are between 80 - 8 = 72 and 80 + 8 = 88.
 
 

Using the Table 11.3 again, the value A(2) = 0.4772 means that about 47.7% of the area under the normal curve is between the lines x = 0 and x = 2.

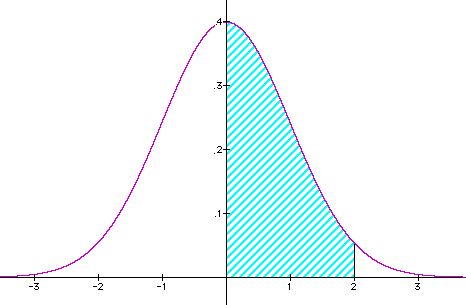
By symmetry, it follows that about 95.4% of the area under the normal curve is between the lines x = -2 and x = 2. So, if a random variable is normally distributed, then the probability of a value being less than 2 standard deviations away from the mean is 0.954.

In our example (with  and) around 95.4% percent of the scores are between 80 - 2·8 = 64 and 80 + 2·8 = 96.