Math
3107, section 2 June
3, 1999
Recommended review problems
Part I: Problems about §11.5
-
Review the group exercises and assigned homework problems
from this section . . .
-
This series of exercises gives additional practice similar
to a series of exercises that we did in class.
An airline is going to book n passengers
for a flight, where n is a (possibly unknown) number. Let p
be the probability that that a given passenger will actually board the
flight.
-
Determine the expected number
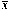 of passengers that actually board the flight:
of passengers that actually board the flight:
(i) if p = .85 (thus 15% no-show),
then 
(ii) if p = .95 (thus 5% no-show),
then 
(Your answer will be an expression that involves
n.)
-
Determine the standard deviation
 in the number of passengers that actually board the flight:
in the number of passengers that actually board the flight:
(i) if p = .85, then 
(ii) if p = .95, then 
(Your answer here also will be an expression that
involves n.)
-
Find the z value (from the table in the notes)
such that 85% of the area under the normal curve is to the left of that
value.
Suggestions: (1) find the value of
A(z)
by solving the equation .5 + A(z) = .85
(2) determine which column of the table
in which to locate this value!!
-
Suppose that the airplane seats 200 passengers. Write
the equation which expresses the condition that the airline can book n
passengers and will not have to "bump" passengers 85% of the time:
(i) if p = .85
(ii) if p = .95
-
Simplify and solve your equations, and determine how
many tickets the airline can sell.
Suggestions: Starting from the same
equation as in Exercise 11.5.9 in the notes, you can get an equation that
involves n and 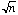 .
You can turn it into a quadratic equation by using the auxiliary unknown
.
You can turn it into a quadratic equation by using the auxiliary unknown 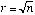 .
(Note that this gives
.
(Note that this gives 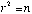 .)
Use the quadratic formula to solve this version of the equation.
.)
Use the quadratic formula to solve this version of the equation.
Part II: Problems about chapter
12
-
Review the group exercises and assigned homework problems
from this chapter . . .
-
Find the multiplicative inverses of the nonzero elements
of F7, the system of integers mod 7.
(In other words, find the solutions of the equations
ax=
1 in F7, for a = 1, 2, 3, 4, 5, 6.)
Here, it may be useful to review section 6.3,
from the chapter on modular arithmetic.
-
This set of exercises refers to the multiplication table
for a field with 4 elements that was constructed in class on Wednesday.
To have a notation for this system, we will call
this field F4. Note, however, that it is not the
system of integers mod 4.
As usual, the system of integers mod 2 will be denoted
F2.
As explained in class, F4 can be considered as an extension
of F2, so that identities such as 1 + 1 = 0 which hold
in F2 will continue to hold in F4,
-
Use your addition and multiplication tables to calculate
the value (in F4) of x2 + x
+ 1 for:
(i) x = 0 (ii) x
= 1 (iii) x = 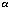 (iv) x =
(iv) x = 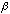
-
What are the roots (in F4) of the
equation x2 + x + 1 = 0?
Suggestion: use the results of part
(a) to answer this.
-
Fill in the following chart with coefficients from F2
(integers mod 2).
[The mathematical point here is that every element
of F4 turns out to be of the form 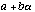 ,
where a and b are elements of F2.]
,
where a and b are elements of F2.]
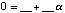
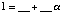
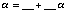
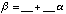
Comment: The entries here will
just be zeros and ones!
-
Verify that
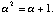
Suggestion: This actually follows from one of the previous
parts of this exercise.
Just remember that -1 = +1 in F2 and therefore also
in F4,
-
Let a, b, c, d be elements of F2. Calculate the
following expression:
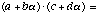
Use the result of d) to simplify the answer (so that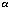 just
appears to the 1st power). Your answer should be of the
following form:
just
appears to the 1st power). Your answer should be of the
following form:

-
Use the multiplication table to calculate:
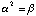
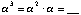
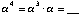
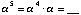
Comment: The entries here should
be elements of F4,
-
Do you see a pattern in the above?
 of passengers that actually board the flight:
of passengers that actually board the flight: in the number of passengers that actually board the flight:
in the number of passengers that actually board the flight: