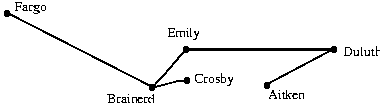
Problem # 1 The figure below shows a tree network on 6 towns. Construct the corresponding list of 4 towns.

Solution:

1. Remove Fargo, add Brainerd to the list.
2. Remove Crosby, add Brainerd to the list. (Brainerd becomes a terminal)
3. Remove Brainerd. add Emily to the list. (Emily becomes a terminal.)
4. Remove Emily, add Duluth to the list.

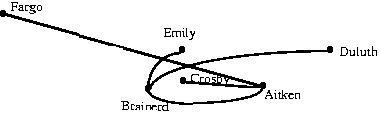
Problem #2 Here is a list of 4 towns: (Aitken, Brainerd, Aitken, Brainerd).
Construct the corresponding tree network on the six towns:
Aitken, Brainerd, Crosby, Duluth, Emily, Fargo.

Solution:

1. Join Fargo to Aitken.
2. Join Emily to Brainerd.
3. Join Duluth to Aitken. (Aitken becomes a "terminal")
4. Join Crosby to Brainerd. (Brainerd becomes a "terminal")
5. Finally, join the 2 remaining "terminals", Aitken and Brainerd.

Problem #3 (a) How many labeled trees are there with 7 vertices?

Solution: By Cayley's formula, there are 7⁵ of them.
 
   (b) How many lists of 5 towns (possibly with repetitions) can be constructed from a given set of 7 towns.
 
   (c) Explain why the answer in part (b) is correct.
For instance, how many choices for each item on the list (?) . . .

Solution: The number is the same as in Cayley's formula: 7⁵.
To check this, note that there are 7 choices for each of 5 places on the list
and thus 7·7·7·7·7 = 7⁵ possible lists.

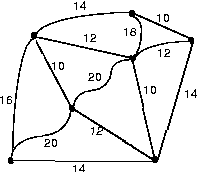
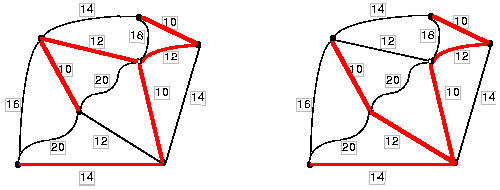
Problem #4    The relative costs of removing snow from the roads between 7 houses are shown below. Determine which roads should be plowed so that every house is reachable from every other house and snowplowing costs are minimized.

Problem #5 There are 6 teams in a certain sports league. We will identify them by the letters A,B,C,D,E,F. In their championship tournament, a team is eliminated when it loses a game.

1. How many games have to be played to determine the championship?

Solution: 5 games are needed, since one team is eliminated in each game.
2. (b) Draw a binary tree that represents a tournament for this league, with no more than 3 rounds. (So, there should be no more than 4 generations in the tree.) Label the leaves of the tree with the letters that identify the teams.

Solution:

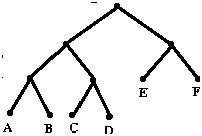
(c) Is it possible to set up such a tournament in more than one way? _______

If you answered "yes", draw the tree that represents a different possible tournament.

If you answered "no", explain why it can be set up in only one way.

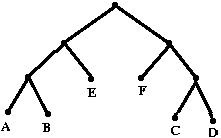
Solution: The correct answer is "yes".
Here is a different tournament that has the required properties:

Back to the class homepage