Math 3118, section 1
Fall 2002
Miscellaneous group problems for Wednesday, October 16

1. Do the following calculations with complex numbers:
    
   1. Let  a, b, c, and d be real numbers. Set  z = a + bi and  w = c + di.
      Calculate
       
      • =
         
      • =
         
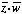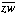        (Calculate the two expressions separately; then verify that they are equal to each other.)
         
         
   2. If  z = a + bi is a complex number, calculate the following:
       
       
   • z² =                                        and     =
      
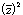     How are the answers related? (An answer of a few words should be possible!)
      
      
   • z³ =                                         and     =
      
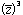     How are the answers related? (An answer of a few words should be possible!)
      
      
   • z^k=                                       and     =
      
     Don't try to work it out algebraically; just try to figure out how the two answers are related!
      
      
      
2. Let  f(x) = x³ + 3x² + 1, and let  z = a + bi be a complex number.
    
   How are the complex numbers  f(z)  and  f() related to each other?
     
   Suggestion: The answers to parts a and b of the previous problem can provide useful information.
    
    
    
3. The graph of  f(x) = x³ + 3x² + 1  is shown below:
    
                          
    
1. Use the graph to determine how many real solutions the equation  f(x) = 0  has.
    
    
2. Suppose that  z = a + bi  is a (non-real) solution of the equation  f(z) = 0.
    
   What is another solution of this equation?