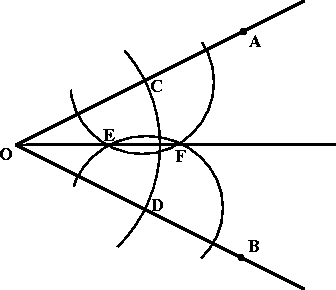

We're given the angle –AOB
Step 1. Draw a circular arc centered at O.
Step 2. Let C and D be the points where the arc intersects the sides of the angle.
Draw (sufficiently large circular arcs centered at C and D respectively. Let E and F be the points where these two arcs intersect. Draw the line joining E and F. (This line should go through the point O.)
Step 3. We claim that the line EF is the bisector of the angle >–AOB.
II. Why does the construction work?

Step 1. CF = DF because the two circles have equal radii. So, DCOF @ DDOF by the SSS property.
Step 2. DACD @ DBCD by the SSS property. (Note that CD is congruent to itself.)
Step 3 (conclusion).
–COF @ –DOF because corresponding parts of congruent triangles are congruent. Equivalently, –AOF @ –BOF. This proves that EF is the bisector of –AOB.
Back to the HW suggestoins.
Back to the class homepage.