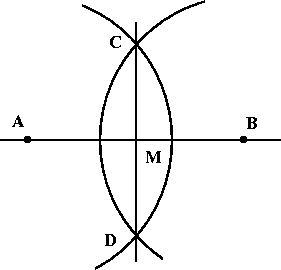
Math 3118, section 3
We're given the segment AB
Step 1. Draw (sufficiently large) circular arcs (of equal radius) centered at A and B respectively.
Step 2. Let C and D be the points where the two arcs intersect.
Draw the line that connects C and D. This line intersects the segment AB at the point M.
Step 3. We claim that (i) M is the midpoint of the segment AB, and (ii) the line CD is the perpendicular bisector of the segment AB.

Step 1. AC = BC because the two circles have equal radii. So, DACB is isosceles, and –ACB @ –ABC
Step 2. DACD @ DBCD by the SSS property. (Note that CD is congruent to itself.)
Since corresponding parts of congruent triangles are congruent, –ACD @ –BCD.
Step 3. DACM @ DBCM by the ASA postulate. (The point of steps 1 and 2 was just for checking the required angles for this step.) Since corresponding parts of congruent triangles are congruent, AM = BM, and –AMC @ –BMC. Since these two angles add to 180º, it follows that they are right angles.
Step 4 (conclusion). Since AM = BM, we conclude that M is the midpoint of AB.
Since –AMC and –BMC are right angles, the lines CD and AB are perpendicular.
Thus, we have constructed the perpendicular bisector.
Back to the HW suggestions.
Back to the class homepage.