Math 3118, section 1
Fall 2002
Review problems for test #2

1.   Let  f(x) = x3 + 3x2 - 3, where x is a real variable.

  1. Fill in the following table of values:

      x

     -4

     -3

     -2

     -1

      0

      1

      2

     
     f(x)
     

      

      

      

      

      

      

      

     
  2. On which of the following intervals does the Intermediate Value Theorem say that f(x) has a real zero?
     
  3.   (Optional)   If you have a graphing calculator, plot the graph of  f.
     

2.   Compute the following complex numbers:

  1. (3 + 4i )·(4 + i)
     
  2. (3 + 2i )·(2 - i)
     
  3. the complex conjugate of 4 + 3i
     
  4. the complex conjugate of - 6i
     

  5.  

  6.  

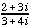
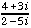
3.  Use the method of exercise 10.2.9 to approximate 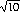.  Start with  a = 3,  and stop when you get
a rational number  c  such that  c2 - 10  is less than  .00000001 = 10-8.
 

4.   Find all of the zeros of the polynomial:

              x3 + 2x2 - x - 2

Factor this polynomial as a product of 3 linear factors.
  

5.   Find a rational zero of each polynomial, and then factor the polynomial as a product of a linear factor and a quadratic factor.

  1. 2x3 - 7x2 + 5x - 1
     
  2. x3 - 7x2 + 5x + 1    
     

6.   For each polynomial in the preceding problem, find all of its zeros (whether rational, real, or complex).
Suggestion: Use the quadratic formula to find the zeros of the quadratic factor.
 

7.

  1. Explain why 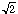  and   are algebraic.
  2. Write  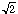( + )2  as  A + B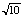, where  A and  B are rational numbers.
  3. Write  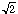( + )4  as  A + B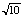, where  A and  B are rational numbers.
  4.  Find a rational number  S   such that ( 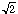+ )4  + S(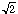 + )2  is a rational number.
    Note: Your answer actually may be an integer.
    Suggestion:   Use the answers from parts b and c;  try to adjust things so that 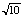  disappears from the expression.
  5.  Find a rational number  T  such that  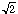( + )4  + S(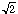 + )2  + T = 0,  where  S   is the number that was found in part d.
    Suggestion:   You may be able to solve this part by making minor modifications to your previous answers and calculations.
Comment: (The answer to 7e shows that 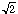 +  is also algebraic.)
 

8.  A few exercises from the text, related in various ways to problems that we have worked on.

  1. = Exercise 10.1.13
     
  2. = Exercise 10.2.1
     
  3. = Exercise 10.4.11
     

9.   Review the exercises that were done as group work and homework assignments
 

   

Solutions are linked here  

   

Back to the class homepage