Math 3118, Section 1
Fall 2002
Partial review of chapter 8:
      Some key concepts from Sections 8.2, 8.3, and 8.4

1. The parametric form of the line through two given points.
   • Let  A = (a,b) and  B = (u,v) be two points in the plane.
     • The direction indicator of the line joining  A and  B is  D = B - A.
     • In terms of the coordinates,  D = (u,v) - (a,b) = (u-a, v-b).
       (See Figure 8.3 in the text.)
         
     • So, if a person starts travelling in a straight line from  A, and covers the distance from  A to  B in 1 unit of time, then the person's position at time  t is given by the formula
                    P(t) = A + tD, or equivalently  P(t) = A + t(B - A).
       We also refer to this formula as the parametric form of the line.
         
     • A line given parametrically with the same starting point  A and direction indicator 
       2D= (2(c-a),2(d-b)),then it is the same line, but the traveler is moving twice as fast.
       (Also see Exercise 8.2.17, a recommended review problem).
         
     • Two lines with the same direction indicator are parallel (or the same …).
       Similarly, a line with direction indicator  kD, where  k is a real number, is parallel to a line with direction indicator  D (unless it is the same line).
        
     • Find the direction indicator and the parametric form of each of the following lines:
       1.   The line joining  (-1,3)  and  (2,1).
       2.   The line through  (1,5)   parallel to the line found in part a.
       3.   The line joining  (a,b)  and  (c,d).
           
       Click here to see the answers.
        
        
2. Vector addition, vector subtraction, and plane geometry.
   (Related to Exercise 8.2.24, a recommended review problem.)
   • Let  A = (a,b) and  B = (c,d) be two points in the plane.
   • Then  A+B = (a+c, b+d). This is shown in the sketch below, for  A= (2-1)  and  B= (3,2).
       
       
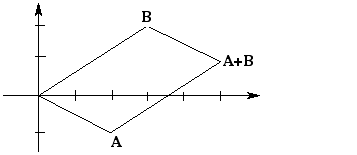
   • What are the direction indicators of the following lines? (Try it for the particular points 
     A= (2-1)  and  B= (3,2) and also in general, i.e., for abstract points  (a,b)  and  (c,d).)   
   1. The line joining  (0,0)  and  A.
   2. The line joining  B and  A + B.
   3. The line joining  (0,0)  and  B.
   4. The line joining  A and  A + B.
       
   • Which of the above pairs of lines are parallel? What kind of quadrilateral
     is formed by the four points  (0,0), A, B, and  A + B?
       
   Click here to see the answers.
    
3. Finding the slope of a line from its parametric form.
   (Also see Exercise 8.2.14 and Exercise 8.2.19, a recommended review problem.)
   • Let a line be given parametrically, with direction indicator  D = (c,d).
   • If the starting point is  A = (a,b), then the position at time  t is:
              P(t) = A + tD.
   • For practice, sketch this with  A= (1,3)  and  D = (2, -1).
     Calculate  P(0)  and  P(1)  in this case.
   • Use the answer from the previous part to calculate the slope of the line.
   • Calculate  P(0)  and  P(1)  for  P(t) = A + tD, where  A = (a,b) and  D = (c,d).
   • Use the answer from the previous part to calculate the slope of the line.
     (Simplify your answer as much as possible.)
        
   Click here to see the answers.
   
    
4. Finding the parametric form of a line from its slope-intercept equation.
   (Also see Exercise 8.2.18)
   • If the equation of a line is given as  y = mx + b, (this is called the  slope-intercept form of the equation) we can represent the line parametrically as follows:
   • Find two points on the line (for instance by substituting two different x-values and then calculating the corresponding y-values).
   • Use the methods of I. above to find the parametric form.
       
   • So, the conclusion from III and IV is that it's possible to go back and forth between the two ways of describing a line.
        
5. Norms and distances
   • Let  P = (x,y) be a vector.
   • By definition, the  norm of  P is .
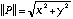   • If we think of P = (x,y) as representing a point of the plane, then the Pythagorean theorem tells us that the norm of  P is the distance from  (0,0)  to  P.
   • If we think of a vector D as being an arrow, then the norm  ||D||   is just its length.
   • So, in general, we need an ordered pair of numbers to specify a vector, but its norm is just a number.
   • If  P = (a,b) and  Q = (c,d) are two points, then  ||Q - P||, the norm of the difference, is the distance from  P to  Q:
   1. Q - P = (c-a, d-b), so that:
   2. 
   • For practice, sketch this with  P= (1,3)  and  Q = (2, -1), and calculate ||Q - P||.
       
   Click here to see the answers.
    
    
6. Segments
   • Let the line joining  A and  B be given in parametric form:
          P(t) = A + t(B - A).
   • P(0) = A,  and  P(1) = B.  Points of the segment AB are points  P(t), where  t ranges
     through the numbers between 0 and 1. So,  t= 0  and  t= 1  give the endpoints, and is the midpoint.
   • Calculate for the following cases:
   1. A= (-3,2)  and  B= (4,0)
   2. For two "abstract" points  A and  B. Simplify so that  A  and  B  each appear just once. (If you're using coordinates, get your answer into a form where each coordinate appears just once.)
   • Calculate for the following cases:
   1. A= (-3,2)  and  B= (4,0)
   2. For two "abstract" points  A and  B. (Simplify your answer, as above).
        
   Click here to see the answers.
    
    
7. The dot product and orthogonality
    
   • Calculating the dot product
     • If  P = (a,b) and  Q = (u,v), then the dot product P·Q is given by the formula:
             P·Q = au + bv.
       Sample: If P = (1,3),  and  Q = (5,-3),  then  P·Q = 1·5 + 3·(-3) = 5 - 9 = -4.
       So, the dot product of two vectors is just a number.
        
     • Calculate  P·Q in the following cases:
       1. P= (2,-1)  and  Q= (4,3)
          Sketch these two points in the plane, and draw their "position vectors",
          i.e., draw an arrow pointing from the origin to each point.
           
       2. P= (2,4)  and  Q= (6,-3).
          Sketch these two points in the plane, and draw their "position vectors",
          i.e., draw an arrow pointing from the origin to each point.
          What can you observe about the angle formed by the line joining  (0,0)  to  P and the line joining  (0,0)  to Q?
           
       3. P= (4,3)  and  Q = P= (4,3).
          Also, calculate  ||P|| and compare this with the dot product  P·P.
           
       4. P= (a,b)  and  Q = P= (a,b).
          Also, calculate  ||P|| and compare this with the dot product  P·P.
           
       Click here to see the answers.
        
   • Norm of a sum
     • The solution of Exercise 8.4.4 says that:
             ||P + Q||² = ||P||² + ||Q||² + 2P·Q.
       Thus, we need to add 2 times the dot product as a "correction term".
        
     • If the line from  (0,0)  to  P is perpendicular to the line from  (0,0)  to  Q, then the parallelogram formed by   (0,0), P, Q, and  P+Q is actually a rectangle. So, th e Pythagorean theorem tells us that  ||P + Q||² = ||P||² + ||Q||² in this case.
       Thus, the correction term must be zero if these two lines are perpendicular. We express this by saying that  P and  Q are orthogonal. In other words:
         P·Q= 0  if and only if  P and  Q are orthogonal.
        
     • Is each pair orthogonal?  (compare with your sketches from above.)
       1. P= (2,-1)  and  Q= (4,3)
       2. P= (2,3)  and  Q= (3,-2).
           
       Click here to see the answers.
        
     
      

   Back to the class homepage