Supplementary exercise #1 Consider the same triangle ABC as in problem 30 of §2.5.
- Sketch the line joining A to the point
(0,1/3,2/3)
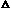 (which lies on the line
(which lies on the line
 ).
).
- Show that for every point
(r,s,t)
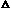 of this line,
the equality of ratios
s/t =
1/2 holds.
of this line,
the equality of ratios
s/t =
1/2 holds.
- Show that, more generally, if P =
(0,b,c)
 is a point of the line
is a point of the line
 , then for every point
(r,s,t)
, then for every point
(r,s,t) of the
line joining A and P, the equality
of ratios
s/t =
b/c holds.
of the
line joining A and P, the equality
of ratios
s/t =
b/c holds.
Hint for §3.12; problem 59 Here's a diagram of the setup:
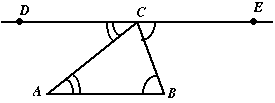
Here's an alternate version of the setup which is quite
acceptable, and actually quite compatible with the general approach of
our text. [I looked this up somewhere; I'll divulge the identity
of my source at some later date . . . ] The idea is to
define E by saying that its coordinate vector is
given as E =C + (B - A)
and similarly to define D by saying that its
coordinate vector is given as
D =C + (A - B). This
guarantees immediately that we have opposite rays [do you see the
reason for this/], and it's also not hard to see that the hypotheses
of the proposition about alternate interior angles are verified.
(This is a small additional price that we have to pay for using this
alternate approach, but it seems much more manageable
than the proof of oppositeness of the rays in the other approach.)
Oh yes, there's one other thing that musn't be neglected,
either under this approach or under the other approach. Namely, we
have to show [for instance] that the ray
Hint for §3.12; problem 68 Let
(r,s,t) Supplementary exercise #2 Given triangle
ABC,
let P be the midpoint of
Supplementary exercise #3 Given triangle ABC
and triangle PQR. Assume that there exists a nonzero
real number v such that: Show that if the orthocenter of triangle ABC
is (r,s,t) Supplementary exercise #4 Let triangle ABC
and triangle PQR be as in Supplementary exercise #2,
and let (r,s,t)
Comments and questions top;
roberts@math.umn.edu
Back to to the homework list.
Back to the class homepage.
![]() is in the interior of the
angle CBD, in order to apply the result about
angle addition. Under our approach it isn't too difficult.
It may require some thinking, but if you go back to the definition of
interior of an angle (and maybe another related
definition), it is possible to do something that's actually
pretty convincing.
is in the interior of the
angle CBD, in order to apply the result about
angle addition. Under our approach it isn't too difficult.
It may require some thinking, but if you go back to the definition of
interior of an angle (and maybe another related
definition), it is possible to do something that's actually
pretty convincing.
![]() be
the orthocenter. The question is to find explicit formulas
for r, s and t.
be
the orthocenter. The question is to find explicit formulas
for r, s and t.
![]() , let
Q be the midpoint of
, let
Q be the midpoint of
![]() , and let
R be the midpoint of
, and let
R be the midpoint of
![]() .
.
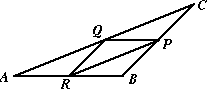
![]() is parallel to
is parallel to
![]() .
.
Suggestion: Using appropriate coordinate vectors for
P and Q, find a direction
indicator for ![]() and compare it with one of the usual direction indicators for
and compare it with one of the usual direction indicators for
![]() .
.
![]() is parallel to
is parallel to ![]() and that
and that
![]() is parallel to
is parallel to
![]() .
.
![]() | =
1/2 |
| =
1/2 |![]() |
|
![]() | =
1/2 |
| =
1/2 |![]() |
|
![]() | =
1/2 |
| =
1/2 |![]() |
|
|![]() | = v |
| = v |![]() |
|
|
|![]() | = v |
| = v |![]() |
and
|
|
and
|![]() | = v |
| = v |![]() |.
|.
![]() ABC, then the orthocenter of triangle PQR is (r,s,t)
ABC, then the orthocenter of triangle PQR is (r,s,t) PQR. ( We use
the notations ABC and PQR as part of
the superscript to indicate the triangle relative to which we are taking
the barycentric coordinates . . . )
PQR. ( We use
the notations ABC and PQR as part of
the superscript to indicate the triangle relative to which we are taking
the barycentric coordinates . . . )
Suggestion: Refer to the formula from Theorem 7 of Chapter 3
of the text. What power of v can be factored from
the numerators and from the denominators?
![]() be the orthocenter of triangle
ABC.
be the orthocenter of triangle
ABC.
Suggestion: Consider the given information as being a
formula for the coordinate vector of the orthocenter, namely
rA + sB + tC. Working with the other
results we have obtained, try to develop a formula for the coordinate
vector of the circumcenter.