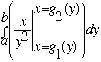Math 5335: hints for the Dec 4 and Dec 11 HW

Math 5-335 Fall 2003
Hints for the December 4 and and December 11 homework

Suggestion (If this isn't your very first visit to this page, then please click the "reload" or "refresh" button on your browser window. This page may be updated again in the next few days.)

Hint for exercise #9 in §7.9 I'll give a re-wording of the problem, which may help to reduce some of the confusion related to understanding what the problem is all about. In doing this, I'll start by introducing some terminology. Thus, if we're given an incidence geometry, i.e., a model of the indicence axioms I1, I2, I3 we'll define the "dual geometry" as follows:

A dual point is a line in the original geometry;
A dual line is a point in the original geometry;
The definition of incidence is unchanged, i.e., a dual point and a dual line are incident if and only if the corresponding line and point are incident in the original geometry. I'm using the quotation marks because the dual model doesn't always satisfy the incidence axioms. For instance, if parallel lines exist in the original geometry, then axiom I1 doesn't hold for the dual model. {But you don't need this observation to work the problem ... }

Now, here's the promised re-wording:
Show that if we start with the 7-point geometry from §7.2, then the resulting dual geometry satisfies the axioms I1, I2, I3.

Well, that's the main point, actually. But if we want to expand on it slightly, we can say that the following statements need to be proved:

(I1) Given 2 dual points, there's a unique dual line incident with both.
(I2) Every dual line is incident with at least 2 dual points.
(I3) There exist 3 dual points such that no dual line is incident with all 3 of them. Anyway, the first step is to translate these statements into statements about the original geometry: for "dual line" we substitute __________, and for "dual point" we substitute ___________. {Please fill in the blanks.} Then the second step is to prove the resulting statements, either by using the axioms and/or results of other exercises, or by explicitly going through an adequate list of possibilities.

As noted in the text, you're allowed to use the result of exercise #8 without giving a proof. This could be useful in connection with proving I1 for the dual geometry . . .

One final comment: You're not required to use the terminology introduced here, for instance if you were able to correctly formulate the necessary statements by just looking at things directly.

Hint for exercise #44 in §7.9 Sometimes there's more than one way to organize the proof of an "if and only if" statement. One way that works fairly well here is to prove the following two statements:

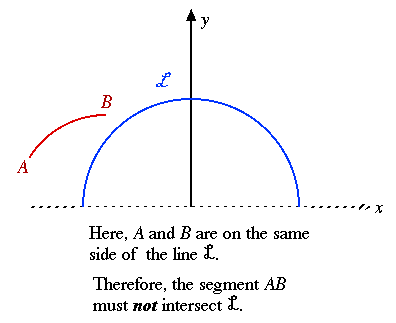
If the points A and B are on opposite sides of the line L, then the segment 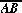intersects L.
If the points A and B are on the same side of the line L, then the segment 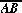does not intersect L.

Of course, the notation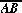

refers to the Poincaré segment joining A and B. If the two points happen to have the same x-coordinate, then the Poincaré segment will be the same as the corresponding Euclidean segment, but otherwise it will be the a specific circular arc that has A and B as its endpoints.

I'll focus my comments mainly on the case where L is a curved Poincaré line. Suppose that that the equation of L is
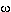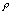(x - )² + y² = ².
Then one side of L is (by definition) given by the inequality (x - 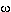)² + y² - 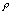² > 0, while the other side is given by the opposite inequality. Now, we represent the segment 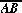parametrically. If A and B have the same x-coordinate, then this will be x = (constant), y = t, for t in some specific interval. If A and B have distinct x-coordinates, then it will be a trigonometric parametrization with the parameter, say t, running through some closed interval. {But the center and radius that are involved likely will be different from 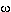and .}

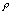Anyway, we substitute from the parametrization to express (x - 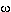)² + y² - 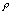² > 0, as a function of the parameter t on the appropriate interval. If things are set up correctly, then in proving the first statement, you'll find that this quantity is positive at one end of the interval and negative at the other endpoint, and is a continuous function of the parameter t. So, we have a setup where we can apply the Intermediate Value Theorem.

For proving the second statement, things are slightly more delicate. We'll find that our function (the same one as in the other part) is either positive at both ends of the interval, or negative at both ends of the interval. We'd like to claim that it's also nonzero at all other points of the interval, but the Intermediate Value Theorem is of no help whatsoever in this kind of situation. Instead, the strategy is to show that the function is monotonic (either strictly increasing or strictly decreasing) on the interval in question. We have to use the specific form of our function, namely that it's obtained by substituting from our parametrization into the expression x - 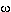)² + y² - 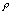². Alternatively, an approach to establishing monotonicity without actually using parametrizations seems to be the point of Lemma 3 in §7.3.

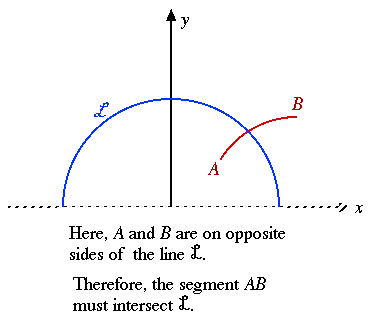
The following diagrams should give some indication of what the basic concepts are about.
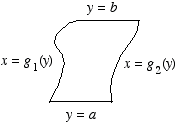
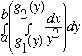