Hint for §3.12, problem 64
(Re-written retroactively)
Here's a diagram of the setup:
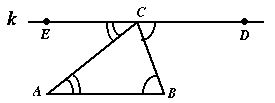 According to the plan presented in the text
we're given that D and E
are on the line k through C
parallel to
According to the plan presented in the text
we're given that D and E
are on the line k through C
parallel to 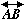 and further
that A and D are on opposite sides of
and further
that A and D are on opposite sides of
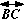 while
B and E are on opposite sides of
while
B and E are on opposite sides of
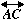 . Under this setup, we need to
prove that
. Under this setup, we need to
prove that 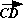 and
and
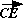 are opposite rays, so that
we can apply Proposition 34 of Chapter 1 [about complementary angles].
We can reformulate the question about opposite rays as being about
whether D - C and E - C are
negative scalar multiples of each other. Since we're given that
k is parallel to
are opposite rays, so that
we can apply Proposition 34 of Chapter 1 [about complementary angles].
We can reformulate the question about opposite rays as being about
whether D - C and E - C are
negative scalar multiples of each other. Since we're given that
k is parallel to
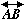 , it is possible to
compare either D - C or E - C
with B - A, determining
in each case whether the vector in question is a scalar multiple of
B - A, with a positive coefficient or with a
negative coefficient.
, it is possible to
compare either D - C or E - C
with B - A, determining
in each case whether the vector in question is a scalar multiple of
B - A, with a positive coefficient or with a
negative coefficient.
Now, the text says that the only other loose end is about showing that
A and B are on the same side of
k. Actually, in the application of
Proposition 33 of Chapter 1 [about addition of angular measure],
one needs to check that B is in
the interior of angle
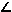 ACD. Showing
that A and B are on the same side of
k is part of this. But it also involves
showing that B and D are on the
same side of
ACD. Showing
that A and B are on the same side of
k is part of this. But it also involves
showing that B and D are on the
same side of 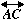 .
What was proved about oppositeness of rays in the other part of the
problem can be very helpful here.
.
What was proved about oppositeness of rays in the other part of the
problem can be very helpful here.
Comments and questions top;
roberts@math.umn.edu
Back to to the homework list.
Back to the class homepage.
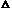 = -A +2B =
B - (A - B)
= -A +2B =
B - (A - B)
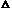 = -A +2C =
C - (A - C).
(By Theorem 16 in Chapter 2, these points should be on the lines
= -A +2C =
C - (A - C).
(By Theorem 16 in Chapter 2, these points should be on the lines
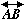 and
and
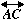 respectively.
respectively.
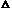 is on this line if and only if r = -1.
is on this line if and only if r = -1.
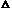 and (a,0,-a+1)
and (a,0,-a+1)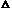 .
.
