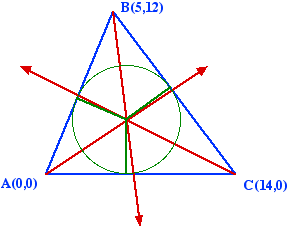
Supplementary problem #3   Consider the triangle shown in the following figure:

1. Find the barycentric coordinates of the incenter, and then find the rectangular coordinates of the incenter.
2. Find the point of the segment    that is closest to the incenter, and find the inradius (radius of the inscribed circle).
3. Then find the points of the segments    and    that are closest to the incenter. Label all 3 of these points of tangency on a copy of the diagram.
4. Find the points where the angle bisectors cross the opposite sides of the triangle, and label all 3 of these points on the same copy of the diagram that you used in part c.
     

Supplementary exercise #4   Given triangle   ABC,   let   P   be the midpoint of , let   Q   be the midpoint of , and let   R   be the midpoint of .
 
        

1. Show that is parallel to .
   Suggestion: Using appropriate coordinate vectors for   P   and   Q,   find a direction indicator for and compare it with one of the usual direction indicators for .
2. Similarly, show that is parallel to and that is parallel to .
3. Using the vector formulas developed on parts a and b -- or by any other valid method -- verify the following equalities of lengths of segments:
   • || = ¹/₂ ||
   • || = ¹/₂ ||
   • || = ¹/₂ ||
4. Show that the circumcenter of triangle   ABC   is equal to the orthocenter of triangle   PQR.
   Suggestion:   Suppose that we draw the perpendicular bisector of a side of triangle   ABC.   In what role does the line that we drew function relative to triangle   PQR?   ( This is intended to be a geometry problem. In particular, it is recommended not to use the formulas given in Theorem 7, Corollary 10, and Theorem 13 of Chapter 2 -- especially because a problem in next week's assignment will be about using the result of this problem in a proof of one of those formulas. )

Supplementary exercise #5   Given triangle   ABC   and triangle   PQR. Assume that there exists a nonzero real number   v   such that:
          || = v ||    || = v ||    and    || = v ||.

Show that if the orthocenter of triangle   ABC   is   (r,s,t)^ABC,   then the orthocenter of triangle   PQR   is   (r,s,t)^PQR.    ( We use the notations   ABC   and   PQR   as part of the superscript to indicate the triangle relative to which we are taking the barycentric coordinates . . . )
 
Suggestion: Refer to the formula from Theorem 7 of Chapter 3 of the text.   What power of   v   can be factored from the numerators and from the denominators? ( It's useful to note here that the numerators and denominators in the formula given in Theorem 7 are homogeneous polynomials:   this means that all of the monomials occurring in one of these polynomials have the same total degree. For instance,   2x³ + 3y³ + 5z³ + 11xyz   is homogeneous of degree 3. )
 

Note:   The assignment also includes problems #7 and #11 from Chapter 3 of the text.