Math 5336
Spring 2004
Solutions to exercise 3.35

  1. X ~~-> -X + (4,-5,9)
    Solution:   This is a central involution, with center = .
    (To find the fixed point, we solve the equation 2X = (4,-5,9).)
      
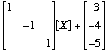  2. (x1,x2,x3) ~~-> (x1+3, -x2-4, x3-5),   or equivalently    [X] ~~-> .
    Solution:   There are no fixed points, and the matrix is a reflection matrix, so this is a glide reflection. The mirror of the reflective part has to be parallel to the plane  x2 = 0;  the glide has to be parallel to this plane. Hence, the shift vector (3,-4,-5) can be represented as a sum:  (3,-4,-5) = (3,0,-5) + (0,-4,0).  Translation by  (0,-4,0)  is perpendicular to the mirror plane, while translation by  (3,0,-5)  is parallel to the mirror plane. Therefore the glide is (3,0,-5). The reflective part is  (x1,x2,x3) ~~-> (x1, -x2-4, x3),  so that the mirror of the reflective part is the plane  x2 = -2.  (Check this by solving to find the fixed points.)
      
  3. X ~~-> (-x2,x3,-x1) + (3,-3,-3)   or equivalently   [X] ~~-> .
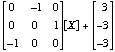    Solution:   The matrix has determinant = +1, so that it corresponds to a rotation. But there are no fixed points, so that we have a slide rotation. (To find fixed points, we would have to solve the following system:
               x1 = -x2 + 3       or       x1 + x2 = 3
               x2 = x3 - 3       or      x2 - x3 = - 3
               x3 = -x1 - 3       or       x1 + x3 = - 3,
    but if we add the 2nd and 3rd equations we get  x1 + x2 = -6,  which contradicts the 1st equation.)
    The matrix  C := has a rotation axis joining the origin and (1,-1,-1).  (Solve the equation  C[X] = [X]  to check this.) The shift vector (3,-3,-3) happens to be parallel to this, so that the axis of the rotation  is {t(1,-1,-1)}. It remains to find the angular measure of the rotation. One (non-systematic) way to do this is to calculate some powers of  C; this leads to  C3 = I,  and thus to the conclusion that the angular measure of the rotation is  2/3,  or  120º. A more systematic approach involves choosing a vector perpendicular to the rotation axis, such as  W = (1,1,0),  and then finding the angle between  [W]  and  C[W].
    Thus:  C[W] = 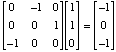, so that  = -1/2,  and the angular measure is  2/3.
      
  4. X ~~-> (-x2,x3,-x1) + (6,6,0)   or equivalently   [X] ~~-> .
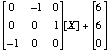    Solution:  From the previous problem, we know that this is either a rotation or a slide rotation, depending on whether or not there are fixed points. To look for fixed points, we solve the system:
               x1 = -x2 + 6       or       x1 + x2 = 6
               x2 = x3 + 6       or      x2 - x3 = 6
               x3 = -x1
    Because of the third equation, we know that the first two equations are equivalent to each other. So we have a non-empty fixed point set, and thus a rotation. Specifically, the fixed point set (and thus the axis of the rotation) is  {(3,3,0) + t(1,-1,-1)}  or equivalently  {(0,6,0) + s(1,-1,-1)}. From the previous problem, we know that the angular measure of the rotation is  2/3.
      
  5. [X] ~~-> .
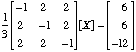    Solution:  The matrix  C = 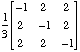has determinant = +1,  and is symmetric. Since an orthogonal matrix satisfies  CCT = I,  it follows that  C2 = I. Therefore we have either a half turn or a slide rotation, depending on whether or not there are any fixed points. To find the fixed points, we must solve the following system of equations:
              3x1 = -x1 + 2x2 + 2x3 - 18       or       -4x1 + 2x2 + 2x3 = 18
               3x2 = 2x1 - x2 + 2x3 - 18         or        2x1 - 4x2 + 2x3 = 18
               3x3 = 2x1 + 2x2 - x3 + 36        or        2x1 + 2x2 - 4x3 = -36
    Since the sum of all 3 equations is 0, we have a consistent system and thus a nonempty fixed point set. Therefore the transformation is a half turn.  After some calculation (or guessing), we find that the axis (or fixed point set) is  {(0,0,9) + t(1,1,1)}.
      
  6. [X] ~~->
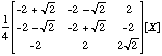
    Solution:  The determinant of this matrix  C := 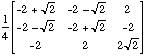 is  -1.   (I "cheated" and got some help from my computer. But if you were going to do that calculation by hand, it's best to expand along the 3rd row or 3rd column -- rather than the 1st row or 1st column -- since certain "sum and difference" patterns come into play more usefully with this "nonstandard" choice.)   Since  C  is not symmetric,  C2  is not  the identity, and we don't have a reflection here, but rather a rotatory reflection. To find the axis, we have to solve the equation  C[X] = -X.  Rather than presenting the details of the calculation, I'll just say that the axis (solution set) is  {t(1,1,0)}. (Well, it's at least easy to check that this actually works!) Finally, the mirror of the reflection (actually not requested in the problem) is the plane through the origin perpendicular to the axis: thus it is the plane  x1 + x2 = 0.
      
  7. X ~~-> 1/2(-x1 +x2, x1+x2, 16x3) + (4-4,0)   or equivalently:  
    [X] ~~-> .
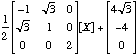    Solution:  The matrix  C := 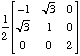 has determinant = -1. Since it is symmetric (and orthogonal), we have  C2 = I.  Hence, we have a reflection or a slide reflection, depending on whether or not there are fixed points. Without showing the calculation, I'll just mention that  (0,-8,0)  is a particular fixed point and that the general fixed points satisfy the equation  x1 - x2 = 8.

Comments and questions to:  roberts@math.umn.edu

Back to  to the class homepage.