In this section, we'll tell you how to get started, and point you toward the basic Matlab help page that explains how to do surface plots. After reading that, you probably can go directly to material on the improved approach to surface plotting. The section on useful matrix commands still includes valuable material, but it is not possible to do surface plots without understanding that material. And when you have a basic figure that you'd like to tweak, you may consul the section on manipulating the Matlab graphics window.
- We begin by starting Matlab, as usual, from the
Applications menu on the main Fedora (linux) screen. This will open two windows:
[1] the command window (where you enter Matlab commands) and [2] the help window.
The command window has a history sidebar, where you can look up commands that
you've entered in previous sessions. {You can copy one or more of those
old commands into the active command window if that seems like a good idea.}
The help window presents a topical index, which you can navigate to find
information about Matlab tools that you want to work with. {It does,
however,take some practice to get used to the way that this is set up.}
- Click to expand the "Matlab" heading in the left hand
column of the Help window (right below "Release Notes" and "Installation".
In this subsection (where the headings appear in blue) you can find
a majority of the most relevant topics if you click to expand the "Graphics"
and/or "3-D Visualization" headings.
- Under this heading the following links will be particularly
useful for us:
- Representing a Matrix as a Surface. This section explains
the idea of seting up a rectangular grid.
- Parametric Surfaces. The examples that we'll be able to
draw most effectively are surfaces that are presented parametrically.
This section includes a nice example of how to sketch one of those.
- Representing a Matrix as a Surface. This section explains
the idea of seting up a rectangular grid.
- At the very bottom of the left column there is a
link called Plotting and Visualization Function. Clicking on
this link produces an extensive list in the right column. That list,
which includes links to help text for specific commands, includes
most of the plotting commands that we're likely to need.
- To find other useful commands including commands for
working with matrices, go back to the main helpdesk window.
Under the heading "MATLAB Functions" in the left column, the link
"by Subject" usually is most effective. There are several
useful links in the window that appears next, including
Elementary Matrices and Matrix Multiplication
and Operators and Special Characters. The latter
list includes [for instance] an explanation of the very important difference
between matrix multiplication, denoted * (as expected), and array
(or elementwise) multiplication, which is denoted .* instead.
- When finished remember to close the browser window.
This will make things go a lot more smoothly the next time you run
Netscape on the math department system.
Some useful matrix commands
An improved approach to surface plotting
(under construction as of December 10, 2008)
Manipulating the Matlab graphics window
Here are some other things that you can do:
Further specific examples and sugestions
For more information. On the Matlab help page
(type helpdesk at the Matlab prompt)
Comments and questions to: roberts@math.umn.edu
Back to
the help page index.
Back to the Math 5385 class homepage.
>>
>> A = [1 2; 0 -3]
A =
1 2
0 -3
>> B = [-7 -9]
B =
-7 -9
>> C = [7 9]'
C =
7
9
(The single quote stands for "transpose").
The following is just for practice:
>>
>> C + B'
ans =
0
0
>
>> [A C]
ans =
1 2
7
0 -3
9
(Note that both must have the same number of rows).
>> [A; B]
ans =
1 2
0 -3
-7 -9
(Here, they must have the same number of columns).
>> [A C; B 0]
ans =
1 2
7
0 -3
9
-7 -9
0
the matrix of zeros. But we can create a matrix of zeros
of any specified size:
>>
>> zeros(4,2)
ans =
0 0
0 0
0 0
0 0
>>
>> ones(3,5)
ans =
1 1
1
1 1
1 1
1
1 1
1 1
1
1 1
>>
>> eye(3)
ans =
1 0
0
0 1
0
0 0
1
>>
>> A
A =
1 2
0 -3
>> B
B =
-7 -9
>> C
C =
7
9
>>
>> A*C
ans =
25
-27
>> B*A
ans =
-7 13
>> A^2
ans =
1 -4
0 9
>> A^-1
ans =
1.0000 0.6667
0 -0.3333
>>
>> A.^3
ans =
1 8
0 -27
>> B.^2
ans =
49 81
elements of another matrix. In the MATLAB help pages,
this is called array multiplication.
>>
>> B.*C
??? Error using ==> .*
Matrix dimensions must agree.
>>
>>
>> B.*C'
ans =
-49 -81
just substitute the matrix into the function command:
>>
>> sin(pi*(0:1:24)/12)
ans =
Columns 1 through 7
0
0.2588
0.5000 0.7071
0.8660
0.9659 1.0000
Columns 8 through 14
0.9659 0.8660
0.7071
0.5000 0.2588
0.0000
-0.2588
Columns 15 through 21
-0.5000 -0.7071
-0.8660 -0.9659
-1.0000 -0.9659
-0.8660
Columns 22 through 25
-0.7071 -0.5000
-0.2588 -0.0000
As usual, the goal is to draw a surface which is given
parametrically:
y = g(t,u)
z = h(t,u),
As a specific instance, let's consider the Whitney umbrella surface
(see exercise 9 in sec 3.3).
Thus, f(t,u) = t,
g(t,u) = u², and
h(t,u) = tu, so that:
y = u²
z = tu,
such as
multiplication and exponentiation.
g = 'u^2'
h = 't*u'
G = vectorize(g)
H = vectorize(h)
H = t.*u
s = -1:0.1:1;
Y = eval(G);
Z = eval(H);

s = -1:0.05:1;
[t,u] = meshgrid(r,s);
X = eval(F);
Y = eval(G);
Z = eval(H);
S = surf(X,Y,Z);
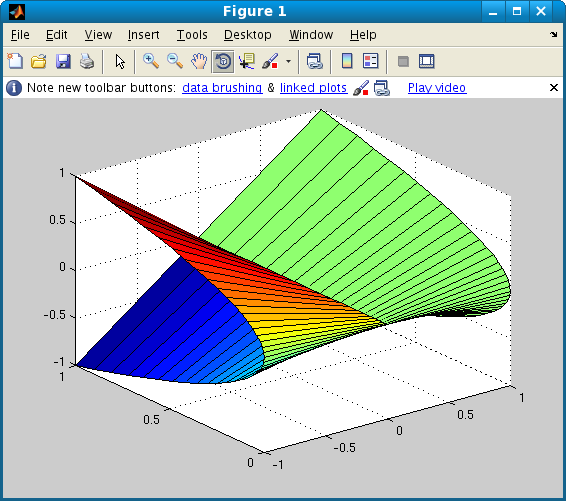
This has some desirable features, but the color of the right half is
disappointing. This is related to the default values that Matlab uses
in calculating the color data. We can, however, use Matlab's
set to substitute a matrix of our own
choice for the color data. This matrix must be of the same size as
the X, Y or Z matrices in the plot. For our ruled surface,
the u matrix is a good choice, because the lines on the surface
correspond to u-values. Accordingly, here is an appropriate
command:
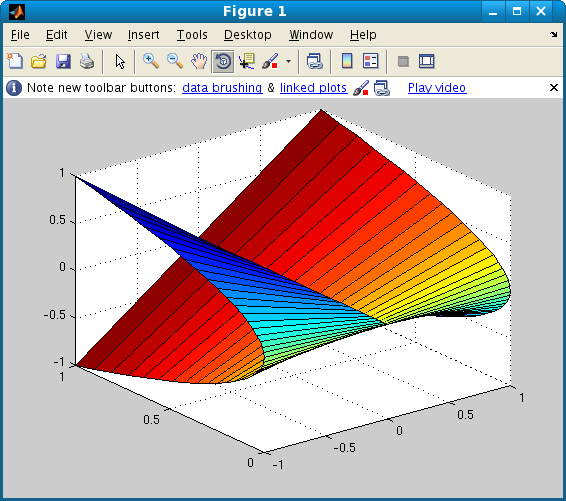
Now, it might be nice to see the surface from a different direction. To
accomplish that, we click on the rotate icon
![]() on the toolbar
and then use the mouse to rotate the figure. Among many other possibilities,
here is one position to which it can be moved:
on the toolbar
and then use the mouse to rotate the figure. Among many other possibilities,
here is one position to which it can be moved:
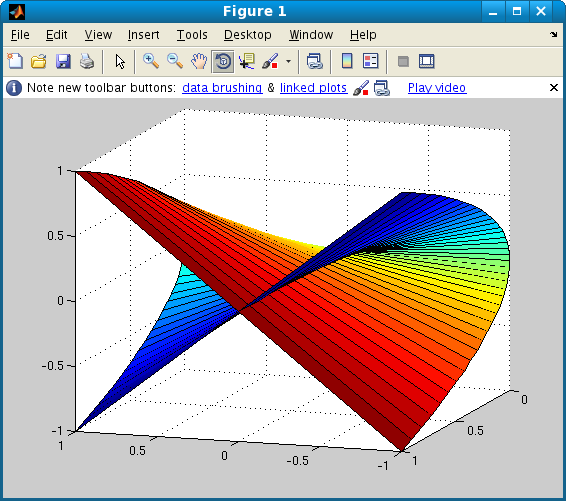
![]() and then use the mouse to rotate your figure.
and then use the mouse to rotate your figure.
![]() and then click on the figure to zoom in.
and then click on the figure to zoom in.
![]() and then click on the figure to zoom out.
and then click on the figure to zoom out.
![]() and then use various tools to add features to your figure.
and then use various tools to add features to your figure.
set(S, 'linewidth',2)
set(S, 'linestyle','none')
set(S, 'linestyle','-')
Although the first two examples below are given by trigonometric
parametrizations, they're actually algebraic surfaces -- the first one
obviously so, because of its well known equation
x2 + y2 + z2 = 1.
Any of the matlab text presented below can be copied from this window
and pasted into a Matlab command window. If desired, you can then
modify it to plot other figures.
Here is a sequence of Matlab commands which produces the drawing of the
unit sphere shown below.
The small rectangles in the grid are squares in which the length of the
side is π/24.
g = 'sin(phi)*sin(theta)'
h = 'cos(phi)'
F = vectorize(f)
G = vectorize(g)
H = vectorize(h)
%Our functions are now in the form that Matlab will need.
r = pi*(-24:1:24)/24;
%This gives a row vector (1 by 49).
s = pi*(0:1:24)/24;
%This also gives a column vector (25 by 1).
[theta,phi] = meshgrid(r,s);
%This gives theta and phi as 25 by 49 matrices.
X = eval(F);
Y = eval(G);
Z = eval(H);
%These commands evaluate our functions at the gridpoints.
The results
are stored as 25 by 49 matrices.
surf(X,Y,Z)
With the default settings, this produces a somewhat flattened looking
sphere. Click here if you would like to
see it. We can use a fairly easy matlab command to get a more symmetric
sphere, namely:
axis square
Here is the final result:

Some comments:
So, the matrices don't appear on our computer screen.
(But we don't need semicolon in the line that produces
the graphics window ... )
The mathematical aspects here are relatively standard; this example
also exhibits a method of manipulating the graphics window
to produce aobetter sketch. The torus that we will plot is obtained by
rotating (about the z-axis) the circle in the yz-plane with center (0,2,0)
and radius 1, as shown in the figure.

So, the z-coordinate of a point on the circle is given by the formula
z = sin(φ),
and its distance from the z-axis (equal to the y-coordinate in this
cross section is given by the formula
r = 2 + cos(φ).
If we describe our torus parametrically in cylindrical coordinates,
it is then given as follows:
s = pi*(-24:1:24)/24;
[theta phi] = meshgrid(r,s);
f = '(2 + cos(phi))*cos(theta)';
g = '(2 + cos(phi))*sin(theta)';
h = 'sin(phi)';
F = vectorize(f);
G = vectorize(g);
H = vectorize(h);
x = eval(F);
y = eval(G);
z = eval(H);
surf(x,y,z)
Here's what this produces:

The figure is literally correct, but the scales for the various axes
(the defaults chosen by Matlab) make the figure look out of proportion.
The "cheapest" way to fix this is by changing the size
of the graphics window -- just grab the lower right corner with the
mouse, using the left button.
Click here to see a (slightly cropped)
picture of what we can accomplish in this way. Alternatively,
we can get a similar (but somewhat smaller) result by using the Matlab
command axis square
Another way to fix the scaling problem is by editing the
axes properties, found under the Tools menu
at the top of the graphics window. For instance, if the x and y limits
are set to run from -3 to 3, and the z limits are set to run from -1.5
to 1.5, then we get a pretty credible sketch with the original window
size. [To change any number in the dialog box,
click the corresponding "manual" button.] To see the result of this
process, click here.
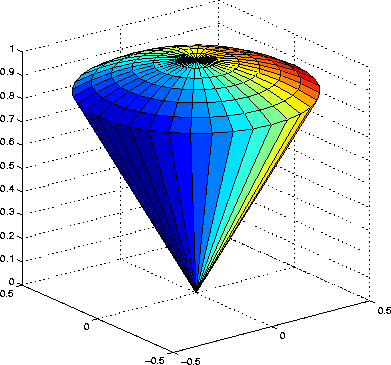
Sometimes a picture of a surface has to be drawn in two pieces because
various parts are described by different parametric formulas. That's the
case here, since one part is a portion of a sphere while the other part
is a portion of a cone. So, this example shows the use of the Matlab
command "hold on", which makes it possible for previously drawn parts of
the picture to remain while new parts are added. (If you make a mistake,
then the command "hold off" makes it possible to start over.)
We use spherical coordinates, by means of the usual formulas:
x = ρ sin(φ) cos(θ),
y = ρ sin(φ) sin(θ),
z = ρ cos(φ),
and we begin by drawing a cone, such that a generating line segment has
length = 1 and makes an
angle of π / 6
radians with the positive z-axis. Therefore, φ has a constant
value, namely π / 6. We'll
approximate the cone with triangular pieces with one vertex at the origin,
but they're actually drawn as rectangles, with two vertices
at the origin. So, here's a series of Matlab commands that will implement
this:
rho = [0 1]';
x = rho*cos(theta)*sin(pi/6);
y = rho*sin(theta)*sin(pi/6);
z = rho*ones(size(theta))*cos(pi/6);
cone = surf(x,y,z);
axis square
The resulting picture has a fairly monotonous coloring, but we can vary
the color in a fairly nice way by using a new matrix of color data:
set(cone,'CData',c1)
Now, we "freeze" the picture so that new material can be added:
The next order of business is to draw an appropriate piece of spherical
surface on top of the cone. This time, it is ρ that has a constant
value, namely ρ = 1. So, we simply leave rho out of the formulas.
X = sin(phi)*cos(theta);
Y = sin(phi)*sin(theta);
Z = cos(phi)*ones(size(theta));
cap = surf(X,Y,Z);
set(cap,'CData',c2)
Here is the final result:
see the following items under the MATLAB topics menu:
(In the new table of contents that comes up, scroll down a ways
to find Creating 3-D Graphs.
Under that topic, there's a special link about Parametric Surfaces.).
many of these
from the Matlab command window. For instance, with the surface example
above, we can type:
set(S,'meshstyle','column') This gives us lines in just 1 direction,
rather than a grid. Another version
is: set(S,'meshstyle','column')To get the grid back, type
>> set(S,'meshstyle','both')
Changing colors is also possible, but somewhat more elaborate.