Math 8203 (Algebraic Geometry)
Fall 1997
The Zariski Topology and Regular Functions
Copyright (©) 1997 by Joel Roberts.
Contents
Let X be a variety. Thus, we can be considering X
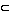 An or X
An or X
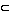 Pn.
In either case, we claim that the subsets of X
which are algebraic (as subsets of
An or
Pn
respectively) are the closed sets of a topology. In order to
verify this fact, it is clearly sufficient to consider the case where X is
An or
Pn itself.
Pn.
In either case, we claim that the subsets of X
which are algebraic (as subsets of
An or
Pn
respectively) are the closed sets of a topology. In order to
verify this fact, it is clearly sufficient to consider the case where X is
An or
Pn itself.
PROOF IN THE AFFINE
CASE. We have V(0) =
An while
V(1) is empty. If Xa =
V(Sa), where a runs through
some index set and the Sa
are subsets of
K[x1,
...,xn], then:
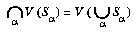
Thus, an arbitrary intersection of algebraic sets is algebraic. To show that a finite
union of algebraic sets is algebraic, the key step is to understand the union of two algebraic
sets. So, if X1 =
V(S1) and
X2 =
V(S2), then we can check
that X1 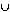 X2 = V(T)
where:
X2 = V(T)
where:
T = {fg | f in S1 and g in
S2 }.
The key step is to observe that if p lies in V(T) but
p is not in X1 , then
f(p) is nonzero for some f0
in S1. Since f0(p)g(p) = 0 for every g in
S2, it follows that p is a
point of X2.
THE NOETHERIAN
PROPERTY. By definition, a topological space is
Noetherian if every descending sequence of closed subsets
eventually stabilizes. Thus, if:
X1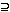 X2
X2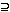 . . .
. . .
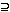 Xk
Xk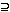 Xk+1
Xk+1
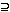 . . . ,
then there exists M such that
XM = XM+1 = . . .
. . . ,
then there exists M such that
XM = XM+1 = . . .
PROPOSITION. The Zariski topology is
Noetherian.
Before proving this in the affine case, we state and prove a lemma.
LEMMA. Every algebraic set in
An is of the form
X = V(I), where I is an ideal in
K[x1,
...,xn].
TO PROVE THE LEMMA, we show that if S is a subset of
K[x1,
...,xn],
then V(S) = V(I), where I is
the ideal generated by S. This follows from the observation
that elements of I are sums of the form:
g1f1
+ . . . + gmfm ,
with m varying, fj in S and
gj
in K[x1,
...,xn].
TO PROVE THE PROPOSITION,
we consider a descending sequence:
X1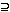 X2
X2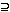 . . .
. . .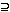 Xk
Xk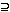 Xk+1
Xk+1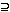 . . . ,
with Xk =
V(Ik).
We may not have started with an ascendending sequence of
ideals, but can arrange that by noting that
Xk =
V(Jk),
where Jk
= I1 + ...
+ Ik .
Note that Xk =
X1
. . . ,
with Xk =
V(Ik).
We may not have started with an ascendending sequence of
ideals, but can arrange that by noting that
Xk =
V(Jk),
where Jk
= I1 + ...
+ Ik .
Note that Xk =
X1 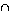 ...
... 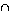 Xk .) We now have an
ascending sequence of ideals:
J1
Xk .) We now have an
ascending sequence of ideals:
J1 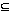 J2
J2
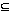 . . .
. . . 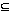 Jk
Jk
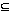 Jk+1
Jk+1 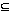 . . .
It is known that K[x1,...,xn] is
Noetherian, so that every ascending sequence of ideals eventually stabilizes. Therefore our
descending sequence of closed subsets also does.
. . .
It is known that K[x1,...,xn] is
Noetherian, so that every ascending sequence of ideals eventually stabilizes. Therefore our
descending sequence of closed subsets also does.
DISTINGUISHED OPEN
SETS (AFFINE CASE). If f is an element of the polynomial ring
K[x1,...,x
n], we define:
D(f) = {p | p lies in
An
and f(p) is nonzero}
This is clearly an open subset, since D(f) is the complement in
An of the closed set
V(f). These are of interest because of the following result.
PROPOSITION. The family of distinguished open sets
is a basis of the Zariski topology of An.
PROOF. Every ideal is a sum of principal ideals.
Therefore, the closed set V(I) is the intersection of closed sets
V(f), where f runs through some set of generators. Therefore
the complement of V(I) is the union of the distinguished open sets
V(f).
Let X be a variety, and let U be an open subset. If
f is a K-valued function defined on U, we will say
that f is regular at a point p of U if there is an
open neighborhood V on which f is expressible as a quotient of
polynomials f = g/h, where h(p) is nonzero. We say that
f is regular on U if it is regular at every point of
U.
FOR INSTANCE:
- Let X = A2
. Then f(x,y) = (x + y)/
(x2 + 3xy)
is regular on the open set U = D(x2 +
3xy ).
- Let X = V(xy - zw) in A
3. We define two functions:
- f1(p) = x/z
on the distinguished open set D(z);
- f2(p) = y/w
on the distinguished open set D(w).
Now, let U = D(z) 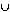 D(w). Since xy - zw = 0 at every point of X, we
have x/z = y/w at points of D(z)
D(w). Since xy - zw = 0 at every point of X, we
have x/z = y/w at points of D(z)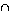 D(w). Therefore,
f1 and
f2
can be "glued together" to give a function f which is
regular at every point of U.
D(w). Therefore,
f1 and
f2
can be "glued together" to give a function f which is
regular at every point of U.
SOME RINGS ASSOCIATED TO AN AFFINE
VARIETY: If X and U are as
above, we define  (U)
to be the set of
regular functions on U. It is a commutative ring,
since we can add and multiply the values of functions. We will usually
call
(U)
to be the set of
regular functions on U. It is a commutative ring,
since we can add and multiply the values of functions. We will usually
call  (U) by its
obvious name, specifically the ring of regular functions
on U. As a particular case we have
(U) by its
obvious name, specifically the ring of regular functions
on U. As a particular case we have
 (X), the ring of
globally regular functions on X.
(X), the ring of
globally regular functions on X.
On the other hand, for X 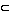 An,
we define the coordinate ring of
X to be the quotient A(X) = K[x
1,
...,xn]/I(X),
where I(X) is the defining
ideal of X.
An,
we define the coordinate ring of
X to be the quotient A(X) = K[x
1,
...,xn]/I(X),
where I(X) is the defining
ideal of X.
We have a map K[x1
,...,xn] -
>  (X), by evaluating
polynomials at points of X. One checks easily that this
is a homomorphism. The kernel is exactly I(X),
which follows easily from the definition of I(X).
Therefore, we at least have an injective homomorphism:
(X), by evaluating
polynomials at points of X. One checks easily that this
is a homomorphism. The kernel is exactly I(X),
which follows easily from the definition of I(X).
Therefore, we at least have an injective homomorphism:
A(X) - >  (X).
More generally, let U = D(f). Then we have a homomorphism:
K[x1,
...,xn,
1/f] - >
(X).
More generally, let U = D(f). Then we have a homomorphism:
K[x1,
...,xn,
1/f] - >  (U),
by evaluating expressions of the form
g/fd
at points of U. This provides an injective
homomorphism
A(X) [1/f] - >
(U),
by evaluating expressions of the form
g/fd
at points of U. This provides an injective
homomorphism
A(X) [1/f] - >  (U).
To give a naïve but rigorous definition of A(X) [1/f]
we can observe that:
K[x1,
...,xn,
1/f]
(U).
To give a naïve but rigorous definition of A(X) [1/f]
we can observe that:
K[x1,
...,xn,
1/f] 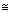 K[x
1,...,xn
+ 1]/(1 - xn +
1f(x1,
...,xn))
so that:
A(X) [1/f] =
K[x1,
...,xn +
1]/(I(X) + (1 - xn
+ 1f)).
K[x
1,...,xn
+ 1]/(1 - xn +
1f(x1,
...,xn))
so that:
A(X) [1/f] =
K[x1,
...,xn +
1]/(I(X) + (1 - xn
+ 1f)).
As observed in the text (with appropriate sketches), we can understand this
isomorphism geometrically by observing that
if X 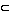 An, then we have a
bijective correspondence between D(f) and the subvariety Y
An, then we have a
bijective correspondence between D(f) and the subvariety Y
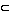 An,
whose defining ideal is:
An,
whose defining ideal is:
(I(X) + (1 - xn +
1f)).
The map is given by:
(x1,
...,xn) -
> (x1,
...,xn ,
1/f(x1,
...,xn)).
THE LOCAL RING AT A POINT. Let
p be a point of an affine variety X. We define the local
ring of X at p to be the set  X,p of germs of regular
functions at p. By definition, a germ is represented by a pair,
(U,g), where U is an open neighborhood of p,
and g is regular on U. Two pairs (U,g), and
(V,h) represent the same germ if g and h agree on
some open neighborhood of p contained in U«V.
If we think about it briefly, we see that germs can be added and
multiplied in a natural way, so that
X,p of germs of regular
functions at p. By definition, a germ is represented by a pair,
(U,g), where U is an open neighborhood of p,
and g is regular on U. Two pairs (U,g), and
(V,h) represent the same germ if g and h agree on
some open neighborhood of p contained in U«V.
If we think about it briefly, we see that germs can be added and
multiplied in a natural way, so that  X,p is
indeed a commutative ring.
X,p is
indeed a commutative ring.
A basic property of  X,p
is that the set of nonunit (or equivalently, noninvertible)
elements in
X,p
is that the set of nonunit (or equivalently, noninvertible)
elements in  X,p is an ideal.
Specifically, the germ represented by (U,g) is invertible
if and only if g(p) is nonzero: the inverse is
represented by 1/g (on a possibly smaller neighborhood).
Hence the nonunit elements are represented by germs
(U,g) such that g(p) = 0.
The germs of functions which vanish at p obviously form an ideal.
This property of
X,p is an ideal.
Specifically, the germ represented by (U,g) is invertible
if and only if g(p) is nonzero: the inverse is
represented by 1/g (on a possibly smaller neighborhood).
Hence the nonunit elements are represented by germs
(U,g) such that g(p) = 0.
The germs of functions which vanish at p obviously form an ideal.
This property of  X,p
is one way to characterize a ocal ring:
X,p
is one way to characterize a ocal ring:
PROPOSITION. Let  be a commutative ring with 1. Then the following statements are
equivalent:
be a commutative ring with 1. Then the following statements are
equivalent:
- The set of nonunit elements in
 is an
ideal.
is an
ideal.
-
 has exacly one maximal ideal.
has exacly one maximal ideal.
THE PROOF that (1)
implies (2) involves the observation that an ideal in a commutative ring with 1 which is
distinct from the unit ideal consists entirely of nonunit elements. To prove that (2) implies
(1), let m be the unique maximal ideal, and let a be a
nonunit element. Then (a) is a nonunit ideal, which is contained in some
maximal ideal, by Zorn's lemma (etc. ...). So, (a) 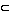 m, which forces
m to coincide with the set of nonunits.
m, which forces
m to coincide with the set of nonunits.
A SPECIFIC CASE. Let
X = An.
For any p in
An,
elements of  An,
p can be identified as quotients of
polynomials:
An,
p can be identified as quotients of
polynomials:
f(x1,
...,xn)/
g(x1,
...,xn),
where g(p) is nonzero.
The set of quotients of this type obviously is a subring of the
fraction field of K[x1,
...,xn].
This fraction field is called the field of rational functions
in n variables and denoted as follows:
K(x1,
...,xn) =
frac(K[x1,
...,xn])
FOR A GENERAL
AFFINE VARIETY
X 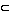 An, we also can
identify elements of
An, we also can
identify elements of  X,p
as quotients of the form f/g where
f and g are elements of the coordinate ring A(X)
and g(p) is nonzero, provided that we do the following:
X,p
as quotients of the form f/g where
f and g are elements of the coordinate ring A(X)
and g(p) is nonzero, provided that we do the following:
- identify elements of the coordinate ring as regular functions on
X by means of the inclusion of A(X) in
 (X) discussed above;
(X) discussed above;
- consider two quotients
g1/
h1 and
g2/
h2 as being equal
if and only if there exists f in
A(X) such that f(p) is nonzero and:
f(g1
h2 -
g2
h1) = 0.
While we can consider condition (2) as a technical algebraic
condition that adapts the
construction of field of fractions to a situation where
zerodivisors may exist, it also has the
intuitive content of saying that the difference of the two quotients
g1/
h1 -
g2/
h2 vanishes identically in some neighborhood of p, specifically D(f).
TO VERIFY THAT this set of quotients is a ring, we work formally
with the set of
ordered pairs and the equivalence relation between two pairs
(g1,
h1) and
(g2,
h2) given as in condition (2).
This involves some calculations, but they
are fairly routine except for transitivity. Thus, suppose that
g1/
h1 =
g2/
h2 and
g2/
h2 =
g3/
h3 as formal quotients.
Then f( g1
h2 -
g2
h1) = 0
and f* (g1
h2 -
g2
h1) = 0
in A(X), where f and f*
are elements such that f(p) and f*(p) are nonzero.
After some calculation, we find that:
ff*h2
(g1
h3 -
g3
h1) = 0.
¡¡Please check this for yourself!! Since
h2 is a denominator,
h2(p) is nonzero,
so that g1/
h1 =
g3/
h3 as formal quotients.
IT IS A PLEASANT
SURPRISE that the identification of  X,p
with this ring of quotients follows fairly immediately from the definitions
(or at least without major obstacles), even though we will
need the Nullstellensatz to verify the
"global" identification of A(X) and
X,p
with this ring of quotients follows fairly immediately from the definitions
(or at least without major obstacles), even though we will
need the Nullstellensatz to verify the
"global" identification of A(X) and  (X). Explicitly, we map our ring of quotients to
(X). Explicitly, we map our ring of quotients to  X,p by
sending the quotient g/h to the germ represented by (U,f),
where U = D(h) and f is given by the quotient g/h
at points of U. Surjectivity follows from the definitions (more or less). In
verifying injectivity, we use the fact that distinguished open subsets form a basis of the
topology.
X,p by
sending the quotient g/h to the germ represented by (U,f),
where U = D(h) and f is given by the quotient g/h
at points of U. Surjectivity follows from the definitions (more or less). In
verifying injectivity, we use the fact that distinguished open subsets form a basis of the
topology.
Let X 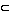 Pn be a
projective variety. There are two ways to define the concept of a
regular function on an open subset U
Pn be a
projective variety. There are two ways to define the concept of a
regular function on an open subset U
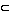 X.
These two approaches are easily seen to be equivalent.
X.
These two approaches are easily seen to be equivalent.
METHOD 1. Consider the standard affine covering
{U0,...,Un }
of Pn.
If f is defined on U 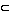 X, we say that f is regular on
U if f is regular on
U
X, we say that f is regular on
U if f is regular on
U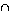 Ui
for i = 0,..., n.
Ui
for i = 0,..., n.
METHOD 2. Again, let f be defined on
U 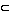 X. We say
that f is regular at a point p in U if
there is an open neighborhood V of p in
U and homogeneous polynomials
G (X0,...,
Xn) and
H (X0,...,
Xn)
with degree(G) = degree(H) such that
f(q) = G(q)/H(q) for every point
q in V.
X. We say
that f is regular at a point p in U if
there is an open neighborhood V of p in
U and homogeneous polynomials
G (X0,...,
Xn) and
H (X0,...,
Xn)
with degree(G) = degree(H) such that
f(q) = G(q)/H(q) for every point
q in V.
Explicitly, if
q = [a0,...,
an], we are requiring that
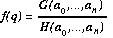
ONE CAN CHECK that the value of this expression
does not depend on the choice of homogeneous
coordinate vector used to represent q.
TO SEE WHY the two methods are equivalent,
note that the numerator and denominator in a quotient of (usual)
polynomials in
x1,...,xn
can be
"homogenized", and that we can adjust degrees by multiplying by a
suitable power of X0. For
instance, suppose that f is represented in a neighborhood
of some point of U0
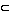 P2
by the following quotient:
P2
by the following quotient:
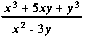 .
.
Setting x = X/Z and y = Y/Z, we transform
this into the following quotient of homogeneous polynomials:
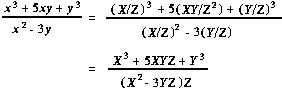
SOME RINGS
ASSOCIATED TO A PROJECTIVE
VARIETY. We can define the
local ring of germs of regular functions
 X,p at a point
p in X by methods very similar to what we did
in the affine case. So, we won't discuss the details right now.
X,p at a point
p in X by methods very similar to what we did
in the affine case. So, we won't discuss the details right now.
A concept related to the coordinate ring of an affine variety is the
homogeneous coordinate ring of a projective variety. To
get started, consider X  Pn and
define I(X) to be the ideal in
K[X0,...,
Xn] generated by all homogeneous polynomials
that vanish identically along X. We define the
homogeneous coordinate ring to be
Pn and
define I(X) to be the ideal in
K[X0,...,
Xn] generated by all homogeneous polynomials
that vanish identically along X. We define the
homogeneous coordinate ring to be
S(X) =
K[X0,...,
Xn]/I(X) .
Since homogeneous polynomials do not define regular functions on
Pn, we
do not attempt to describe elements of S(X)) as regu
lar functions on X.
A SPECIFIC INSTANCE. Let X be the twisted cubic curve in
P3. One can show that
I(X) is generated by the following three homogeneous
polynomials of degree 2 in the polynomial ring
K[W, X,Y,Z]:
- X2 - WY ,
- Y2 - XZ ,
- WZ - XY .
We won't try to verify this right now. Let's just note that it was
shown in the text (and also in class) that these polynomials vanish at
all points of the twisted cubic (and in fact that their common zeroset
is exactly the twisted cubic). Showing that they generate
I(X) requires somewhat more work.
ONE MORE
DEFINITION: We define a
quasiprojective variety to be a nonempty open subset of a
projective variety. This includes affine varieties as a special case.
The concept of a regular function is the same as in the projective
case, since the definition of regular function is essentially local.
We can work either with affine varieties or with projective varieties. Thus,
if we
consider an affine variety X
 An, we say that
X is
irreducible if it is nonempty and is not the union of two
properly smaller nonempty affine varieties. Thus:
An, we say that
X is
irreducible if it is nonempty and is not the union of two
properly smaller nonempty affine varieties. Thus:
if X = Y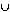 Z, where Y and Z are nonempty affine
varieties,
Z, where Y and Z are nonempty affine
varieties,
then either Y = X or Z = X.
The definition in the case of a projective variety
X
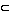 Pn
is completely parallel.
Pn
is completely parallel.
Some examples:
- A set consisting of one point is obviously irreducible.
- A1 is irreducible
Indeed, the proper closed subsets of
A1 are
finite sets, while A1 is infi
nite. (We are
assuming that our field is algebraically closed, and thus infinite.)
- By extension, any curve with a rational parametrization is irreducible
.
- An and
Pn are irreducible.
PROOF OF 4). We will consider the case of
An, since the case of
Pn is similar.Suppose
that
An =
X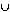 Y, where
X and Y are affine varieties, both nonempty and distinct
from
An. Let f
and g be
nonzero elements of I(X) and I(Y) respectively,
i.e. f and g are nonzero polynomials which vanish
identically along X and Y respectively. It follows that
Y, where
X and Y are affine varieties, both nonempty and distinct
from
An. Let f
and g be
nonzero elements of I(X) and I(Y) respectively,
i.e. f and g are nonzero polynomials which vanish
identically along X and Y respectively. It follows that
An =
V(f)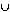 V(g),
so that
An =
V(fg).
Therefore, we can deduce the conclusion from the following:
V(g),
so that
An =
V(fg).
Therefore, we can deduce the conclusion from the following:
LEMMA. Let K be an algebraically closed
field, and let
f(x1,...,
xn)
be a nonzero element of
K[x1,...,
xn]. Then V(f)
is nonempty, and V(f) 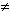 An.
An.
PROOF. We proceed by induction on n, the case
n = 1 being immediate. So, in the inductive step, we can assume (by
renumbering the variables) that
xn actually
occurs nontrivially in f. Therefore, we can write:
f(x1,...,
xn) =
g0(
x1,...,
xn-1) +
g1(
x1,...,
xn-1)
xn + ... +
gd(
x1,...,
xn-1
)
xnd,
where gi is homogeneous of
degree =
i, while d > 0 and
gd is nonzero.
By the inductive hypothesis,
there exists (a1,...,
an-1
) in
An-1 such that
gd(
a1,...,
an-1
)
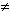 0. Hence,
0. Hence,
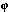 (x) :=
f (a1,...,
an-1,x) is a
nonzero polynomial of degree = d > 0. It follows that
there exist finitely many values
of an in K
such that
f(a1,...,
an) =
(x) :=
f (a1,...,
an-1,x) is a
nonzero polynomial of degree = d > 0. It follows that
there exist finitely many values
of an in K
such that
f(a1,...,
an) =
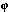 (an) = 0, and infinitely many
values of the last
coordinate such that the corresponding value of f is nonzero.
This proves our
claim.
(an) = 0, and infinitely many
values of the last
coordinate such that the corresponding value of f is nonzero.
This proves our
claim.
We note that irreducibility is really a property of closed sets in the
Zariski topology,
and does not really involve any other aspects of varieties. Here are a couple
of basic
properties of irreducible varieties.
PROPOSITION 1. If
X is an affine or projective variety, then X is
irreducible if and only if every nonempty open subset
U 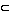 X is dense in
X.
X is dense in
X.
PROOF. Every open subset is dense if and only if every
two
nonempty open subsets have a nonempty intersection. By taking complements, this
is
equivalent to the statement that the union of two proper closed subsets is not
equal to
X.
PROPOSITION 2. Let
X 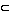 An be an irreducible
affine
variety. If X
An be an irreducible
affine
variety. If X 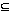 Y
Y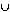 Z, where
Y and Z are affine varieties, then either X
Z, where
Y and Z are affine varieties, then either X
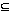 Y or X
Y or X
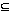 Z.
Z.
PROOF. If X
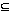 Y
Y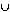 Z, then X
= (X
Z, then X
= (X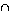 Y)
Y)
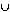 (
X
(
X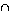 Z). By irreducibility,
Z). By irreducibility,
either X = X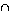 Y or X =
X
Y or X =
X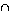 Z.
This proves our claim.
Z.
This proves our claim.
Now we can state and prove our main result.
THEOREM. Let X be an affine variety
(respectively a projective variety). Then X is the union of finitely
many
irreducible affine varieties (respectively finitely many irreducible projective
varieties).
Thus:
X =
Y1
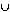 ...
...
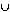 Ym,
where Y1 ,...,
Ym are irreducible.
If we require that
Yi does not contain
Yj
when i
Ym,
where Y1 ,...,
Ym are irreducible.
If we require that
Yi does not contain
Yj
when i 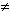 j,
then Y1 ,...,
Ym are uniquely determined.
The
corresponding statements are also true in the projective case.
j,
then Y1 ,...,
Ym are uniquely determined.
The
corresponding statements are also true in the projective case.
DEFINITION: The irreducible closed subsets which occur
in this
uniquely determined decomposition are called the irreducible components
of
X.
PROOF OF
THE THEOREM. In proving the
existence of the decomposition for Zariski closed subsets of
An, we use the fact
that the Zariski
topology of An
is Noetherian. By
definition, this means that every descending closed subsets stabilizes after fin
itely many
steps. An equivalent characterization is that every nonempty collection of
closed subsets
has a minimal member, i.e., there is a member of the collection which
is not
contained in any other set in the collection.
So, assume that there exists a Zariski-closed subset of
An which is not the
union of
finitely many irreducible closed subsets, and let S be the
collection
of closed subsets which are not finite unions of irreducibles. Then
S contains a minimal member, say
X0 .
If X0 were irreducible, this would
immediately
contradict the fact that no member of S is a union of
finitely many
irreducible closed subsets. So, we have
X0 =
Y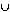 Z, where
Y and Z are proper closed subsets of
X0 .
Since X0 is a minimal member of
S, neither Y nor Z is a member of
S; therefore, both Y and Z are unions of
finitely many irreducible closed subsets. This implies that S
is a
union of finitely many irreducible closed subsets, thus contradicting the
hypothesis that
S is nonempty and thereby proving the first part of the
theorem.
Z, where
Y and Z are proper closed subsets of
X0 .
Since X0 is a minimal member of
S, neither Y nor Z is a member of
S; therefore, both Y and Z are unions of
finitely many irreducible closed subsets. This implies that S
is a
union of finitely many irreducible closed subsets, thus contradicting the
hypothesis that
S is nonempty and thereby proving the first part of the
theorem.
To prove uniqueness, suppose that some X
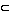 An has two different
decompositions as a union of irreducible closed subsets, both satisfying the
condition that
there be no inclusion relation among different subsets in the collection.
Specifically,
suppose that:
An has two different
decompositions as a union of irreducible closed subsets, both satisfying the
condition that
there be no inclusion relation among different subsets in the collection.
Specifically,
suppose that:
X = Y1
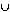 ...
... 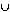 Ym
and also:
X = Z1
Ym
and also:
X = Z1
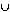 ...
...
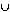 Zp ,
where there is no inclusion relation among the various Y's and also
no such
relation among the Z's.
Zp ,
where there is no inclusion relation among the various Y's and also
no such
relation among the Z's.
Consider a particular subset
Yi
from the first decomposition.
Since Yi
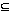 Z1
Z1
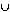 ...
...
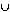 Zp, we can use Proposition 2
to show that
Yi
Zp, we can use Proposition 2
to show that
Yi
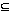 Zj for some j.
Similarly, we
show that Zj
Zj for some j.
Similarly, we
show that Zj
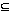 Yk for some k.
Thus,
Yi
Yk for some k.
Thus,
Yi
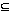 Zj
Zj
 Yk . Because there are no non
trivial
inclusions among the Y's, it follows that i = k,
and
Yi =
Zj .
Hence, all of the Yi occur
among
Z1,
... ,Zp . Now, we can show by
similar
methods that all of the Zj
occur among
Z1, ... ,
Zp .
Therefore, the same irreducible closed subsets occur in the two decompositions.
Yk . Because there are no non
trivial
inclusions among the Y's, it follows that i = k,
and
Yi =
Zj .
Hence, all of the Yi occur
among
Z1,
... ,Zp . Now, we can show by
similar
methods that all of the Zj
occur among
Z1, ... ,
Zp .
Therefore, the same irreducible closed subsets occur in the two decompositions.
Another example.
We would now like to claim that if f is an irreducible polynomial
in
n variables (respectively, if F is an irreducible homogeneous
polynomial in
n + 1 variables), then the zeroset V(f) is an irreducible
closed
subset of An
(respectively that the
zeroset V(F) is an irreducible closed subset of
Pn ). A little work
is required for
this, so that it will be saved for Exercises 7 and 8, which are linked below.
It will follow
from this claim that if f is an arbitrary polynomial in n
variables,
then the irreducible components of the hypersurface V(f) correspond
bijectively to the distinct irreducible factors of f [and similarly
in the
projective case.]
Related Exercises
Last updated November 18, 1997.
Please send comments and/or corrections to:
Joel Roberts
351 Vincent Hall
625-1076
e-mail:
roberts@math.umn.edu
http://www.math.umn.edu/~roberts
 An or X
An or X
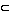 Pn.
In either case, we claim that the subsets of X
which are algebraic (as subsets of
An or
Pn
respectively) are the closed sets of a topology. In order to
verify this fact, it is clearly sufficient to consider the case where X is
An or
Pn itself.
Pn.
In either case, we claim that the subsets of X
which are algebraic (as subsets of
An or
Pn
respectively) are the closed sets of a topology. In order to
verify this fact, it is clearly sufficient to consider the case where X is
An or
Pn itself.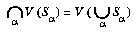
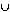 X2 = V(T)
where:
X2 = V(T)
where:
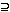 X2
X2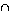 ...
... 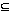 J2
J2
 (U)
to be the set of
regular functions on U. It is a commutative ring,
since we can add and multiply the values of functions. We will usually
call
(U)
to be the set of
regular functions on U. It is a commutative ring,
since we can add and multiply the values of functions. We will usually
call 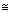 K[x
1,...,xn
+ 1]/(1 - xn +
1f(x1,
...,xn))
K[x
1,...,xn
+ 1]/(1 - xn +
1f(x1,
...,xn))
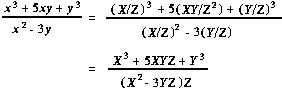
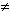 An.
An.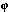 (x) :=
f (a1,...,
an-1,x) is a
nonzero polynomial of degree = d > 0. It follows that
there exist finitely many values
of an in K
such that
f(a1,...,
an) =
(x) :=
f (a1,...,
an-1,x) is a
nonzero polynomial of degree = d > 0. It follows that
there exist finitely many values
of an in K
such that
f(a1,...,
an) =