Lab 3B - Directional Derivatives, Gradients, and Vector Fields
Math 2374 - University of Minnesota
http://www.math.umn.edu/math2374
Questions to: rogness@math.umn.edu
Introduction
This week's lab is sort of a mish-mash of a few different topics which are all interrelated: directional derivatives, gradients, and vector fields. These topics are all covered in your book, but Mathematica can help you visualize them in ways not possible on a blackboard or on a written page.
When you started this class, you already knew about the plain-old single variable calculus derivative, i.e. the slope of the tangent line. Since then you've learned about two multivariable generalizations of the derivative, the "partial derivative" and the "total derivative" (which is also called the "derivative matrix" or "Jacobian matrix"). These two concepts are intertwined, of course, because the derivative matrix is composed of a bunch of partial derivatives.
In this lab, we're going to deal with variants of both of these ideas. The directional derivative is a generalization of a partial derivative. The gradient, meanwhile, is a special case of the Jacobian matrix. In what might seem to be either a bizarre coincidence or a stroke of good luck, the gradient is very useful for calculating the directional derivative. It also turns out that the gradient provides an example of a vector field, which will be an important new kind of function for the rest of the course.
If you're getting confused trying to keep track of all these connections, don't worry. You know what? This stuff is confusing! But the more you work with these ideas, the easier it gets. This lab can help, too, by showing you some visual examples, and explaining things that you've also learned about in lecture. Sometimes it can really help to read or hear a second explanation about a topic, even if the first one was very good!
With that in mind, this lab includes very few problems, but a lot of reading and a number of pictures. Above all, resist the temptation to scan over a few sentences here, gloss over this paragraph there, and just skim through the material about this or that. Gradients and vector fields, in particular, will be absolutely fundamental for the rest of the course, so it's important to learn these ideas. (That's why they're being covered in both lecture and lab.) If a sentence or paragraph is really confusing, read it over again, slowly, a few times. If you're still not sure what it says, ask your TA for help.
Directional Derivatives and Gradients
Let's go back to partial derivatives for a minute. Recall that if you're on a surface 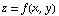 above (or below) a point
above (or below) a point 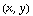 , then partial derivative of f with respect to x tells you how steep the surface is in the positive x-direction at that point. If it's positive, then the surface goes "uphill" in that direction. If it's negative, then the surface goes "downhill." The partial derivative with respect to y tells you the same sort of information about what's happening in the positive y-direction.
, then partial derivative of f with respect to x tells you how steep the surface is in the positive x-direction at that point. If it's positive, then the surface goes "uphill" in that direction. If it's negative, then the surface goes "downhill." The partial derivative with respect to y tells you the same sort of information about what's happening in the positive y-direction.
That's all fine and good, but what about any of the other directions? To carry the previous metaphor a bit further, if you're a mountain climber on a 24,000ft mountain (the surface of which could be the graph of a function), you want to know what's going on in more than just the positive x- and y-direction.
(Let's think of these directions as east and north, respectively; imagine you're looking down at the xy-plane, and think of the axes as lying on a compass. The x-axis points east, to the right, and the y-axis points up, to the north.)
Back on the mountain you're climbing, you want to know: what about northeast? Or southsouthwest? Or any of the infinitely many directions in-between? That's where the directional derivative comes in. It can tell you how steep a surface is in any given direction, and whether that "steepness" goes up or down.
Take a look at the following graph, which could represent a mountain and a valley, side-by-side in an otherwise nearly flat plain.
In[242]:=
![f[x_, y_] = 2y * Exp[-x^2 - y^2] Plot3D[f[x, y], {x, -1, 3}, {y, -2, 2}, PlotRange {-. ... #62754;15, BoxedFalse, AxesLabel {"X", "Y", "Z"}] ;](HTMLFiles/index_3.gif)
Out[242]=
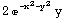
![[Graphics:HTMLFiles/index_5.gif]](HTMLFiles/index_5.gif)
Look at the point (1,0,0), which is almost exactly in the middle of the graph. A mountain climber at that point on the surface could walk either uphill or downhill -- or even in a path which keeps her flat, at the same height! Go to the following web page to see an interactive demonstration of the directional derivative using this surface:
http://www.math.umn.edu/~rogness/multivar/dirderiv.shtml
(In this online version the demonstration is included here:)
Here's what the example shows you. The green dot represents the mountain climber's position. As you change the bearing by sliding the blue dot around, you get an interactive look at the "cross section" of the surface through that point at the bearing. Now imagine fitting a tangent line to the curve representing the cross section. That's the red arrow, where the direction of the arrow shows you which direction the climber is facing.
If the arrow is pointing up, then the directional derivative in that direction is positive. If the arrow is pointing down, then the directional derivative is negative. An arrow which is pointing just ever so slightly up would indicate a small (but positive) value for the directional derivative, say 0.01. If the arrow is tilted more upward, the derivative has a much higher positive value.
As you can see, it's positive as you move from the east, through the north, to the west. From the west, to the south, and back to the east, it's negative.
Calculating Direction Derivatives
So how do we calculate direction derivatives? Well, first it's important to understand when we can even talk about them. We can only use directional derivatives for a function with one output; that is, a function 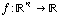 . The reason for this is that a directional derivative measures the change in that one output per unit change in some given direction on the input side of things. (In English, using the mountain climbing metaphor: the directional derivative measures the slope of the mountain, i.e. the instantaneous change in height per change in (x,y) position, where the (x,y) position is changing in some given direction.)
. The reason for this is that a directional derivative measures the change in that one output per unit change in some given direction on the input side of things. (In English, using the mountain climbing metaphor: the directional derivative measures the slope of the mountain, i.e. the instantaneous change in height per change in (x,y) position, where the (x,y) position is changing in some given direction.)
In most cases, we'll only work with directional derivatives for functions 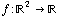 , in other words, functions like
, in other words, functions like 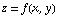 . But you could use the same ideas to calculate a directional derivative for a function
. But you could use the same ideas to calculate a directional derivative for a function 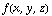 , or
, or 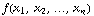 .
.
Like all derivatives, the directional derivative has a limit definition, which you can find in your textbook. It's got vectors in it, so it's a little messier than your normal, everyday limit definition of 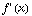 in single variable calculus, and we're going to forget about it here. Instead we'll concentrate on a different way to calculate the directional derivative.
in single variable calculus, and we're going to forget about it here. Instead we'll concentrate on a different way to calculate the directional derivative.
Suppose we've got a function 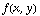 , and we're interested in the point
, and we're interested in the point 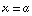 . In the example above, this was the point (1,0), but it could be anything. Now suppose we want to look in a certain direction, whether it's east, west, or 8.29 degrees west of southsouthwest. We specify a direction by choosing a vector. For example, we'd say "in the direction of the vector (3,4)." In that case, we can easily find the directional derivative of
. In the example above, this was the point (1,0), but it could be anything. Now suppose we want to look in a certain direction, whether it's east, west, or 8.29 degrees west of southsouthwest. We specify a direction by choosing a vector. For example, we'd say "in the direction of the vector (3,4)." In that case, we can easily find the directional derivative of 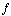 at the point
at the point 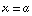 .
.
Theorem: The directional derivative of 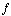 at the point
at the point 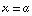 , in the direction of a vector
, in the direction of a vector ![Overscript[v, ⇀]](HTMLFiles/index_18.gif) , is given by
, is given by
![D_Overscript[u, ⇀] f(a) = Overscript[∇, ⇀] f(a) · Overscript[u, ⇀]](HTMLFiles/index_19.gif) ,
,
where ![Overscript[u, ⇀]](HTMLFiles/index_20.gif) is a unit vector in the direction of
is a unit vector in the direction of ![Overscript[v, ⇀]](HTMLFiles/index_21.gif) , given by
, given by ![Overscript[u, ⇀] = Overscript[v, ⇀]/(|| Overscript[v, ⇀] ||)](HTMLFiles/index_22.gif) , and
, and ![Overscript[∇, ⇀] f(a)](HTMLFiles/index_23.gif) is the gradient of
is the gradient of 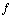 evaluated at the point a.
evaluated at the point a.
One thing in that theorem requires some explanation, namely the "gradient of f at the point a. For a function 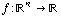 with just one output, the gradient of f is:
with just one output, the gradient of f is:
![Overscript[∇, ⇀] f = (∂f/∂x_1, ∂f/∂x_2, …, ∂f/∂x_n)](HTMLFiles/index_26.gif)
In most cases, we'll only work with two or three dimensions, in which case, ![Overscript[∇, ⇀] f = (∂f/∂x, ∂f/∂y)](HTMLFiles/index_27.gif) or
or ![Overscript[∇, ⇀] f = (∂f/∂x, ∂f/∂y, ∂f/∂z)](HTMLFiles/index_28.gif) , respectively.
, respectively.
Note how similar the gradient is to the Jacobian matrix. Write down the definitions for the Jacobian matrix of a function 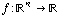 . The only real difference is whether we think of it as a vector or a 1-column matrix; the entries themselves are exactly the same!
. The only real difference is whether we think of it as a vector or a 1-column matrix; the entries themselves are exactly the same!
Why, you might ask, do we have two names for the identical thing? That's a good question, and probably has more to do with traditions -- and the difficulty of changing traditions -- than anything else.
Mathematica can compute gradients using the Grad function:
In[244]:=
![f[x_, y_, z_] = x^2 + y^2 - z Grad[f[x, y, z]]](HTMLFiles/index_30.gif)
Out[244]=
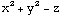
Out[245]=
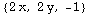
There's a catch, unfortunately; Mathematica only works with three dimensional gradients. Notice how it tacks on an extra zero at the end of the following gradient.
In[246]:=
![f[x_, y_] = x^2 + y^3 Grad[f[x, y]]](HTMLFiles/index_33.gif)
Out[246]=
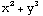
Out[247]=
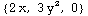
We've defined a special command called Grad2D to let you compute two dimensional gradients:
In[248]:=
![Grad2D[f[x, y]]](HTMLFiles/index_36.gif)
Out[248]=
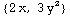
Example
Let's use the same function as before, and find the directional derivative at the point (1,0) in the direction of the vector (3,4).
In[249]:=
![f[x_, y_] = 2y * Exp[-x^2 - y^2]](HTMLFiles/index_38.gif)
Out[249]=
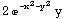
From our handy-dandy theorem, we know that:
![D_Overscript[u, ⇀] f(a) = Overscript[∇, ⇀] f(a) · Overscript[u, ⇀]](HTMLFiles/index_40.gif)
First we should compute ![Overscript[u, ⇀]](HTMLFiles/index_41.gif) , which is a unit vector in the direction of the vector
, which is a unit vector in the direction of the vector ![Overscript[v, ⇀]](HTMLFiles/index_42.gif) =(3,4). We can use the formula
=(3,4). We can use the formula ![Overscript[u, ⇀] = Overscript[v, ⇀]/(|| Overscript[v, ⇀] ||)](HTMLFiles/index_43.gif) , where the double bars mean "length of" a vector, which is also called the "norm" of a vector.
, where the double bars mean "length of" a vector, which is also called the "norm" of a vector.
In[250]:=
![u = {3, 4}/Sqrt[3^2 + 4^2]](HTMLFiles/index_44.gif)
Out[250]=
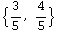
We can do that a little more automatically by defining a function like this, which will take a vector and return a unit vector in that direction.
In[251]:=
![unitvec[v_] = v/Norm[v] u = unitvec[{3, 4}]](HTMLFiles/index_46.gif)
Out[251]=
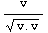
Out[252]=
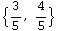
We also need the gradient of f, and then we're ready to compute:
In[253]:=
![gradf[x_, y_] = Grad2D[f[x, y]] gradf[1, 0] u gradf[1, 0] . u](HTMLFiles/index_49.gif)
Out[253]=
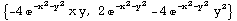
Out[254]=
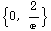
Out[255]=
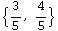
Out[256]=
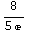
So the slope in that direction is about 8/(5e), or about 0.59. If you look back at the interactive example, does that seem correct?
From the picture it seems the steepest the incline can be is when the bearing is about northnorthwest, or (roughly) in the direction of the vector (-1,2). In that direction, the directional derivative is:
In[257]:=
![u = unitvec[{-1, 2}] gradf[1, 0] . u N[%]](HTMLFiles/index_54.gif)
Out[257]=
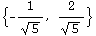
Out[258]=
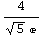
Out[259]=
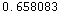
Our eyes weren't deceiving us -- it really is steeper in that direction. If you go in the direction of (-1,-1) instead, you'll go downhill:
In[260]:=
![u = unitvec[{-1, -1}] gradf[1, 0] . u N[%]](HTMLFiles/index_58.gif)
Out[260]=
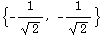
Out[261]=
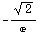
Out[262]=
![RowBox[{-, 0.52026}]](HTMLFiles/index_61.gif)
Exercise 1
Suppose there is a spaceship in three-dimensional space, with our sun located at the origin, (0,0,0). The temperature near the sun is extremely hot, of course -- about 6000K -- and it drops rapidly as one moves away. Suppose the temperate at any point is space is given by 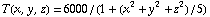 , where x, y, and z measured in units of 10 million miles. (Here we're assuming the spaceship will never get close enough to other stars to notice their heat, so effectively our sun is the only heat-producer in the universe.)
, where x, y, and z measured in units of 10 million miles. (Here we're assuming the spaceship will never get close enough to other stars to notice their heat, so effectively our sun is the only heat-producer in the universe.)
Suppose now that the spaceship is located on the Earth, about 93 million miles away, at the point (9,2,1). What is the directional derivative (change in K per change in position) if the spaceship were to move in the direction of the vector (-4,-3,5)?
(If you're interested in how to find the surface temperature of a star, look at
http://zebu.uoregon.edu/~soper/Stars/color.html., or any of the other pages you can find on Google by searching for "Star Temperature Color" or something similar.)
Exercise 2
Using the same setup as in Example 1, suppose the spaceship is situated at the point (4,-2,8). If the ship were to fly in the direction of the point (-4,3,7), would the initial change in temperature be an increase or a decrease?
Vector Fields
A Vector Field is one of the most fundamental concepts in Multivariable Calculus and Vector Analysis. One of the main reason this course exists is to teach you four specific theorems: the Fundamental Theorem of Line Integrals, Green's Theorem, Stokes' Theorem, and the Divergence Theorem. Every single one of these theorems involves vector fields! If you take a little time now to understand what a vector field is, you'll save yourself some time and grief later on.
In lecture you've already talked about linear transformations, so you should hopefully be comfortable with the idea of a function 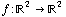 . This notation means that
. This notation means that 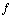 takes two inputs and has two outputs. You've also learned that a linear transformation with two inputs and outputs can be represented by a 2 by 2 matrix.
takes two inputs and has two outputs. You've also learned that a linear transformation with two inputs and outputs can be represented by a 2 by 2 matrix.
A (two-dimensional) vector field is simply a function 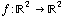 , but there are two key differences: (1)
, but there are two key differences: (1) 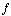 is not necessarily a linear function, so it might or might not be possible to represent it using a matrix, and (2) we interpret the inputs and outputs in a different way.
is not necessarily a linear function, so it might or might not be possible to represent it using a matrix, and (2) we interpret the inputs and outputs in a different way.
Graphing a Vector Field
Let's look at an example. Traditionally we represent vector fields with capital letters, so we'll call our first field 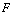 instead of
instead of 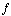 .
.
In[263]:=
![F[x_, y_] = {-y, x}](HTMLFiles/index_69.gif)
Out[263]=
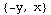
Here's the key to understanding vector fields: we think of the inputs as points, and the outputs as vectors. For example, 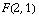 is the vector (-1,2):
is the vector (-1,2):
In[264]:=
![F[2, 1]](HTMLFiles/index_72.gif)
Out[264]=
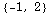
To draw a picture of the vector field, we simply draw the vector (-1,2) -- the output -- beginning at the point (2,1) -- the input. In other words, we draw a vector which goes from (2,1) to (1,3). (Check my arithmetic here!)
Here are a whole bunch of values of the vector field:
In[265]:=
![F[0, 0] F[1, 0] F[2, 0] F[0, 1] F[1, 1] F[2, 1] F[0, 2] F[1, 2] F[2, 2]](HTMLFiles/index_74.gif)
Out[265]=
Out[266]=
Out[267]=
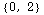
Out[268]=
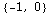
Out[269]=
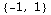
Out[270]=
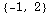
Out[271]=
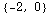
Out[272]=
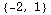
Out[273]=
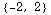
And here's a picture where we've drawn in each of these vectors, starting at their respective points. (You don't have to understand this command, although if you look at it long enough you can probably kind of figure out what's going on.)
In[274]:=
![Show[Graphics[{Arrow[{0, 0}, {0, 0}], Arrow[{1, 0}, {1, 1}], Arrow[{2, 0}, {2, 2}], Arrow[{0, ... Arrow[{1, 2}, {-1, 3}], Arrow[{2, 2}, {0, 4}]}], AxesTrue, AspectRatioAutomatic] ;](HTMLFiles/index_84.gif)
![[Graphics:HTMLFiles/index_85.gif]](HTMLFiles/index_85.gif)
While that's somewhat interesting, it's awfully tedious, and it would take forever to tell what the "big picture" is. Fortunately Mathematica includes a command to graph vector fields for you. Here's a picture of 
In[275]:=
![PlotVectorField[{-y, x}, {x, -5, 5}, {y, -5, 5}, AxesTrue]](HTMLFiles/index_87.gif)
![[Graphics:HTMLFiles/index_88.gif]](HTMLFiles/index_88.gif)
Out[275]=
Wow! Imagine having to draw each of those arrows by hand. This is definitely a case where a computer can make your life easier, BUT... you need to be careful, because Mathematica is hiding some of the details from you. Look above at the picture we constructed "manually." At the point (1,1) you can see the vector (-1,1), which has length 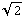 . But if you look at the computer generated picture, the vector starting at (1,1) is so short that you can only see the arrow head! Mathematica is scaling the vectors, trying to make the picture easier to look at; while that's a noble goal, it means you do lose some information -- namely, exactly how long those vectors are.
. But if you look at the computer generated picture, the vector starting at (1,1) is so short that you can only see the arrow head! Mathematica is scaling the vectors, trying to make the picture easier to look at; while that's a noble goal, it means you do lose some information -- namely, exactly how long those vectors are.
Evaluate the next cell to show the vectors at full length. We' added the ScaleFactor->None option to turn off the scaling.
In[276]:=
![PlotVectorField[{-y, x}, {x, -5, 5}, {y, -5, 5}, ScaleFactorNone, AxesTrue]](HTMLFiles/index_91.gif)
![[Graphics:HTMLFiles/index_92.gif]](HTMLFiles/index_92.gif)
Out[276]=
That's a much different picture! So now you can see that Mathematica was really distorting your view of what's going on. However, you can also see what the designers of Mathematica were thinking; if you show the whole vectors, it can get very crowded. You can use the ScaleFactor option to fiddle around with a picture to suit your own tastes. You've already seen what setting this option to None can do; if you set it to a number instead, then Mathematica will rescale the longest vector in the picture to have that length. For this particular vector field (with this range of x and y) it seems like scaling the vectors to have length 2 or less is a nice compromise.
In[277]:=
![PlotVectorField[{-y, x}, {x, -5, 5}, {y, -5, 5}, ScaleFactor2, AxesTrue]](HTMLFiles/index_94.gif)
![[Graphics:HTMLFiles/index_95.gif]](HTMLFiles/index_95.gif)
Out[277]=
Why Vector Fields are Useful
The last picture looks like it represents some sort of circular motion, and that's a clue about why vector fields are important. Very often we'll think of vector fields as representing fluid flow, in which case this vector field would represent some kind of whirlpool or drain.
Sometimes we'll also think of a vector field as a force field; in other words, each vector represents some kind of force, whether from an explosion, or gravity, etc.
Here are a few examples of vector fields for you took look at. Look at the functions and try to understand why the picture looks the way it does. Also play around with the ScaleFactor option to see how it affects the pictures. Which works better, the Automatic or None setting?
The "Blowup" or "Super Nova" Vector Field
In[278]:=
![F[x_, y_] = {x, y} PlotVectorField[F[x, y], {x, -5, 5}, {y, -5, 5}, ScaleFactorAutomatic, AxesTrue]](HTMLFiles/index_97.gif)
Out[278]=
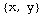
![[Graphics:HTMLFiles/index_99.gif]](HTMLFiles/index_99.gif)
Out[279]=
The "Black Hole" Vector Field
Can you explain what happens when you set ScaleFactor to None here?
In[280]:=
![F[x_, y_] = {-x, -y} PlotVectorField[F[x, y], {x, -5, 5}, {y, -5, 5}, ScaleFactorAutomatic, AxesTrue]](HTMLFiles/index_101.gif)
Out[280]=
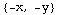
![[Graphics:HTMLFiles/index_103.gif]](HTMLFiles/index_103.gif)
Out[281]=
The "Important" Vector Field
This vector field looks a lot like the very first example we worked with. See if you can tell how it's different. This particular vector field has some very unique characteristics, which you'll learn about in lecture. That's why we called it "important" here; it also has a tendency to show up in textbooks and on exams.
In[282]:=
![F[x_, y_] = {-y/(x^2 + y^2), x/(x^2 + y^2)} PlotVectorField[F[x, y], {x, -5, 5}, {y, -5, 5}, ScaleFactorAutomatic, AxesTrue, PlotPoints16]](HTMLFiles/index_105.gif)
Out[282]=
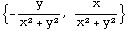
![[Graphics:HTMLFiles/index_107.gif]](HTMLFiles/index_107.gif)
Out[283]=
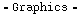
The "Curving River"
In[284]:=
![F[x_, y_] = {1, Sin[x]} PlotVectorField[F[x, y], {x, -Pi/2, Pi/2}, {y, -Pi/2, Pi/2}, AxesTrue]](HTMLFiles/index_109.gif)
Out[284]=
![{1, Sin[x]}](HTMLFiles/index_110.gif)
![[Graphics:HTMLFiles/index_111.gif]](HTMLFiles/index_111.gif)
Out[285]=
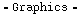
Vector Fields in 3D
Many -- maybe most -- of the vector fields you'll work with this semester are three-dimensional. That means we have a function 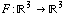 instead of
instead of 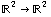 . Everything else you've learned goes the same way: the three inputs are the (x,y,z) coordinates of a point, and the output is a three dimensional vector which you draw beginning at the input point (x,y,z).
. Everything else you've learned goes the same way: the three inputs are the (x,y,z) coordinates of a point, and the output is a three dimensional vector which you draw beginning at the input point (x,y,z).
Mathematica can draw 3D vector fields, but you'll quickly see why we tend to concentrate on 2D examples when we're talking about these ideas. It just gets too messy when you look at a three dimensional picture. Look at this example of a 3D vector field, which is almost the same as the first 2D vector field we considered above:
In[286]:=
![F[x_, y_, z_] = {-y, x, z} PlotVectorField3D[F[x, y, z], {x, -5, 5}, {y, -5, 5}, {z, -5, 5}, AxesTrue]](HTMLFiles/index_115.gif)
Out[286]=
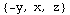
![[Graphics:HTMLFiles/index_117.gif]](HTMLFiles/index_117.gif)
Out[287]=
Mathematica is trying valiantly to keep things from getting too messy. It's scaling the vectors, as before, and it's also removed the arrows at the end of the vectors. While the missing arrows make things a little less cluttered, it's a big loss of information because you have no way of knowing which directions things are heading in.
If you'd like to put the arrows back in, you can use the VectorHeads option. We've done that in the next command here, along with turning the scaling off.
In[288]:=
![F[x_, y_, z_] = {-y, x, z} PlotVectorField3D[F[x, y, z], {x, -5, 5}, {y, -5, 5}, {z, -5, 5}, AxesTrue, VectorHeadsTrue, ScaleFactorNone]](HTMLFiles/index_119.gif)
Out[288]=
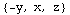
![[Graphics:HTMLFiles/index_121.gif]](HTMLFiles/index_121.gif)
Out[289]=
Now you can see why, although we work with 3D vector fields all the time, we very rarely draw pictures of them!
Gravity
One 3D vector field that can be drawn fairly easily is the gravitational force field on the surface of the earth. Of course, the only reason we can draw it is because it's such a simple force field. Look at the function and see if you can guess what the picture will look like before evaluating the cell.
In[290]:=
![RowBox[{F[x_, y_, z_], =, RowBox[{{, RowBox[{0, ,, 0, ,, RowBox[{-, 9.8}]}], }}]}] PlotVectorF ... 0, 50}, VectorHeadsTrue, AxesTrue, ScaleFactorFalse, PlotPoints5]](HTMLFiles/index_123.gif)
Out[290]=
![RowBox[{{, RowBox[{0, ,, 0, ,, RowBox[{-, 9.8}]}], }}]](HTMLFiles/index_124.gif)
![[Graphics:HTMLFiles/index_125.gif]](HTMLFiles/index_125.gif)
Out[291]=
The Gradient Revisited; Tying it all Together
Now let's combine the two previous sections. If we have a function 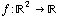 , we can take its gradient, which is a function
, we can take its gradient, which is a function 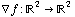 . Read that again -- it's tricky. f takes two inputs, and its gradient takes the same two inputs, and gives you two outputs back -- namely, the two partial derivatives.
. Read that again -- it's tricky. f takes two inputs, and its gradient takes the same two inputs, and gives you two outputs back -- namely, the two partial derivatives.
But wait! If the gradient is a function 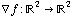 , then we can think of the gradient of a function as a vector field! And thus the idea of a "gradient vector field" is born. You'll run across that term fairly often. It just means a vector field which happens to be the gradient of some (possibly unknown!) function.
, then we can think of the gradient of a function as a vector field! And thus the idea of a "gradient vector field" is born. You'll run across that term fairly often. It just means a vector field which happens to be the gradient of some (possibly unknown!) function.
In[292]:=
![f[x_, y_] = x * y gradf[x_, y_] = Grad2D[f[x, y]] gradfieldpic = PlotVectorField[gradf[x, y], {x, -5, 5}, {y, -5, 5}, AxesTrue]](HTMLFiles/index_130.gif)
Out[292]=
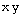
Out[293]=
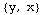
![[Graphics:HTMLFiles/index_133.gif]](HTMLFiles/index_133.gif)
Out[294]=
Gradient vector fields are important because they have a property called "path independence," which you'll learn about later in this course. For today we'll concentrate on a different idea, the fact that gradients are perpendicular (or "orthogonal," or "normal," all of which mean the same thing) to level sets of a function. This will help us tie a few loose ends with the directional derivative, too.
Remember that, for a function 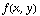 , a level set is the set of all points (x,y) such that
, a level set is the set of all points (x,y) such that 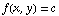 , where c is some constant number you've already chosen. For example, with our function
, where c is some constant number you've already chosen. For example, with our function 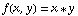 that we just used,
that we just used,
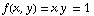 is the same as y=1/x, which is a hyperbola,
is the same as y=1/x, which is a hyperbola,
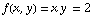 is the same as y=2/x, which is a hyperbola,
is the same as y=2/x, which is a hyperbola,
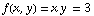 is the same as y=3/x, which is a hyperbola,
is the same as y=3/x, which is a hyperbola,
and so on. Essentially we're finding all of the points where the height of the surface 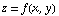 is equal to 1 (or 2, or 3). We could plot these together:
is equal to 1 (or 2, or 3). We could plot these together:
In[295]:=
![Plot[{1/x, 2/x, 3/x}, {x, -5, 5}, PlotRange {-5, 5}, AspectRatioAutomatic]](HTMLFiles/index_142.gif)
![[Graphics:HTMLFiles/index_143.gif]](HTMLFiles/index_143.gif)
Out[295]=
But wait! If we're looking for points where the height has a certain values, then we're really looking for contour lines. Remember ContourPlot? It can generate a nice picture of this function. (Go look at Lab 1B if you don't remember this command.) It shows us the various "elevation lines" of the graph, including those for negative elevation.
In[296]:=
![contourpic = ContourPlot[f[x, y], {x, -5, 5}, {y, -5, 5}]](HTMLFiles/index_145.gif)
![[Graphics:HTMLFiles/index_146.gif]](HTMLFiles/index_146.gif)
Out[296]=
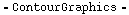
Now let's look at the contour plot and the gradient field together. There's an extra option here to make the arrows blue in the picture of the vector field; you don't need to worry about figuring that out. Also, the DisplayFunction stuff prevents Mathematica from drawing a picture of the vector field until we show both pictures together.
In[297]:=
![gradfieldpic = PlotVectorField[gradf[x, y], {x, -4, 4}, {y, -4, 4}, AxesTrue, ColorFun ... tionIdentity] ; Show[contourpic, gradfieldpic, DisplayFunction$DisplayFunction] ;](HTMLFiles/index_148.gif)
![[Graphics:HTMLFiles/index_149.gif]](HTMLFiles/index_149.gif)
Notice that the blue vectors in the picture are perpendicular to the level curves (i.e. the contour lines). This is no accident! In fact, it's always true that
If the point (x,y) is on the level curve 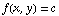 , then
, then 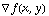 will be perpendicular to the level curve.
will be perpendicular to the level curve.
(More technically, if you draw the tangent line which touches the curve at the point (x,y), then the gradient vector at that point will be perpendicular to the tangent line.)
The same is true in any dimension. If you have a function 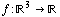 , then the level sets will be level surfaces, and the gradient will be perpendicular to the level surfaces. (That is, if
, then the level sets will be level surfaces, and the gradient will be perpendicular to the level surfaces. (That is, if 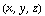 is on some level surface, then the gradient
is on some level surface, then the gradient 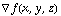 will be perpendicular -- or "normal" -- to the tangent plane which touches the surface at (x,y,z).
will be perpendicular -- or "normal" -- to the tangent plane which touches the surface at (x,y,z).
You won't be asked to use this fact about gradients and level sets for the rest of this lab, but it will be very important in next week's lab.
There's a little more to be said about the picture above. Remember that ContourPlot shades the low areas with dark colors, and the high areas with bright colors. Notice how the gradient vectors always seem to point straight uphill. Once again, that's no accident. Remember,
![D_Overscript[u, ⇀] f(a) = Overscript[∇, ⇀] f(a) · Overscript[u, ⇀],](HTMLFiles/index_155.gif)
and if we combine that with the definition of a dot product, along with the fact that ![Overscript[u, ⇀]](HTMLFiles/index_156.gif) is a unit vector (and therefore has length one):
is a unit vector (and therefore has length one):
![D_Overscript[u, ⇀] f(a) = Overscript[∇, ⇀] f(a) · Overscript[u, ⇀] = | ... || || Overscript[u, ⇀] || cos(θ) = || Overscript[∇, ⇀] f(a) || cos(θ)](HTMLFiles/index_157.gif)
where θ is the angle between the gradient vector and the vector ![Overscript[u, ⇀]](HTMLFiles/index_158.gif) , i.e. the angle between the gradient and the direction that we're going. The largest this can be is when cos(θ)=1, which happens for θ=0. In other words,
, i.e. the angle between the gradient and the direction that we're going. The largest this can be is when cos(θ)=1, which happens for θ=0. In other words,
"The largest the directional derivative can be is when the angle between the gradient and our direction is 0 -- in other words, when we're looking in the direction of the gradient vector."
Rephrased one more time:
The largest value of the directional derivative is in the direction of the gradient; equivalently, the gradient points in the direction of the largest increase.
Exercise 3
Recall the setup for Exercises 1 and 2:
Suppose there is a spaceship in three-dimensional space, with our sun located at the origin, (0,0,0). The temperature near the sun is extremely hot, of course -- about 6000K -- and it drops rapidly as one moves away. Suppose the temperate at any point is space is given by 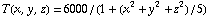 , where x, y, and z measured in units of 10 million miles. (Here we're assuming the spaceship will never get close enough to other stars to notice their heat, so effectively our sun is the only heat-producer in the universe.)
, where x, y, and z measured in units of 10 million miles. (Here we're assuming the spaceship will never get close enough to other stars to notice their heat, so effectively our sun is the only heat-producer in the universe.)
Let's assume again that the spaceship is located on the Earth, about 93 million miles away, at the point (9,2,1). In what direction is the largest increase in temperature? Why is this not the least bit surprising? In which direction could the spaceship go to remain at the same temperature? (This is much harder than the first question in this paragraph.)
(If you're assigned this problem, it's not worthy of a separate writeup. You should include your answer as an "interesting aside" in your answer to Exercise 1.)
Exercise 4
Assuming the spaceship is at the point (4,-2,8). In which direction should the spacecraft move in order to decrease the temperature as quickly as possible. What direction could the spacecraft go to keep the temperature constant?
If you're assigned this problem, you should include your answers as part of your writeup to Exercise 2, instead of doing a separate problem.
Credits
Created by
Mathematica
(November 6, 2004)
![[Graphics:HTMLFiles/index_5.gif]](HTMLFiles/index_5.gif)
![gradf[x_, y_] = Grad2D[f[x, y]] gradf[1, 0] u gradf[1, 0] . u](HTMLFiles/index_49.gif)
![F[0, 0] F[1, 0] F[2, 0] F[0, 1] F[1, 1] F[2, 1] F[0, 2] F[1, 2] F[2, 2]](HTMLFiles/index_74.gif)
![Show[Graphics[{Arrow[{0, 0}, {0, 0}], Arrow[{1, 0}, {1, 1}], Arrow[{2, 0}, {2, 2}], Arrow[{0, ... Arrow[{1, 2}, {-1, 3}], Arrow[{2, 2}, {0, 4}]}], AxesTrue, AspectRatioAutomatic] ;](HTMLFiles/index_84.gif)
![[Graphics:HTMLFiles/index_85.gif]](HTMLFiles/index_85.gif)
![[Graphics:HTMLFiles/index_88.gif]](HTMLFiles/index_88.gif)
![[Graphics:HTMLFiles/index_92.gif]](HTMLFiles/index_92.gif)
![[Graphics:HTMLFiles/index_95.gif]](HTMLFiles/index_95.gif)
![[Graphics:HTMLFiles/index_99.gif]](HTMLFiles/index_99.gif)
![[Graphics:HTMLFiles/index_103.gif]](HTMLFiles/index_103.gif)
![[Graphics:HTMLFiles/index_107.gif]](HTMLFiles/index_107.gif)
![[Graphics:HTMLFiles/index_111.gif]](HTMLFiles/index_111.gif)
![[Graphics:HTMLFiles/index_117.gif]](HTMLFiles/index_117.gif)
![[Graphics:HTMLFiles/index_121.gif]](HTMLFiles/index_121.gif)
![RowBox[{F[x_, y_, z_], =, RowBox[{{, RowBox[{0, ,, 0, ,, RowBox[{-, 9.8}]}], }}]}] PlotVectorF ... 0, 50}, VectorHeadsTrue, AxesTrue, ScaleFactorFalse, PlotPoints5]](HTMLFiles/index_123.gif)
![[Graphics:HTMLFiles/index_125.gif]](HTMLFiles/index_125.gif)
![f[x_, y_] = x * y gradf[x_, y_] = Grad2D[f[x, y]] gradfieldpic = PlotVectorField[gradf[x, y], {x, -5, 5}, {y, -5, 5}, AxesTrue]](HTMLFiles/index_130.gif)
![[Graphics:HTMLFiles/index_133.gif]](HTMLFiles/index_133.gif)
![[Graphics:HTMLFiles/index_143.gif]](HTMLFiles/index_143.gif)
![[Graphics:HTMLFiles/index_146.gif]](HTMLFiles/index_146.gif)
![gradfieldpic = PlotVectorField[gradf[x, y], {x, -4, 4}, {y, -4, 4}, AxesTrue, ColorFun ... tionIdentity] ; Show[contourpic, gradfieldpic, DisplayFunction$DisplayFunction] ;](HTMLFiles/index_148.gif)
![[Graphics:HTMLFiles/index_149.gif]](HTMLFiles/index_149.gif)
![D_Overscript[u, ⇀] f(a) = Overscript[∇, ⇀] f(a) · Overscript[u, ⇀] = | ... || || Overscript[u, ⇀] || cos(θ) = || Overscript[∇, ⇀] f(a) || cos(θ)](HTMLFiles/index_157.gif)