Lab 6A - Surface Integrals of Scalar Functions
Math 2374 - University of Minnesota
http://www.math.umn.edu/math2374
questions to: rogness@math.umn.edu

Introduction

All semester long we've been taking the concepts you learned during the first year of calculus and generalizing them to higher dimensions.  For example,

• Instead of one derivative, now we have many different partial derivatives, one for each variable in the function.  (We also have a "total derivative," or "derivative matrix," which is a matrix made up of all the partial derivatives.)

• A single definite integral, such as 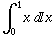, could be thought of as an integral along the line segment on the x-axis where x ranges from 0 to 1.  We've generalized this idea to come up with line or path integrals, where we integrate over a curve in space instead of a line segment on the x-axis.

• We also have iterated integrals, which allow us to compute double and triple integrals.  Double integrals let us integrate a function over a region R in the xy-plane.

Over the next two weeks in lab, we're going to generalize this last idea.  Instead of integrating over a region R in the xy-plane, we're going to integrate over a two-dimensional region which is sitting in space, i.e. a surface.  This week we'll work with integrals of scalar functions on a surface; next week we'll integrate vector fields on a surface.

The concepts in this lab can be difficult to understand, so it's very important that you read through this whole lab; we'll try to give you lots of hints along the way, but they won't be very helpful hints if you miss them!  Half of the work in any of these problems is finding a parametrization for a surface, and many people have trouble with this part.  We've tried to make it easier on you by getting you started on parametrizing surfaces way back in Lab 2B.  You might find it useful to open Lab 2B in another window so you can refer back to it.

One reminder before we move on.  Many of the formulas involve the length (or norm) of a vector, i.e. .  You might recall from an earlier lab that we can compute this in Mathematica using the Norm function.  Evaluate the next two cells before moving on and make sure the output is what you would expect.

In[546]:=

Out[546]=

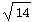
In[547]:=

Out[547]=

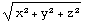
Mathematica has a built-in function called Norm, but it assumes that it's working with complex numbers (things like 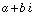), so it doesn't work quite right for us.  Instead Norm is redefined in math2374.nb like this:



(Here v is a vector.)  Why is this the correct definition?  Talk to your TA if you're not sure.

We're also going to use the command Cross to find the cross product of two vectors.  If you aren't sure how to use this command, look it up in the help browser.

Definition

Just for your reference, we'll repeat the definition of a surface integral of a scalar function.

Let 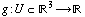be a continuous function, and let M be a smooth surface lying in U that is parametrized by f(s,t), where 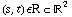.  The surface integral of g over M is:

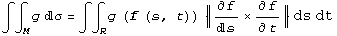
Example

(This is based on similar examples in most textbooks.  Here we'll concentrate on the concepts and let Mathematica do all the hard work.)

Evaluate the surface integral of 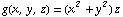over the upper half of the sphere of radius 1 centered at the origin.

The first step in any surface integral is generally to find a parametrization for the surface.  In this case we need to parametrize the upper half of the unit sphere.  There are a few ways to do this, but because this is a sphere, it's probably best to use spherical coordinates.

Recall from Lab 2B that one of the best ways to parametrize a surface is often to describe it in cylindrical or spherical coordinates, and then convert the description back into rectangular coordinates.  (Remember, our final parametrization has to be in rectangular coordinates!)  In this particular case, the description of the upper half of the sphere is simply ρ=1, where 0≤θ≤2π and 0≤φ≤π/2.  (If this doesn't make sense, you should open your textbook and re-read the section on spherical coordinates.)

So ρ is constant, and the angles θ and φ will be our parameters.  Using the change of coordinate formulas, we get the following parametrization (with the same bounds on θ and φ as before):

In[548]:=

Out[549]=

Now we're asked to integrate the function 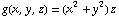over the sphere.  Sometimes people have a hard time visualizing what this actually means.  Suppose our hemisphere is made up of a mixture of different kinds of metals, and different parts of the sphere have a different density, represented by the function g.  Here's a different graph of our surface, where the hemisphere is colored according to the function g; lighter shades indicate larger values of g, while dark areas on the sphere represent areas where the value of g is lower.  

FYI: You do not have to understand the following commands; just evaluate them to see the picture!  If you'd rather have a plain old graph instead of an interactive picture, change ParametricPlot3DLive to ParametricPlot3D.  I used a Live command here because we're going to refer to the picture again in a few minutes, so you can keep it off to the side in the Live window.

In[550]:=

Out[552]=

So, for example, if g represents the density of the material making up the hemisphere, the lighter areas are constructed of much denser material than the darker areas.  The integral of g over the surface will give us the total mass of the hemisphere.

The first step to compute the integral, as you can see by looking at the definition above or in your book, is to find the partial derivatives of our parametrization f(θ,φ).  To save some typing and reading time, let's simply write "t" and "p" instead of "theta" and "phi" for our variable names.

In[553]:=

Out[553]=

Out[554]=

Now we have to cross the partials and find the length of the resulting cross product.  Remember that we've defined a function Norm to do this for us.

In[555]:=

Out[556]=

This looks truly horrendous, but if you use Simplify you'll see that it's actually much better.

The other piece of our integrand is g(f(θ,φ)).  Recall from Lab 4A that the correct way to do this in Mathematica is to use the Apply command.  If you don't remember this, go look at Lab 4A again.

In[557]:=

Out[558]=

Again, this can be simplified if you like.

Now that you've seen how we can compute each piece of the integrand separately, we can do it all at once.  (If we had simply used this command right away it probably would have confused everybody)

In[559]:=

Out[559]=

Out[560]=

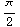
So if g represents the density of the material of the hemisphere, the total mass of the hemisphere is .

Careful: we're being a bit sloppy here.  If we were actually working with densities and mass, we really ought to include units!  In fact, it's even worse; we usually think of our surfaces as being two-dimensional, whereas you might only think a three-dimensional object could have any mass.  If you prefer, you could imagine the surface as a very, very thin piece of paper or rubber.

Here's an interesting little afterthought.  If you look at the earlier picture which is shaded in black and white according to g, you can see that the larger values of g are concentrated in the middle of the hemisphere.  Close to the north pole, the shading is much darker, which means the values of g are much smaller.  If g is a density function, that means there's not much mass in this part of the hemisphere.  To verify this with integrals, you can evaluate the following commands.  These are the same integrals as before, with one difference; instead of doing the whole hemisphere at once, the first integral is restricted to the area near the north pole (φ goes to π/6 instead of π/2=3π/6), the second integral does the "middle" of the hemisphere (π/6≤φ≤2π/6), and the third does the section near the equator (2π/6≤φ≤3π/6).

In[561]:=

Out[561]=

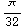
Out[562]=

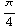
Out[563]=

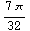
You might remember that average density is equal to mass divided by surface area.  We can find surface area of these pieces by integrating the function 1 over the surface.  Remember that if we're integrating 1, then the integrand is actually 1 times the length of the normal vector:

In[564]:=

Out[564]=

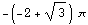
Out[565]=

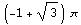
Out[566]=

In[567]:=

Out[567]=

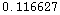
Out[568]=

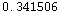
Out[569]=

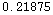
So you can see that the density really is concentrated in the middle of the sphere, with somewhat less along the equator, and significantly less near the north pole!

Donuts and Chocolate Frosting

Now we come to the important, real world application: measuring chocolate.

In the homework you may have been asked to parametrize a "torus," which is the mathematical term for the surface of a donut shape.  This is a very famous and widely used surface in mathematica.  Mathematica even includes commands for drawing tori (not toruses!).  Note that you don't have to understand these commands, but you can evaluate them if you'd like to see a picture.

In[570]:=

Out[570]=

In case you didn't manage to do the homework problem in question, here's the parametrization for a certain torus.  If you graph this parametrization with both θ and φ going from 0 to 2π, you'll see the whole torus.  (Try it if you'd like to.)  Note that I'm typing "t" and "p" instead of "theta" and "phi," or "θ" and "φ."

In[571]:=

Here's the setup for our example.  Suppose we bake a donut, and then we dip it upside down in a vat of dark chocolate, so we coat the upper half of the donut with gooey chocolate frosting.  The chocolate in the vat isn't perfectly mixed, so the denser chocolate is settling at the bottom of the vat.  What that means is that the chocolate which ends up on the top of the donut -- remember, it's dipped upside down -- is denser than the chocolate on the sides.  We want to know how much chocolate is actually there.  We're going to do that by estimating the density of the chocolate coating at each point on the top half of the donut, and then integrating the density function over this half.

The way we've chosen the parametrization, the chocolate is on the top half of the torus, which just happens to be precisely those points on or above the xy-plane, where z=0.  Evaluate the next two commands to see pictures of the surface we're going to integrate over.  We use the same parametrization, but now 0≤φ≤2π and -π/2≤θ≤π/2.

In[572]:=

In[573]:=

Out[573]=

Alternatively, you could evaluate the next command to show the surface in a LiveGraphics3D window:

In[574]:=

Suppose the density function is 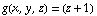.  A graph of the chocolate surface looks like this:

In[575]:=

Out[576]=

(Again, you do not need to understand these commands; they're just here so that you can see a picture which illustrates our situation.)

Unlike in the previous example, the darker shades here represent the denser chocolate (because our chocolate is dark, after all).  Now that we've seen all of the pretty pictures, we're ready to calculate the mass of the chocolate by integrating g over the top half of the torus.  I'm not going to explain the commands much, so if you don't understand what's going on, scroll back up and look at the first example again.  I will make a few comments; they are in between the (* and *) symbols.

In[577]:=

Out[582]=

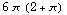
Out[583]=

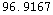
There are semicolons after most of these commands, so the only outputs are the final answer, in simplified form, and a numerical approximation.  If you'd like to see the partials, or the integrand, you can remove the appropriate semicolons and evaluate the cell again.

So with our given setup, there are almost 97 grams of chocolate on this surface.  (Sounds like a good donut!)

Exercises

Note: in the examples above, you were shown graphs which were colored according to the scalar function g(x,y,z), instead of Mathematica's normal internal coloring scheme.  You do not have to produce these kinds of graphs in your lab report!

Exercise 1

Find the surface area of the surface parametrized (and graphed) by the following commands.  (You will need to cut and paste before you can evaluate them.)



Your answer should include a sketch of the surface, your exact answer -- which will be ugly -- and a numeric approximation, which you can find using the N command in Mathematica.  Alternatively, you could use the command NIntegrate to get your numeric approximation.  NIntegrate will not try to give you an exact answer, but will only give you the approximation.

Exercise 2

Find the surface area of the surface parametrized (and graphed) by the following commands.  (You will need to cut and paste before you can evaluate them.)



Your answer should include a sketch of the surface, and a numeric approximation to the final answer.  You'll have to use NIntegrate instead of Integrate (see exercise 1).  Integrate will think for a long, long time and probably not give you an answer.

Exercise 3

Evaluate the surface integral of the function 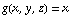over the surface which is the graph of , where 0≤x≤2π and -π≤y≤π.  Note that you will have to use NIntegrate with this exercise; once again Integrate can't quite get the answer, although it gives it a good try.

Exercise 4

Evaluate the surface integral of the function 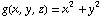over the following surface:



You should include a picture of the surface along with your work.  As with exercises 2 and 3, you'll have to use NIntegrate here.

Created by Mathematica  (November 6, 2004)