Change of Variables: Polar to Rectangular Coordinates

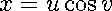
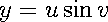
In multivariable calculus, we often use a "change of variables" transformation to make our double integrals easier to evaluate. One of the most commonly used transformations is given by

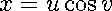
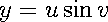
Of course, this is nothing more than the usual transformation from polar coordinates to rectangular coordinates, where u is taking the place of the radius r, and v is the angle θ.

The following picture shows this transformation applied to the rectangle

in uv-space. The image of R is shown on the right. You can also see the image of a small subrectangle of R. Click on the red rectangle in uv-space and move it to see what happens to its image in xy-space.

Here's a question for you to think about. The Area Expansion Factor (i.e. the determinent of the Jacobian) for this transformation is simply u. As you move the red rectangle around, can you see geometrically why this is true?