Assignment 8 - Due Thursday 10/30/2003
Read: Hubbard and Hubbard Section 1.9. I hope to start on 2.1 during the week.
Exercises:
Hand in only the exercises which have stars by them.
Section 1.9 (page 162): 3*
Section 1.10 (pages 162-168): 26b, 27, 28*, 29*, 30, 31
Extra Questions:
1. Given that
find the derivative matrix of the composite function 
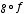at (x,y) = (1,1); also at (x,y) = (0,0).2. Consider the curve defined parametrically by
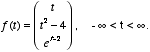Let g(x,y,z) be a real-valued differentiable function of three variables. If a = (2,0,1) and
find
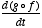at t = 2.3*. Let
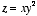and suppose that x = 2u + 3v. Assume also that y is a function of u and v with the properties that when (u,v) = (2,1) then 
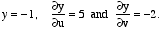Find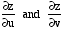 
when (u,v) = (2,1).4*. Show that for a differentiable real-valued function g(x,y),
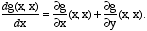
Apply this equation to the function
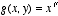. [Hint: Consider the composite of g with the function f(x) = (x,x).]Peter's Paragraph:
We have already seen the type of example presented in Section 1.9, and we do not need to dwell on these things much longer. The main result in this section, Theorem 1.9.7, is important to know, but I do not think we need trouble ourselves much with the proof. Having done derivatives in a fancy way with slick notation, it is important also to recognize the formulation of these things using partial derivatives, because that is probably what you will encounter in physics. Some of the extra questions are supposed to be practice for this.