Assignment 4 - Due Thursday 2/19/2004
The first mid-term exam will be held on 1/19 in recitation. There will be no quiz. The questions on the exam will be about Sections 3.1 - 3.7 of the book. You may use a calculator. You may not use notes, the book or a computer.
Read: Hubbard and Hubbard Sections 3.7. We may also start on Section 4.1, but I set no homework questions on this section.
Exercises:
Section 3.7 (pages 375-377): 1, 2, 3*, 4*, 5, 6, 7, 8*, 9, 10a*, 10b*, 11, 13, 14.
Hint for 10: let v be an eigenvector and see what you can say about
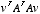.Extra question: A* Let
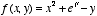be defined only on the unit disc 
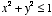. Show that on the unit disc this function takes its maximum value on the boundary. Calculate the maximum value and a point at which it takes it.Hint: The equation
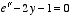has two roots, the larger of which is greater than 1. At the end of this question use a calculator.Peter's Paragraphs
I have failed again to cover the material specified in the last assignment done in a reasonable time, and at Oleg's excellent suggestion the questions from Section 3.7 which were due last week are in fact due this week. Also the pages about the spectral theorem at the end of Section 3.7 are something which we will do this week. The proof that they offer of this theorem is one which uses Lagrange multipliers, and it is not the standard proof. I personally prefer the standard proof, but still this one is not so bad, so we will study it. The unfortunate thing about it is that they do not tell you at all how to find eigenvalues of a matrix (and then eigenvectors): they are the roots of the characteristic polynomial. Perhaps you know this already?
I have spent quite some time trying to decide what to do about Section 3.8, which is about curvature. They get into some quite complicated formulas for computing curvature, and I do not think it helps one's understanding of curvature particularly to be fluent with this formulas. I would prefer a more rudimentary presentation with just the key facts. As it is, I think we should skip this section. This is a pity since only a few months ago it was determined with some accuracy that the universe we live in is flat, and not curved. It is nice to have some conception of what this means. If we have time at the end of the course (which, probably, we will not) we could come back to this.
Julian's Joke
What's the difference between roast beef and pea soup?
The difference is that everyone can roast beef.