Assignment 5 - Due Thursday 10/9/2008
Read: Hubbard and Hubbard Section 1.6.
Exercises:
Hand in only the exercises which have stars by them.
Section 0.7 (page 31): 4, 9, 12(ii)*, 13, 14.
Section 1.6 (pages 119-120): 1, 2*, 3*, 4*, 5, 6, 7
Extra questions:
1. Which of the following sequences of complex numbers tend to a limit? Justify your answer.
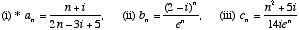
2. Which of the following series of complex numbers converge? Justify your answer.
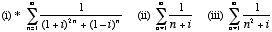
Comments:
The first mid-term exam will be held in the recitation on Thursday October 2. The material which will appear on the exam will be taken from sections 1.1 - 1.5 (up to page 88 only, open and closed sets), together with material such as has appeared in the extra questions I have written out on the assignment sheets. You may not use any book or notes. You may use a calculator, but not a computer.
There are 5 questions on the exam, but they have multiple parts, so that on average each part is worth about 7% of the total. The exam is officially 50 minutes, but it is my hope that Dan may allow you to stay in the room 5 or 10 minutes longer at the end, if you need it.
Some of the questions are routine calculation, of a kind we have practiced, so that if you are up to speed with what we have done you should be able to do those questions without really thinking. There are some other questions where you will have to think in a more individual manner. If you find yourself getting stuck on a question, do move on to another one. I think you should be able to do each question part in about 3 minutes or less, so if you are taking, say, 6 minutes on a part of a question, consider moving on.
If there is something on the exam, like a piece of notation, which you do not understand, do ask Nick. The worst he can do is to refuse to answer you, and it may save you some trouble.
If you find yourself needing more space to answer a question than is given to you the way the exam is printed, continue your answer on the reverse side of the paper, which will not have printing on it.
With the homework questions this week, one of the things we do in Section 1.6 is learn about the fundamental theorem of algebra, which is about complex numbers, so I have put in some questions about complex numbers to make sure that we can all do them. The extra questions have to do with limits, and these are defined for the complex numbers by regarding them as a copy of 2-dimensional space over the real numbers.