1. Competition/download webpage
2. Dataset description
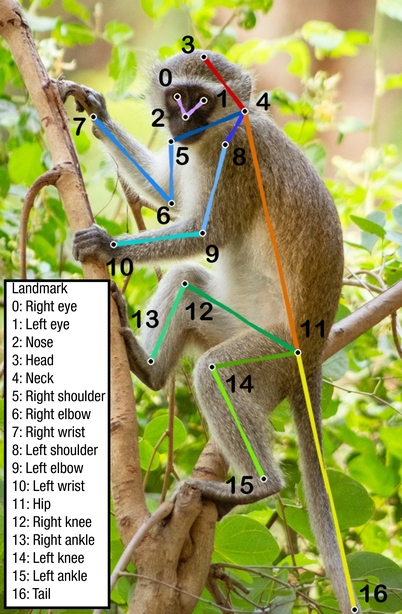
We collected 112,360 images of 26 species of primates (6 New World monkeys, 14 Old World monkeys, and 6 apes), including Japanese macaques, chimpanzees, and gorillas from (1) the internet images and videos, such as Flickr and YouTube, (2) photographs of multiple species of primates from three National Primate Research Centers, and (3) multiview videos of 27 Japanese macaques in the Minnesota Zoo. For each photograph, we cropped the region of interest such that each cropped image contains at least one primate. The 17 landmarks together comprise a pose. Our landmarks include Nose, Left eye, Right eye, Head, Neck, Left shoulder, Left elbow, Left wrist, Right shoulder, Right elbow, Right wrist, Hip, Left knee, Left ankle, Right knee, Right ankle, and Tail.
3. Data format
Each data instance is made of a triplet, {image, species, pose}. We use the following JSON format:annotation{
"image_id" : int,
"species_id" : int,
"file_name" : str,
"landmarks" : [x1,y1,v1, ...],
}
The testing result should be submitted in the following format:
annotation{
"image_id" : int,
"file_name" : str,
"landmarks" : [x1,y1, ...],
}
4. Evaluation

We evaluate the performance of pose detection using three standard metrics.
Mean per joint position error (MPJPE) [1] measures normalized error between the detection and ground truth for each landmark (the smaller, the better):
\[{\rm MPJPE}_i = \frac{1}{J}\sum_{j=1}^J \frac{\|\widehat{\mathbf{x}}_{ij} - \mathbf{x}_{ij}\|}{W}\]
where MPJPE\(_i\) is the MPJPE for the \(i^{\rm th}\) landmark, \(J\) is the number of image instances, \(\widehat{\mathbf{x}}_{ij}\in \mathbb{R}^2\) is the \(i^{\rm th}\) predicted landmark in the \(j^{\rm th}\) image, \(\mathbf{x}_{ij}\in \mathbb{R}^2\) is its ground truth location, and \(W\) is the width of the bounding box. Note that MPJPE measures the normalized error relative to the bounding box size \(W\), e.g., 0.1 MPJPE for 500\(\times\)500 bounding box corresponds to 50 pixel error.
Probability of correct keypoint (PCK) [2] is defined by the detection accuracy given error tolerance (the bigger, the better):\[{\rm PCK}@\epsilon = \frac{1}{17J}\sum_{j=1}^J \sum_{i=1}^{17} \delta\left(\frac{\|\widehat{\mathbf{x}}_{ij} - \mathbf{x}_{ij}\|}{W} < \epsilon\right)\]
where \(\delta(\cdot)\) is an indicator function that outputs 1 if the statement is true and zero otherwise. \(\epsilon\) is the spatial tolerance for correct detection. Note that PCK measures the detection accuracy given the normalized tolerance with respect to the bounding box width, e.g., PCK@0.2 with 200 pixel bounding box size refers to the detection accuracy where the detection with the error smaller than 40 pixels is considered as a correct detection.
Average precision (AP) measures detection precision (the bigger, the better):
\[{\rm AP}@\epsilon = \frac{1}{17J}\sum_{j=1}^J \sum_{i=1}^{17} \delta({\rm OKS}_{ij}\geq \epsilon)\]
where OKS measures keypoint similarity [3]:
\[{\rm OKS}_{ij} = \exp\left(-\frac{\|\widehat{\mathbf{x}}_{ij} - \mathbf{x}_{ij}\|^2}{2W^2k_i^2}\right)\]
where \({\rm OKS}_{ij}\) is the keypoint similarity of the \(j^{\rm th}\) image of the \(i^{\rm th}\) landmark. \(k_i\) is the \(i^{\rm th}\) landmark relative tolerance. Unlike PCK, OKS measures per landmark accuracy by taking into account per landmark variance \(k_i\) (visual ambiguity of landmarks), e.g., eye is visually less ambiguous than hip. We define \(k_i\) based on COCO keypoint challenge and augment the tail landmark such that \(k_{tail} = k_{wrist}\). The evaluation code can be found here: evaluation code link[1] Karim Iskakov, Egor Burkov, Victor Lempitsky, and Yury Malkov. Learnable Triangulation of Human Pose. International Conference on Computer Vision (ICCV), 2019.
[2] Yi Yang and Deva Ramanan. Articulated Human Detection with Flexible Mixtures of Parts. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 2013.
[3] Tsung-Yi Lin, Michael Maire, Serge Belongie, James Hays, Pietro Perona, Deva Ramanan, Piotr Dollár, Lawrence Zitnick. Microsoft COCO: Common Objects in Context. European Conference on Computer Vision (ECCV). 2014.
