Introduction
This course is an introduction to real analysis, which is the study of the real numbers and real-valued functions. Much of this course is a rigorous study of familiar topics from calculus. We will start with the principles behind the real number system, and proceed to study sequences, series, and convergence properties. The course will rigorously define notions of continuity and differentiability, and we will discuss power series and Taylor series. We will also study Riemann integration, and if there is time we will touch on metric spaces and some topology.
Course Information (pdf version)
| Instructor | Jeff Calder (Office: 1053 Evans, Email: jcalder at berkeley dot edu) |
| Lectures | Section 2: Mon, Wed, Fri, 2pm–3pm in 70 Evans Section 3: Mon, Wed, Fri, 4pm–5pm in 2 Evans |
| Office Hours | Mon: 1pm–2pm, Wed: 1pm–2pm and 3pm–4pm in 1053 Evans |
| GSI | Edward Scerbo (Office: 853 Evans) |
| GSI Office Hours | Mon: 3pm–5pm, Tue, Wed: 2pm–4pm, Thurs, Fri: 4pm–6pm in 853 Evans |
| Final Exam | Section 2: Thursday, December 18, 3pm–6pm Section 3: Thursday, December 18, 8am–11am |
| bCourses | https://bcourses.berkeley.edu |
| Textbook | Ross, Kenneth A. Elementary Analysis, 2nd Edition. Springer, 2013. |
| Additional Reading | Pugh, Charles C. Real mathematical analysis. Springer, 2002. Rudin, Walter. Principles of Mathematical Analysis. , McGraw-Hill, 1976. Lebel, Jiří. Basic Analysis. Available online |
| Homework | There will generally be weekly homework assignments posted on this website that will be due each Friday in class. Collaboration on homework is encouraged, but you must write up the solutions in your own words and cite any class members that you worked with. Homework will be graded on a scale from 0 to 10, and solutions will be posted on this website. Late homework will not be accepted, but the lowest two homework grades will be dropped. |
| Midterms | There will be two 50-minute in-class midterms scheduled for Friday, October 3 and Friday November 7. There will be no homework due on the weeks of the midterms. |
| Grade Corrections | Exam grades will be changed only if there is an obvious error on the part of the grader. Any problems with exam grades must be brought to the attention of the lecturer immediately after exams are returned. |
| Grades | The final grade will be based on homework assignments (20%), midterm I (20%), midterm II (20%), and the final exam (40%). A higher score on the final exam will erase any lower midterm score, hence your final grade will be calculated as follows: |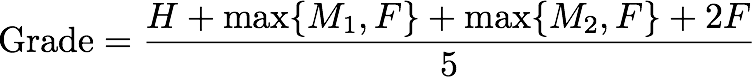
| Incomplete Grades | Incomplete “I” grades are rarely given. The only justification is a documented serious medical problem or genuine personal/family emergency. Students requesting incomplete grades must currently have a passing grade in the course. For more information, please see George Bergman's notes on incomplete grades. |
| Special Arrangements | If you are a student with a disability registered by the Disabled Student Services (DSS) on UCB campus, and if you require special arrangements for exams, please see the instructor as soon as possible. You will need to provide the DSS document detailing the special arrangements at least 10 days before any exam. |
| Academic Honesty | The mathematics department expects that students in mathematics courses will not engage in cheating or plagiarism. Cheating, plagiarism, or other forms of academic dishonesty will result in a grade of zero on the homework assignment or exam in question, and, in severe cases, a failing grade in the course and a referral to the Center for Student Conduct. Please see Michael Hutchings' description of academic honesty in mathematics courses for more information. |