Introduction
Partial differential equations (PDE) are ubiquitous in science, engineering and physics. Applications include traffic flow, heat diffusion, wave propagation, quantum mechanics, computer vision, image processing, and optimal control theory. This course is a basic introduction to partial differential equations. Topics to be covered include waves, diffusion, Laplace's equation, Fourier series and Fourier transform techniques, numerical methods for PDE, Green's functions, distributions, and some topics in nonlinear PDE, such as shock waves, conservation laws, and the calculus of variations.
The animation on the right is a numerical simulation of the mean curvature motion PDE, which moves a curve in the plane in the direction of its inward normal vector with a speed equal to its curvature. Mean curvature motion arises in physical systems that involve surface tension, such as soap film/bubbles and biological cell membranes.
Course Information
| Instructor | Jeff Calder (Office: 1053 Evans, Email: jcalder at berkeley dot edu) |
| Lectures | Mon, Wed, Fri, 8am-9am in 3106 Etcheverry |
| Office Hours | Mon, Wed, Fri, 11:30am-12:30pm in 1053 Evans Hall |
| Final Exam | Monday December 14, 2015: 7-10pm |
| Midterm Exam | Friday October 9, 2015. (In Class). |
| bCourses | https://bcourses.berkeley.edu |
| Piazza | We have a Piazza website for student discussions. To sign up for Piazza and join our class, click here . |
| Textbook | Strauss, Walter A. Partial Differential Equations: An Introduction (1st or 2nd Edition) |
| Readings | Readings will be assigned on a weekly basis and posted on the schedule page on this website. It is very important to do the readings before attending the associated lecture. |
| Homework | There will generally be weekly homework assignments posted on this website that will be due each Friday. Collaboration on homework is encouraged, but you must write up the solutions in your own words and cite any class members that you worked with. Homework will be graded on a scale from 0 to 10, and solutions to selected problems will be posted on this website. Homework will not be accepted via email and must be handed in during class. Late homework will not be accepted for any reason (but see below). Since I do not accept late or makeup homework, I will drop the two lowest homework grades when computing your final grade. This is done to account for weeks that you may be sick or unable to complete your homework for any reason. |
| Grade Corrections | Exam grades will be changed only if there is an obvious error on the part of the grader. Any problems with exam grades must be brought to the attention of the lecturer immediately after exams are returned. |
| Grades | Your final grade will be based on homework assignments (20%), the midterm exam (30%), and the final exam (50%). A higher score on the final exam replaces a lower midterm score. Hence your final grade is computed as follows: |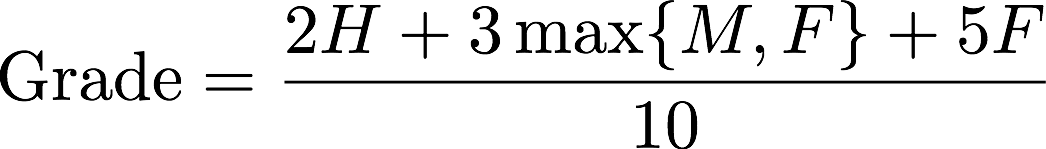
| Incomplete Grades | Incomplete “I” grades are rarely given. The only justification is a documented serious medical problem or genuine personal/family emergency. Students requesting incomplete grades must currently have a passing grade in the course. For more information, please see George Bergman's notes on incomplete grades. |
| Special Arrangements | If you are a student with a disability registered by the Disabled Student Services (DSS) on UCB campus, and if you require special arrangements for exams, please see the instructor as soon as possible. You will need to provide the DSS document detailing the special arrangements at least 10 days before any exam. |
| Academic Honesty | The mathematics department expects that students in mathematics courses will not engage in cheating or plagiarism. Cheating, plagiarism, or other forms of academic dishonesty will result in a grade of zero on the homework assignment or exam in question, and, in severe cases, a failing grade in the course and a referral to the Center for Student Conduct. Please see Michael Hutchings' description of academic honesty in mathematics courses for more information. |