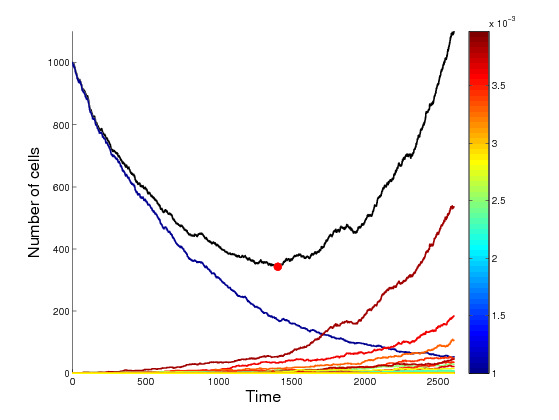
Cancer progression is driven by complex evolutionary processes occurring at the cellular scale. Tumor cells rapidly divide, acquire genetic and phenotypic variation, respond to dynamic local microenvironments, and compete for limited resources within the body. Stochasticity plays a key role in these evolutionary processes. For example, chance errors in DNA-replication during cellular division produces genetic variability that is essential in driving tumor adaptation and progression. Non-genetic stochastic transitions between cellular states produce further phenotypic variability that influences genetic progression and the fate of tumor cell populations. Developing mathematical models of these complex, interacting processes can lead to many insights into the mechanisms of cancer progression as well as treatment strategies.
Our research is focused on developing and applying stochastic models of the evolutionary dynamics driving cancer initiation, tumor progression, and treatment response. We are interested in the integration of these models with clinical and experimental data, with the ultimate goal of improving cancer treatment and prevention strategies. We are also interested in the development of mathematical theory surrounding these models, which can reveal fundamental insights about cancer evolution, enable the development of modeling and data-driven statistical frameworks for interpreting clinical and experimental data, and give rise to novel questions in probability theory.
Current research projects in our group fall under several main themes:
- Plasticity and epigenetics in tumor evolution
- Drug resistance and optimal treatment strategies
- Modeling and data-driven precision oncology
- Spatial evolution and carcinogenesis
- Tumor-microenvironment interaction and organoid modeling
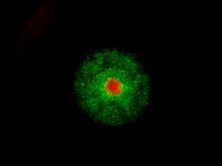
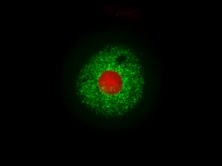 Spheroid models of resistance
outgrowth.
Spheroid models of resistance
outgrowth.S. Mumenthaler (EITM)