The following definition is a modification to this setting of that given by Conley [2,3] for flows on compact metric spaces.
Definition: A set
![]() is an attractor for
is an attractor for
![]() if
if
Some authors would call
![]() an "attracting set" and would reserve
the name "attractor" for an attracting set with further properties.
However, in this paper Conley's terminology will be followed.
an "attracting set" and would reserve
the name "attractor" for an attracting set with further properties.
However, in this paper Conley's terminology will be followed.
The preceeding definition is somewhat weak in the sense that the only
assumption on the neighborhood
![]() is that
is that
![]() . However,
this assumption is actually very strong. For example, the neighborhood
. However,
this assumption is actually very strong. For example, the neighborhood
![]() can be taken to be compact, positively invariant
can be taken to be compact, positively invariant ![]() , and
arbitrarily close to
, and
arbitrarily close to
![]() , as stated in Theorem 2.1
below. Also, the notion of
attractor corresponds to the more classical notion of "asymptotically
stable"
, as stated in Theorem 2.1
below. Also, the notion of
attractor corresponds to the more classical notion of "asymptotically
stable" ![]() .
.
We have the following theorem:
Theorem 2.1 If
![]() is a nonempty compact
invariant set, then the following statements are equivalent.
is a nonempty compact
invariant set, then the following statements are equivalent.
The next important notion is the domain of attraction ![]() .
.
The following theorems establish that the domain of
attraction of
![]() ,
,
![]() is an
open set and that every compact subset
is an
open set and that every compact subset
![]() of
of
![]() satisfies
satisfies
![]() .
.
Theorem 2.2 If
and hence
![]() is a compact positively
invariant
neighborhood of an attractor
is a compact positively
invariant
neighborhood of an attractor
![]() such that
such that
![]() , then
, then
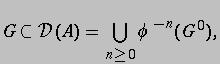
![]() is open.
is open.
Theorem 2.3 If
![]() is an attractor and if
is an attractor and if
![]() is a compact subset of
is a compact subset of
![]() , then
, then
![]() .
.
Copyright (c) 1998 by Richard
McGehee, all rights reserved.