Intensity

It is now possible to assign a precise quantity to measure the strength of attraction of an attractor. Two definitions are given, followed by a proof that the two are really the same. The first, called here the "intensity" , assigns to an attractor the supremum over all values of such that is an attractor block for . That is, every attractor block associated with has the property that the minimum distance from the image of to its complement does not exceed the intensity of . Furthermore, the intensity is the smallest such number. The second definition, called here the "chain intensity" , assigns to an attractor the supremum over all values of such that every -pseudo-orbit starting in stays in some compact subset of the domain of attraction of . That is, every -pseudo-orbit which starts in and for which does not exceed the chain intensity of remains inside the domain of attraction of . On the other hand, if does exceed the chain intensity of , then one can find an -pseudo-orbit starting on and leaving every compact subset of the domain of attraction of .

The next theorem states that the intensity and chain intensity is equal for a given attractor.

Theorem 5.1 .

Proof.

Conley was interested in the concept of "continuation" of an isolated invariant set in his study of the topological properties persisting under perturbation [3].

Given two different maps on the same space and an attractor for each map, one attractor is said to "continue immediately" to the other if a common attractor block can be found which is associated with each of the attractors.

The notion of "continuation" is obtained from the notion of "immediate continuation" by completing it to a transitive relation. In other words, an attractor for a map is said to "continue" to an attractor for another map if a sequence of maps and attractors can be found, each continuing immediately to the next.

The notion of "immediate continuation" of an attractor is closely related to its intensity of attraction. It will be convenient to introduce some notation to be used in the discussion of this relationship. If is an attractor for the map , then the intensity depends not only on the set but also on the map . If there is any doubt about which map is used in the computation of the intensity, then it will be expicitly indicated. In particular,

while

The standard metric is used on the space of maps,

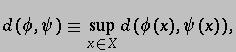
where and are both maps on . The following property is an immediate consequence of the definitions.

(5-1)

Theorem 5.2 If is an attractor for the map and if the map satisfies , then there exists an attractor for such that is an immediate continuation of .

Proof.

It is natural to ask whether there is some kind of converse to Theorem 5.2. In other words, given an attractor for the map and given an , does there exist a map satisfying such that has no attractor which is an immediate continuation of ? The answer, in this generality, is "no". Although it would be interesting to explore the conditions under which the answer is "yes", no such exploration will be undertaken here.