Pseudo-orbits

The notion of a "pseudo-orbit" has had important applications in several different areas of dynamical systems. Most important has been the concept of "shadowing", which has been used to prove the existence of orbits corresponding to symbol shifts. Hammel, Yorke and Grebogi [7,8] have exploited extensively the fact that a pseudo-orbit is the actual object computed by a computer. They are able to show rigorously that certain orbits found by simulation correspond to real orbits for the original system.

Roughly speaking, an -pseudo orbit is obtained by successively following the system, each time making an "error" of size less than .

It turns out that attractor blocks can be constructed from -pseudo-orbits. If one considers the set of all points which can be reached from an attractor by an -pseudo-orbit, then, for sufficiently small , that set is an attractor block corresponding to . This statement will be made precise and proved in this section.

The following notation will be used to denote the set of all -pseudo-orbits of length starting in the set .

It will be convenient to have a notation for the th coordinate of a pseudo-orbit. For and for , define

It is clear that -pseudo-orbits are closely related to the map . Indeed, an -pseudo-orbit is simply a sequence of points picked out of successive iterates of . More precisely, is an -pseudo-orbit if and only if

(4-1)

Observe that the notation is used. The following lemma states that points in the th iterate of under are precisely those points in the th coordinate of some -pseudo-orbit staring in .

Lemma 4.1 Fix . For every ,

Proof.

The set of all points on all -pseudo-orbits of length starting on the set will be denoted

Note that

The following lemma states that the set of all points on -pseudo-orbits starting on a set is identical to the union of iterates of under the map .

Lemma 4.2: .

Proof.

The set of all points on all -pseudo-orbits of arbitrary length will be important in what is to follow. This set will be denoted

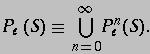
Some elementary properties of this set are collected in the following lemma.

Lemma 4.3: The following properties hold whenever they are defined.

(1)
(2)
(3)
(4)

Proof.

Note that this last property implies that the set of all points accessible by -pseudo-orbits starting on maps into itself by a distance at least . In view of Corollary 3.12, would be an attractor block if it were compact.

Corollary 4.4 If is nonempty and if is compact, then is an attractor block.

This property is exploited in the next lemma.

Lemma 4.5 Let be an attractor, let , and define . If is compact and if , then is an attractor block associated with .

Proof.

It remains to show that is close to for small .

Theorem 4.6 If is an attractor, then , as .

Proof.

An immediate consequence of this theorem is the following corollary.

Corollary 4.7 If is a neighborhood of an attractor , then there exists an such that is compact and is a subset of .