Double Cone
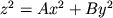
|
Display Gridlines: |
The double cone is a very important quadric surface, if for no other reason than the fact that it's used to define the so-called conics -- ellipses, hyperbolas, and parabolas -- all of which can be created as the intersection of a plane and a double cone. See any PreCalculus or Calculus textbook for pictures of this. The vertical cross sections of a double cone are hyperbolas, while the horizontal cross sections are ellipses. The picture on the left shows the cone where A=B=1. Look back at the equation for the double cone. Sometimes we manipulate it to get a single cone. If we solve for z, we end up with a plus/minus sign in front of a square root. The positive square root represents the top of the cone; the negative square root gives you an equation for the bottom. Be careful if somebody says "cone" without elaborating; they might mean "double cone" or "single cone," depending on the context. Roughly speaking, the constants A and B determine how "steep" the cone is in the x and y direction, respectively. You can get a feel from this in the second picture, which shows the portion of a cone for which x and y are between -1 and 1. You can also change the domain to a disk, which will show you the portion of the cone for which -4 ≤ z ≤ 4. After you've played around with the examples for awhile, see if you can answer the following questions:
|





