Visualization of 3D Mathematics

An ongoing project to provide visualization tools to students in multivariable calculus has led to a broader interest in the visualization of mathematics. Lately I have been particularly interested in the GeoWall, a system which uses polarized filters to display stereo images in three dimensions. As the name implies, GeoWalls have largely been used by Earth Scientists, and we are just starting to explore its potential in mathematics.

This page has a sampling of three-dimensional visualizations for use with a GeoWall, although all of them can be run in non-stereo mode as well. The first two require you to download a program and run it on your own computer; the rest can be viewed within your web browser. Please note that your GeoWall should be in "horizontal span" or "side-by-side" mode, and not "quad-buffered clone" mode.

If you are specifically interested in course materials for multivariable calculus and vector analysis, follow the "Vector Calculus" link on the menu to the left. That page also includes a number of two-dimensional visualization tools.

Standalone OpenGL applications

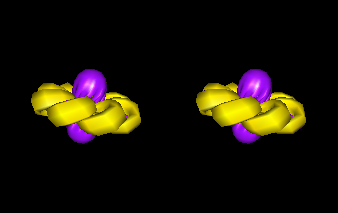
	stereoEversion is a minor fork of Michel McGuffin's sphereEversion program. It displays Thurston's eversion of the sphere, as shown in the movie Outside In. The version here includes a stereo mode for use with a GeoWall. Windows: stereoEversion.zip. Linux: stereoEversion.tar.gz. (Might compile on other platforms.)
	The Curved Spaces package by Jeff Weeks to display its images in a stereo mode. This program allows you to view and fly through flat, spherical and hyperbolic spaces. The package has been updated to include a passive 3D mode suitable for use with a GeoWall. You can download it at www.geometrygames.org.

LiveGraphics3D Materials

The following materials were all created with LiveGraphics3D, a Java applet written by Martin Kraus. If you would like to develop similar materials, you can read this online preprint of an article Martin and I wrote to describe how to create visualizations with LiveGraphics3D

Clicking on any of the following links will open the applet in a new window. Please note: depending on your browser, operating system and/or window manager, you might have to move the window to the corner of your desktop and/or resize the window to stretch across both screens.

You can use the following controls:

Click+Drag: rotate the image
Shift+Click+Drag Up/Down: zoom in/out
Home: reset the image
Double Click: stop/restart the animation (if applicable)
's' key: cycle through normal mode, parallel stereo mode, and cross-fusion stereo modes.

Any of the "GeoWall" links will automatically start in parallel stereo mode.

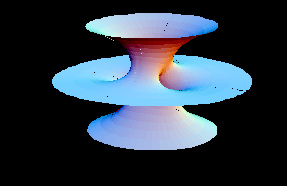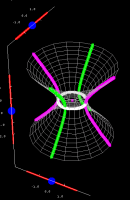		Costa Surface 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall) New: This animation demonstrates the symmetry of the Costa surface by showing how to construct it with eight pieces. Each piece is a rotation and/or reflection of the fundamental piece. 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)
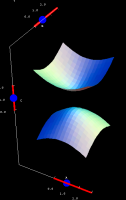		Hyperboloid of one sheet. Click and drag the blue points on the axes to view the different cross sections of the surface. This applet is part of the Interactive Gallery of Quadric Surfaces. 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)
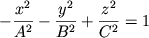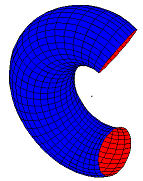		Hyperboloid of two sheets, defined by the equation: Click and drag the blue points on the axes to adjust the values of A, B, and C. This applet is part of the Interactive Gallery of Quadric Surfaces. 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)
		Gluing a rectangle into a torus (donut) using the standard two-stage process: first wrap the rectangle into a cylinder, and then glue the two ends of the cylinder together to form the torus. 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)
		Gluing a rectangle into a torus in a single stage. For topologists: this demonstrates how to visualize the single 2-cell in the "minimalist" CW-decomposition of the torus. 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)
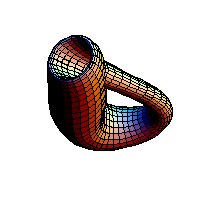		This applet provides yet another demonstrated of how demonstrates how a rectangle in uv-space is mapped onto a torus using a standard parametrization. You can click and drag the red rectangle on the left to see how its image changes on the right. 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)
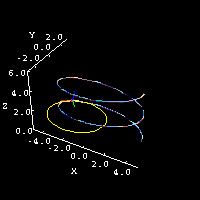		Standard immersion of a Klein Bottle 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)
		Particle moving along an elliptical helix, along with the TNB frame and osculating circle. 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)
		Often in calculus we ask students to find the volume of the intersection of two perpendicular cylinders of the same radius; we rarely ask about cylinders of different radii because it's difficult to visualize. This animation shows the intersection of a cylinder of radius 1 with a cylinder of radius 2. Rather than "drilling," I tend to describe this to students as "removing a cylindrical plug of radius 1," which is reflected in the animation. 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)
		If you wish to find the volume of the cylindrical plug in the previous example, you need to make a choice about which cross sections to examine. While it is tempting to slice the cylinder into disks, this creates problems at the top and bottom. This animation shows the correct (or at least "easiest") cross sections to use in your integral. 600 x 600 2048 x 700 (Standard Geowall) 2560 x 850 (Large Geowall)

[an error occurred while processing this directive]

This page is http://www.math.umn.edu/~rogness/visual3D/index.shtml and belongs to rogness@math.umn.edu The views and opinions expressed in this page are strictly those of the page author. The contents of this page have not been reviewed or approved by the University of Minnesota.

Many thanks to css/edge for a lot of the ideas used in the creation of this page.