Computing and applying polynomial filters. More...

#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <float.h>
#include <string.h>
#include "def.h"
#include "blaslapack.h"
#include "struct.h"
#include "internal_proto.h"

Functions
void	set_pol_def (polparams *pol)
	set default values for polparams struct. More...

int	dampcf (int m, int damping, double *jac)
	Computes damping coefficient for cheb. expansions. More...

double	dif_eval (double v, int m, double thc, double jac)
	function dif_eval(v, m, thc, jac) evaluates the difference between the right and left values of the polynomial expressed in chebyshev expansion More...

int	chebxPltd (int m, double mu, int npts, double xi, double *yi)
	function yi = chebxPltd computes yi = p_mu (xi), More...

void	chext (polparams *pol, double aIn, double bIn)
	Determines polynomial for end interval cases. More...

int	indexofSmallestElement (double *array, int size)
	Find the indexofSmallestElement in array. More...

int	rootchb (int m, double v, double jac, double tha, double thb, double mu, double thcOut)
	Finds the roots of linear combination of chebyshev polynomials. More...

int	find_pol (double intv, polparams pol)
	Sets the values in pol. More...

void	free_pol (polparams *pol)

int	ChebAv (polparams pol, double v, double y, double w)
	Computes y=P(A) v, where pn is a Cheb. polynomial expansion More...

Detailed Description

Computing and applying polynomial filters.

Definition in file chebpoly.c.

Function Documentation

int ChebAv	(	polparams *	pol,
		double *	v,
		double *	y,
		double *	w
	)

Computes y=P(A) v, where pn is a Cheb. polynomial expansion

This explicitly calls matvec, so it can be useful for implementing user-specific matrix-vector multiplication.

Parameters

	pol	Struct containing the paramenters and expansion coefficient of the polynomail.
	v	input vector
[out]	y	p(A)v

Workspace

Parameters

w	Work vector of length 3*n [allocate before call]
v	is untouched

Definition at line 510 of file chebpoly.c.

References _polparams::cc, DAXPY(), _polparams::dd, _polparams::deg, DSCAL(), evsl_timer(), evsldata, evslstat, _evsldata::ifGenEv, _polparams::mu, _evsldata::n, _evslstat::n_polAv, _evslstat::t_polAv, and _evslstat::t_sth.

Referenced by ChebLanNr(), ChebLanTr(), and ChebSI().

Here is the call graph for this function:

Here is the caller graph for this function:

int chebxPltd	(	int	m,
		double *	mu,
		int	npts,
		double *	xi,
		double *	yi
	)

function yi = chebxPltd computes yi = p_mu (xi),

where xi is a vectors of values. This can used for plotting the filter given by mu for example – Jackson (or other) dampings is not explicitly used here but is assumed to be multiplied by mu outside this routine.

Parameters

m	degree of the polynomial = length(mu)-1
mu	Chev. expansion coefficients in KPM method
npts	= number of points in xi, yi
xi	= a vector of values where p(xi) is to be computed.

Warning: Note xi's must be in [-1 1]

Parameters

[out] yi = pn(xi(:) )

Returns: 0

Definition at line 106 of file chebpoly.c.

References DAXPY(), Malloc, and vecset().

Referenced by find_pol(), and lsPol().

Here is the call graph for this function:

Here is the caller graph for this function:

void chext	(	polparams *	pol,
		double	aIn,
		double	bIn
	)

Determines polynomial for end interval cases.

In these cases, polynomial is just a scaled Chebyshev polynomial. However we need to express it in the same basis as in the other (middle interval) cases. This function determines this expansion

Parameters

aIn	The start index of the transformed interval
bIn	The end index of the transformed interval

Note: [aIn, bIn] is the transformed interval

Parameters

pol	A struct containing the parameters of polynomial.

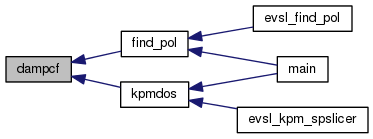
Modifies mu Expansion coefficients of best polynomial found. deg: Degree of polynomial gam: Site of delta function that is expanded. Accurate 'balancing' is done: If p(t) is best approximation to delta function at gam then gam is selected so that p(a)=p(b) - within the tolerance tolBal (set in this function to 1.e-10) bar: If $P(\lambda_{i}) \geq$ bar, accept eigenvalue as belonging to interval; else reject.

Note: [a b] is now "interval for eigenvalues to damp", [aIn, bIn] is the interval of interest del is used to expand interval of interest slightly so that pn(t)<bar by some margin.

Definition at line 171 of file chebpoly.c.

References _polparams::bar, Calloc, _polparams::deg, _polparams::gam, _polparams::max_deg, _polparams::mu, and _polparams::thresh_ext.

Referenced by find_pol().

Here is the caller graph for this function:

int dampcf	(	int	m,
		int	damping,
		double *	jac
	)

Computes damping coefficient for cheb. expansions.

Parameters

	damping	== 0 –> no damping == 1 –> Jackson == 2 –> Lanczos sigma damping
	m	degree of the polynomial
[out]	jac	output array of dampened coefficients

Returns: 0

Definition at line 40 of file chebpoly.c.

References PI.

Referenced by find_pol(), and kpmdos().

Here is the caller graph for this function:

double dif_eval	(	double *	v,
		int	m,
		double	thc,
		double *	jac
	)

function dif_eval(v, m, thc, jac) evaluates the difference between the right and left values of the polynomial expressed in chebyshev expansion

Parameters

v	vector of coefficients [see paper]
m	degree
thc	angle theta corresponding to peak of polynomial
jac	vector of damping coefficients

Definition at line 79 of file chebpoly.c.

Referenced by rootchb().

Here is the caller graph for this function:

int find_pol	(	double *	intv,
		polparams *	pol
	)

Sets the values in pol.

Parameters

intv	An array of length 4, [intv[0, intv[1]] is the interval of desired eigenvalues. [intv[2], intv[3]] is the global interval of all eigenvalues it must contain all eigenvalues of A.
pol	The polynomial struct to set the values of.

Warning: Set the following values of pol
mu Expansion coefficients of best polynomial found
gam Site of delta function that is expanded. accurate 'balancing' is done: if p(t) is best approximation to delta function at gam then gam is selected so that p(a)=p(b) - within the tolerance tolBal (set in this function to 1.e-10)
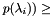bar If $p(\lambda_i)) \geq$ bar, accept eignevalue as belonging to interval; else reject.
deg degree of polynomial
dd half-width and...
cc ... Center of interval containing all eigenvalues [these are used by ChebAv]

Definition at line 361 of file chebpoly.c.

References _polparams::bar, _polparams::cc, chebxPltd(), chext(), dampcf(), _polparams::damping, _polparams::dd, _polparams::deg, _polparams::gam, _polparams::intvtol, Malloc, max, _polparams::max_deg, min, _polparams::min_deg, _polparams::mu, rootchb(), _polparams::thresh_int, and _polparams::type.

Referenced by evsl_find_pol(), and main().

Here is the call graph for this function:

Here is the caller graph for this function:

void free_pol ( polparams * pol )

Definition at line 488 of file chebpoly.c.

References _polparams::mu.

Referenced by evsl_free_pol(), and main().

Here is the caller graph for this function:

int indexofSmallestElement	(	double *	array,
		int	size
	)

Find the indexofSmallestElement in array.

Parameters

array	Array to find the smallest index of
size	size of the arry

Returns: index of smallest entry in array

Definition at line 268 of file chebpoly.c.

int rootchb	(	int	m,
		double *	v,
		double *	jac,
		double	tha,
		double	thb,
		double *	mu,
		double *	thcOut
	)

Finds the roots of linear combination of chebyshev polynomials.

Parameters

	m	degree of polynomial
	v	difference between cosines on left and right [(3.12) in paper]
	jac	damping coefficients
	tha	theta_a [refer to paper]
	thb	theta_b [refer to paper]
	mu	expansion coefficients.
[out]	thcOut	value of theta_c

Definition at line 287 of file chebpoly.c.

References dif_eval().

Referenced by find_pol().

Here is the call graph for this function:

Here is the caller graph for this function:

void set_pol_def ( polparams * pol )

set default values for polparams struct.

Definition at line 18 of file chebpoly.c.

References _polparams::damping, _polparams::deg, _polparams::intvtol, _polparams::max_deg, _polparams::min_deg, _polparams::mu, _polparams::thresh_ext, _polparams::thresh_int, and _polparams::tol.

Referenced by evsl_find_pol(), and main().

Here is the caller graph for this function:

Functions

Detailed Description

Function Documentation