This file contains function prototypes and constant definitions internally used in EVSL. More...

#include <stdio.h>
#include <complex.h>
#include "evsl.h"
#include "struct.h"

This graph shows which files directly or indirectly include this file:

Functions
int	chebxCoefd (int m, double gam, int damping, double *mu)

int	dampcf (int m, int damping, double *jac)
	Computes damping coefficient for cheb. expansions. More...

int	chebxPltd (int m, double mu, int n, double xi, double *yi)
	function yi = chebxPltd computes yi = p_mu (xi), More...

int	ChebAv (polparams pol, double v, double y, double w)
	Computes y=P(A) v, where pn is a Cheb. polynomial expansion More...

void	chext (polparams *pol, double aIn, double bIn)
	Determines polynomial for end interval cases. More...

int	apfun (const double c, const double h, const double xi, double(ffun)(double), const int npts, double *yi)

double	rec (const double a)

double	isqrt (const double a)

int	pnav (double mu, const int m, const double cc, const double dd, double v, double y, double w)

int	lsPol (double(ffun)(double), BSolDataPol pol)

void	savemat (csrMat A, const char fn)

void	savedensemat (double A, int lda, int m, int n, const char fn)

void	save_vec (int n, const double *x, const char fn[])

int	SymmTridEig (double eigVal, double eigVec, int n, const double diag, const double sdiag)
	compute all eigenvalues and eigenvectors of a symmetric tridiagonal matrix More...

int	SymmTridEigS (double eigVal, double eigVec, int n, double vl, double vu, int nevO, const double diag, const double *sdiag)
	compute eigenvalues and eigenvectors of a symmetric tridiagonal matrix in a slice More...

void	SymEigenSolver (int n, double A, int lda, double Q, int ldq, double *lam)
	interface to LAPACK SYMMETRIC EIGEN-SOLVER More...

void	CGS_DGKS (int n, int k, int i_max, double Q, double v, double nrmv, double w)
	Classical GS reortho with Daniel, Gragg, Kaufman, Stewart test. More...

void	CGS_DGKS2 (int n, int k, int i_max, double Z, double Q, double v, double w)
	Classical GS reortho. No test. just do i_max times used in generalized ev problems. More...

void	orth (double V, int n, int k, double Vo, double *work)
	Orthogonalize columns of n-by-k matrix V. More...

void	contQuad (int method, int n, complex double *zk)
	Compute the locations of the poles. More...

void	ratf2p2 (int n, int mulp, complex double zk, complex double alp, int m, double z, double *x)
	Compute the function value of the multiple pole rational filter at real locations. More...

void	pfe2 (complex double s1, complex double s2, int k1, int k2, complex double alp, complex double bet)
	Get the fraction expansion of 1/[(z-s1)^k1 (z-s2)^k2]. More...

complex double	integg2 (complex double s1, complex double s2, complex double alp, int k1, complex double bet, int k2, double a, double b)
	Integration of 1/[(z-s1)^k1 (z-s2)^k2] from a to b. More...

void	weights (int n, complex double zk, int pow, double lambda, complex double *omega)
	Compute the LS weight for each multiple pole. More...

int	scaleweigthts (int n, double a, double b, complex double zk, int pow, complex double *omegaM)
	Compute the weights and pole locations on [a, b]. More...

void	RatFiltApply (int n, ratparams rat, double b, double x, double w3)
	Apply rational filter R to a vetor b. More...

void	simpson (double xi, double yi, int npts)

void	matvec_csr (double x, double y, void *data)
	matvec for a CSR matrix, y = Ax. void data points to csrMat, compatible form with EVSLMatvec (see struct.h) More...

void	csr_resize (int nrow, int ncol, int nnz, csrMat *csr)
	memory allocation for csr matrix More...

void	sortrow (csrMat *A)
	Sort each row of a csr by increasing column order By double transposition. More...

int	matadd (double alp, double bet, csrMat A, csrMat B, csrMat C, int mapA, int *mapB)
	matrix addition C = alp * A + bet * B More...

int	speye (int n, csrMat *A)
	return an identity matrix of dimension n More...

void	triuCsr (csrMat A, csrMat U)

int	time_seeder ()
	Uses the timer to generate a seed to be used for srand. More...

void	vecset (int n, double t, double *v)

void	vec_perm (int n, int p, double x, double *y)

void	vec_iperm (int n, int p, double x, double *y)

Detailed Description

This file contains function prototypes and constant definitions internally used in EVSL.

Definition in file internal_proto.h.

Function Documentation

int apfun	(	const double	c,
		const double	h,
		const double *const	xi,
		double(*)(double)	ffun,
		const int	npts,
		double *	yi
	)

Evalutes ffun at the xi's. Assumes a transformation of original inetrval [a b] into [-1, 1] so: the xi's are between -1 and 1

Parameters

[in]	c	Value to increase xi's by
[in]	h	Value to scale xi's by
[in]	*xi	Points for which to evaluate ffun at
[in]	npts	Number of points in xi to evaluate
[in]	ffun	Function to evaluate
[out]	yi	ffun evaluated at xi's

Definition at line 83 of file dos_utils.c.

References ffun().

Referenced by lsPol().

Here is the call graph for this function:

Here is the caller graph for this function:

void CGS_DGKS	(	int	n,
		int	k,
		int	i_max,
		double *	Q,
		double *	v,
		double *	nrmv,
		double *	w
	)

Classical GS reortho with Daniel, Gragg, Kaufman, Stewart test.

Definition at line 195 of file misc_la.c.

References DAXPY(), DDOT(), DGEMV(), DNRM2(), evsl_timer(), evslstat, and _evslstat::t_reorth.

Referenced by ChebLanNr(), ChebLanTr(), LanDosG(), LanTrbounds(), orth(), RatLanNr(), and RatLanTr().

Here is the call graph for this function:

Here is the caller graph for this function:

void CGS_DGKS2	(	int	n,
		int	k,
		int	i_max,
		double *	Z,
		double *	Q,
		double *	v,
		double *	w
	)

Classical GS reortho. No test. just do i_max times used in generalized ev problems.

Definition at line 235 of file misc_la.c.

References DAXPY(), DDOT(), DGEMV(), evsl_timer(), evslstat, and _evslstat::t_reorth.

Referenced by ChebLanNr(), ChebLanTr(), LanDosG(), LanTrbounds(), RatLanNr(), and RatLanTr().

Here is the call graph for this function:

Here is the caller graph for this function:

int ChebAv	(	polparams *	pol,
		double *	v,
		double *	y,
		double *	w
	)

Computes y=P(A) v, where pn is a Cheb. polynomial expansion

This explicitly calls matvec, so it can be useful for implementing user-specific matrix-vector multiplication.

Parameters

	pol	Struct containing the paramenters and expansion coefficient of the polynomail.
	v	input vector
[out]	y	p(A)v

Workspace

Parameters

w	Work vector of length 3*n [allocate before call]
v	is untouched

Definition at line 510 of file chebpoly.c.

References _polparams::cc, DAXPY(), _polparams::dd, _polparams::deg, DSCAL(), evsl_timer(), evsldata, evslstat, _evsldata::ifGenEv, _polparams::mu, _evsldata::n, _evslstat::n_polAv, _evslstat::t_polAv, and _evslstat::t_sth.

Referenced by ChebLanNr(), ChebLanTr(), and ChebSI().

Here is the call graph for this function:

Here is the caller graph for this function:

int chebxCoefd	(	int	m,
		double	gam,
		int	damping,
		double *	mu
	)

int chebxPltd	(	int	m,
		double *	mu,
		int	npts,
		double *	xi,
		double *	yi
	)

function yi = chebxPltd computes yi = p_mu (xi),

where xi is a vectors of values. This can used for plotting the filter given by mu for example – Jackson (or other) dampings is not explicitly used here but is assumed to be multiplied by mu outside this routine.

Parameters

m	degree of the polynomial = length(mu)-1
mu	Chev. expansion coefficients in KPM method
npts	= number of points in xi, yi
xi	= a vector of values where p(xi) is to be computed.

Warning: Note xi's must be in [-1 1]

Parameters

[out] yi = pn(xi(:) )

Returns: 0

Definition at line 106 of file chebpoly.c.

References DAXPY(), Malloc, and vecset().

Referenced by find_pol(), and lsPol().

Here is the call graph for this function:

Here is the caller graph for this function:

void chext	(	polparams *	pol,
		double	aIn,
		double	bIn
	)

Determines polynomial for end interval cases.

In these cases, polynomial is just a scaled Chebyshev polynomial. However we need to express it in the same basis as in the other (middle interval) cases. This function determines this expansion

Parameters

aIn	The start index of the transformed interval
bIn	The end index of the transformed interval

Note: [aIn, bIn] is the transformed interval

Parameters

pol	A struct containing the parameters of polynomial.

Modifies mu Expansion coefficients of best polynomial found. deg: Degree of polynomial gam: Site of delta function that is expanded. Accurate 'balancing' is done: If p(t) is best approximation to delta function at gam then gam is selected so that p(a)=p(b) - within the tolerance tolBal (set in this function to 1.e-10) bar: If $P(\lambda_{i}) \geq$ bar, accept eigenvalue as belonging to interval; else reject.

Note: [a b] is now "interval for eigenvalues to damp", [aIn, bIn] is the interval of interest del is used to expand interval of interest slightly so that pn(t)<bar by some margin.

Definition at line 171 of file chebpoly.c.

References _polparams::bar, Calloc, _polparams::deg, _polparams::gam, _polparams::max_deg, _polparams::mu, and _polparams::thresh_ext.

Referenced by find_pol().

Here is the caller graph for this function:

void contQuad	(	int	method,
		int	n,
		complex double *	zk
	)

Compute the locations of the poles.

----------------------— Cauchy integration-based filter -----------—

Parameters

	method	0 for Guass Legendre; 1 for midpoint
	n	Number of poles in the upper half plane
[out]	zk	Vector of pole locations

Definition at line 23 of file ratfilter.c.

References DSTEV(), M_PI, and Malloc.

Referenced by find_ratf().

Here is the call graph for this function:

Here is the caller graph for this function:

void csr_resize	(	int	nrow,
		int	ncol,
		int	nnz,
		csrMat *	csr
	)

memory allocation for csr matrix

Definition at line 79 of file spmat.c.

References _csrMat::a, _csrMat::ia, _csrMat::ja, Malloc, _csrMat::ncols, _csrMat::nrows, and _csrMat::owndata.

Referenced by cooMat_to_csrMat(), csr_copy(), matadd(), speye(), and triuCsr().

Here is the caller graph for this function:

int dampcf	(	int	m,
		int	damping,
		double *	jac
	)

Computes damping coefficient for cheb. expansions.

Parameters

	damping	== 0 –> no damping == 1 –> Jackson == 2 –> Lanczos sigma damping
	m	degree of the polynomial
[out]	jac	output array of dampened coefficients

Returns: 0

Definition at line 40 of file chebpoly.c.

References PI.

Referenced by find_pol(), and kpmdos().

Here is the caller graph for this function:

complex double integg2	(	complex double	s1,
		complex double	s2,
		complex double *	alp,
		int	k1,
		complex double *	bet,
		int	k2,
		double	a,
		double	b
	)

Integration of 1/[(z-s1)^k1 (z-s2)^k2] from a to b.

Definition at line 129 of file ratfilter.c.

Referenced by weights().

Here is the caller graph for this function:

double isqrt ( const double a )

Definition at line 17 of file dos_utils.c.

Referenced by SetupPolSqrt().

Here is the caller graph for this function:

int lsPol	(	double(*)(double)	ffun,
		BSolDataPol *	pol
	)

Finds the least-square polynomial approximation to function ffun in interval given by intv

Parameters

[in]	ffun	Function to generate an approximation for
[in,out]	pol	polparams struct \ Contains: cc = (a + b) / 2 \ dd = (b - a) / 2 \ mu = coefficients \ max_deg = number of coefficients

Definition at line 168 of file dos_utils.c.

References apfun(), _BSolDataPol::cc, chebxPltd(), _BSolDataPol::dd, _BSolDataPol::deg, ffun(), _BSolDataPol::intv, linspace(), Malloc, _BSolDataPol::max_deg, _BSolDataPol::mu, and PI.

Referenced by SetupBPol().

Here is the call graph for this function:

Here is the caller graph for this function:

int matadd	(	double	alp,
		double	bet,
		csrMat *	A,
		csrMat *	B,
		csrMat *	C,
		int *	mapA,
		int *	mapB
	)

matrix addition C = alp * A + bet * B

Parameters

[in]	alp
[in]	bet
[in]	A
[in]	B
[out]	C

Warning: the nz pattern of C will be union of those of A and B. no cancellation will be considered; A and B MUST be sorted, on output C will be sorted as well

Parameters

[out]	mapA	(of size nnzA or null), mapB (of size nnzB or null) if not null, on output mapA contains the location of each nonzero of A in the CSR matrix C, i.e. mapA[i] is the position of the corresponding entry in C.ja and C.a for entry in A.ja[i] and A.a[i]
[out]	mapB	the same as mapA

Definition at line 307 of file spmat.c.

References _csrMat::a, csr_resize(), _csrMat::ia, _csrMat::ja, matadd_insert(), _csrMat::ncols, _csrMat::nrows, and Realloc.

Referenced by SetupASIGMABSolDirect().

Here is the call graph for this function:

Here is the caller graph for this function:

void matvec_csr	(	double *	x,
		double *	y,
		void *	data
	)

matvec for a CSR matrix, y = A*x. void *data points to csrMat, compatible form with EVSLMatvec (see struct.h)

Definition at line 247 of file spmat.c.

References _csrMat::a, dcsrmv(), _csrMat::ia, _csrMat::ja, _csrMat::ncols, and _csrMat::nrows.

Referenced by SetAMatrix(), and SetBMatrix().

Here is the call graph for this function:

Here is the caller graph for this function:

void orth	(	double *	V,
		int	n,
		int	k,
		double *	Vo,
		double *	work
	)

Orthogonalize columns of n-by-k matrix V.

Parameters

	n	number of rows in V
	V	Matrix which columns are to be orthogonalized
	k	number of columns in V
[out]	Vo	Output matrix
	work	work

Definition at line 269 of file misc_la.c.

References CGS_DGKS(), DCOPY(), DDOT(), DSCAL(), and NGS_MAX.

Referenced by ChebSI().

Here is the call graph for this function:

Here is the caller graph for this function:

void pfe2	(	complex double	s1,
		complex double	s2,
		int	k1,
		int	k2,
		complex double *	alp,
		complex double *	bet
	)

Get the fraction expansion of 1/[(z-s1)^k1 (z-s2)^k2].

Definition at line 95 of file ratfilter.c.

Referenced by weights().

Here is the caller graph for this function:

int pnav	(	double *	mu,
		const int	m,
		const double	cc,
		const double	dd,
		double *	v,
		double *	y,
		double *	w
	)

Computes y=P(A) v, where pn is a Cheb. polynomial expansion

This explicitly calls matvec, so it can be useful for implementing user-specific matrix-vector multiplication.

Parameters

[in]	mu	Coefficents of the cheb. polynomial (size m+1)
[in]	cc	cc member of pol struct
[in]	dd	dd member of pol struct
[in]	m	m member of pol struct
[in]	v	input vector
[out]	y	p(A)v

Workspace

Parameters

[in,out] w Work vector of length 3*n [allocate before call

Definition at line 109 of file dos_utils.c.

References evsldata, and _evsldata::n.

Referenced by BSolPol().

Here is the caller graph for this function:

void ratf2p2	(	int	n,
		int *	mulp,
		complex double *	zk,
		complex double *	alp,
		int	m,
		double *	z,
		double *	xx
	)

Compute the function value of the multiple pole rational filter at real locations.

---------------—Multiple pole rational filter evaluation -----------—

Parameters

	n	number of the pole
	mulp	multiplicity of the pole
	zk	array containing the poles.
	alp	fractional expansion coefficients
	m	number of locations to be evaluated
	z	real locations to be evaluated
[out]	xx	: function values at real locations z

Definition at line 69 of file ratfilter.c.

Referenced by scaleweigthts(), and weights().

Here is the caller graph for this function:

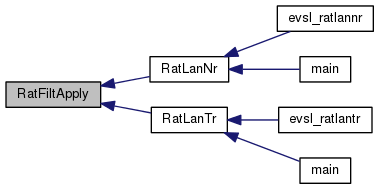
void RatFiltApply	(	int	n,
		ratparams *	rat,
		double *	b,
		double *	x,
		double *	w6
	)

Apply rational filter R to a vetor b.

For generalized e.v problem x = L' * (A-SB) \ L*b [w:=work] x = L * b w = (A-sB) \ x x = L' * w

Parameters

[in]	rat	ratparams struct
[in]	n	Length of array
[in]	b	x = L * b
	w6	Work array of size 4n for standard ev problem, size 6n for generalized ev problem
[out]	x	Becomes R(A)b

Definition at line 448 of file ratfilter.c.

References _ratparams::ASIGBsol, DAXPY(), DSCAL(), evsl_timer(), evsldata, evslstat, _evsldata::ifGenEv, _ratparams::mulp, _evslstat::n_ratAv, _ratparams::num, _ratparams::omega, and _evslstat::t_ratAv.

Referenced by RatLanNr(), and RatLanTr().

Here is the call graph for this function:

Here is the caller graph for this function:

double rec ( const double a )

Definition at line 15 of file dos_utils.c.

Referenced by SetupPolRec().

Here is the caller graph for this function:

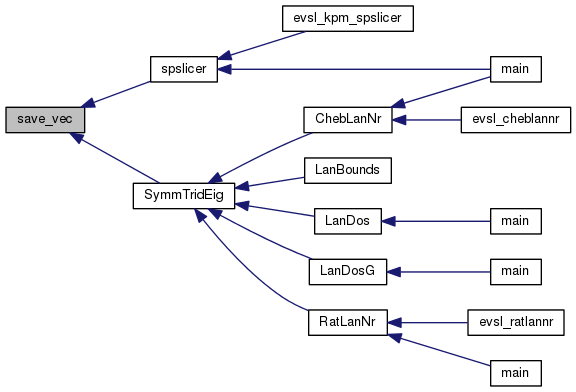
void save_vec	(	int	n,
		const double *	x,
		const char	fn[]
	)

Definition at line 38 of file dumps.c.

Referenced by spslicer(), and SymmTridEig().

Here is the caller graph for this function:

void savedensemat	(	double *	A,
		int	lda,
		int	m,
		int	n,
		const char *	fn
	)

Definition at line 49 of file dumps.c.

void savemat	(	csrMat *	A,
		const char *	fn
	)

Definition at line 33 of file dumps.c.

References _csrMat::a, _csrMat::ia, _csrMat::ja, _csrMat::ncols, _csrMat::nrows, and save_mtx_basic().

Here is the call graph for this function:

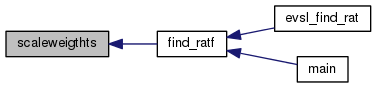
int scaleweigthts	(	int	n,
		double	a,
		double	b,
		complex double *	zk,
		int *	mulp,
		complex double *	omegaM
	)

Compute the weights and pole locations on [a, b].

---------------—Transform poles and weights computed on [-1, 1] to [a, b] -------—

Parameters

	n	number of poles used in the upper half plane
	a,b	[a, b] is the interval of desired eigenvalues
	zk	location of the poles
	mulp	multiplicity of the poles
[out]	omegaM	multiple LS weights

Definition at line 313 of file ratfilter.c.

References ratf2p2().

Referenced by find_ratf().

Here is the call graph for this function:

Here is the caller graph for this function:

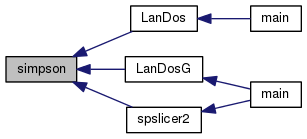
void simpson	(	double *	xi,
		double *	yi,
		int	npts
	)

This function computes the integrals from xi[0] to xi[j] for j=0:npts-1

Parameters

[in]	xi	npts equally space points
[in]	yi	values of a function f at the xi
[in]	npts	number of sample points

In-place version.

Definition at line 27 of file simpson.c.

Referenced by LanDos(), LanDosG(), and spslicer2().

Here is the caller graph for this function:

void sortrow ( csrMat * A )

Sort each row of a csr by increasing column order By double transposition.

Definition at line 56 of file spmat.c.

References _csrMat::a, csrcsc(), _csrMat::ia, _csrMat::ja, Malloc, _csrMat::ncols, and _csrMat::nrows.

Referenced by cooMat_to_csrMat().

Here is the call graph for this function:

Here is the caller graph for this function:

int speye	(	int	n,
		csrMat *	A
	)

return an identity matrix of dimension n

Definition at line 357 of file spmat.c.

References _csrMat::a, csr_resize(), _csrMat::ia, and _csrMat::ja.

Referenced by SetupASIGMABSolDirect().

Here is the call graph for this function:

Here is the caller graph for this function:

void SymEigenSolver	(	int	n,
		double *	A,
		int	lda,
		double *	Q,
		int	ldq,
		double *	lam
	)

interface to LAPACK SYMMETRIC EIGEN-SOLVER

Definition at line 156 of file misc_la.c.

References DSYEV(), evsl_timer(), evslstat, Malloc, and _evslstat::t_eig.

Referenced by ChebLanTr(), ChebSI(), LanTrbounds(), and RatLanTr().

Here is the call graph for this function:

Here is the caller graph for this function:

int SymmTridEig	(	double *	eigVal,
		double *	eigVec,
		int	n,
		const double *	diag,
		const double *	sdiag
	)

compute all eigenvalues and eigenvectors of a symmetric tridiagonal matrix

Parameters

	n	The dimension of the symmetric tridiagonal matrix
	diag[],sdiag[]	Define the symmetric tridiagonal matrix: the diagonal elements are diag[0,...,n-1] in order and the subdiagonal elements are sdiag[0,...,n-2] in order
[out]	eigVal	The output vector of length n containing all eigenvalues in ascending order
[out]	eigVec	The output n-by-n matrix with columns as eigenvectors, in the order as elements in eigVal. If NULL, then no eigenvector will be computed

Returns: The flag returned by the
LAPACK routine DSTEV() (if double) or stev_() (if float)

Definition at line 36 of file misc_la.c.

References DSTEV(), evsl_timer(), evslstat, Malloc, save_vec(), and _evslstat::t_eig.

Referenced by ChebLanNr(), LanBounds(), LanDos(), LanDosG(), and RatLanNr().

Here is the call graph for this function:

Here is the caller graph for this function:

int SymmTridEigS	(	double *	eigVal,
		double *	eigVec,
		int	n,
		double	vl,
		double	vu,
		int *	nevO,
		const double *	diag,
		const double *	sdiag
	)

compute eigenvalues and eigenvectors of a symmetric tridiagonal matrix in a slice

Parameters

	n	The dimension of the symmetric tridiagonal matrix
	diag[],sdiag[]	define the symmetric tridiagonal matrix.
[out]	eigVal	Total number of eigenvalues found.
[out]	eigVec	The first M elements contain teh selected eigenvalues in ascending oredr
[in]	vl	If range='V', The lower bound of the interval to be searched for eigen values.
[in]	vu	If range='V', the upper bound of the interval to be searched for eigenvalues.
[in]	nevO	If range='I', the index of the smallest eigen value to be returned.

This routine computes selected eigenvalues/vectors as specified by a

range of values. This is a wrapper to the LAPACK routine DSTEMR().

Definition at line 93 of file misc_la.c.

References Calloc, DSTEMR(), evsl_timer(), evslstat, Malloc, and _evslstat::t_eig.

Referenced by ChebLanNr(), and RatLanNr().

Here is the call graph for this function:

Here is the caller graph for this function:

int time_seeder ( )

Uses the timer to generate a seed to be used for srand.

Definition at line 30 of file mactime.c.

References evsl_timer().

Referenced by kpmdos().

Here is the call graph for this function:

Here is the caller graph for this function:

void triuCsr	(	csrMat *	A,
		csrMat *	U
	)

Definition at line 424 of file spmat.c.

References _csrMat::a, CHKERR, csr_resize(), EVSL_Int, EVSL_Unsigned, _csrMat::ia, _csrMat::ja, _csrMat::ncols, and _csrMat::nrows.

Here is the call graph for this function:

void vec_iperm	(	int	n,
		int *	p,
		double *	x,
		double *	y
	)

Definition at line 127 of file vect.c.

void vec_perm	(	int	n,
		int *	p,
		double *	x,
		double *	y
	)

Definition at line 114 of file vect.c.

void vecset	(	int	n,
		double	t,
		double *	v
	)

Definition at line 48 of file vect.c.

Referenced by chebxPltd().

Here is the caller graph for this function:

void weights	(	int	n,
		complex double *	zk,
		int *	mulp,
		double	lambda,
		complex double *	omega
	)

Compute the LS weight for each multiple pole.

---------------—multiple pole LS rational filter weights-----------—

Parameters

	n	number of poles in the upper half plane
	zk	pole locations
	mulp	multiplicity of each pole
	lambda	LS integration weight for [-1, 1]
[out]	omega	LS weight for each pole

Definition at line 169 of file ratfilter.c.

References integg2(), Malloc, pfe2(), ratf2p2(), and ZGESV().

Referenced by find_ratf().

Here is the call graph for this function:

Here is the caller graph for this function:

Functions

Detailed Description

Function Documentation

LAPACK routine DSTEV() (if double) or stev_() (if float)

range of values. This is a wrapper to the LAPACK routine DSTEMR().