Spectrum slicing. More...

#include <math.h>
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <float.h>
#include "def.h"
#include "blaslapack.h"
#include "struct.h"
#include "internal_proto.h"

Functions
int	kpmdos (int Mdeg, int damping, int nvec, double intv, double mu, double *ecnt)
	This function computes the coefficients of the density of states in the chebyshev basis. It also returns the estimated number of eigenvalues in the interval given by intv. More...

void	intChx (const int Mdeg, double mu, const int npts, double xi, double *yi)
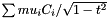	Computes the integrals $\int_{xi[0]}^{xi[j]} p(t) dt$ where p(t) is the approximate DOS as given in the KPM method in the expanded form: $\sum mu_i C_i /\sqrt{1-t^2}$ . More...

int	spslicer (double sli, double mu, int Mdeg, double *intv, int n_int, int npts)
	given the dos function defined by mu find a partitioning of sub-interval [a,b] of the spectrum so each subinterval has about the same number of eigenvalues Mdeg = degree.. mu is of length Mdeg+1 [0—> Mdeg] on return [ sli[i],sli[i+1] ] is a subinterval (slice). More...

Detailed Description

Spectrum slicing.

Definition in file spslice.c.

Function Documentation

void intChx	(	const int	Mdeg,
		double *	mu,
		const int	npts,
		double *	xi,
		double *	yi
	)

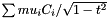Computes the integrals $\int_{xi[0]}^{xi[j]} p(t) dt$ where p(t) is the approximate DOS as given in the KPM method in the expanded form: $\sum mu_i C_i /\sqrt{1-t^2}$ .

Definition at line 154 of file spslice.c.

References Malloc.

Referenced by spslicer().

Here is the caller graph for this function:

int kpmdos	(	int	Mdeg,
		int	damping,
		int	nvec,
		double *	intv,
		double *	mu,
		double *	ecnt
	)

This function computes the coefficients of the density of states in the chebyshev basis. It also returns the estimated number of eigenvalues in the interval given by intv.

Parameters

	Mdeg	degree of polynomial to be used.
	damping	type of damping to be used [0=none,1=jackson,2=sigma]
	nvec	number of random vectors to use for sampling
	intv	an array of length 4 [intv[0] intv[1]] is the interval of desired eigenvalues that must be cut (sliced) into n_int sub-intervals [intv[2],intv[3]] is the global interval of eigenvalues it must contain all eigenvalues of A
[out]	mu	array of Chebyshev coefficients
[out]	ecnt	estimated num of eigenvalues in the interval of interest

Definition at line 32 of file spslice.c.

References dampcf(), DDOT(), DNRM2(), DSCAL(), evsldata, _evsldata::ifGenEv, Malloc, max, min, _evsldata::n, PI, rand_double(), and time_seeder().

Referenced by evsl_kpm_spslicer(), and main().

Here is the call graph for this function:

Here is the caller graph for this function:

int spslicer	(	double *	sli,
		double *	mu,
		int	Mdeg,
		double *	intv,
		int	n_int,
		int	npts
	)

given the dos function defined by mu find a partitioning of sub-interval [a,b] of the spectrum so each subinterval has about the same number of eigenvalues Mdeg = degree.. mu is of length Mdeg+1 [0—> Mdeg] on return [ sli[i],sli[i+1] ] is a subinterval (slice).

Parameters

*sli	see above (output)
*mu	coeffs of polynomial (input)
Mdeg	degree of polynomial (input)
*intv	an array of length 4 [intv[0] intv[1]] is the interval of desired eigenvalues that must be cut (sliced) into n_int sub-intervals [intv[2],intv[3]] is the global interval of eigenvalues it must contain all eigenvalues of A
n_int	number of slices wanted (input)
npts	number of points to use for discretizing the interval [a b]. The more points the more accurate the intervals. it is recommended to set npts to a few times the number of eigenvalues in the interval [a b] (input).

Definition at line 204 of file spslice.c.

References intChx(), linspace(), Malloc, max, min, and save_vec().

Referenced by evsl_kpm_spslicer(), and main().

Here is the call graph for this function:

Here is the caller graph for this function:

Functions

Detailed Description

Function Documentation