Home Page of Svitlana Mayboroda: teaching and
mentoring
Publications
Conferences and
Workshops organized
Curriculum Vitae
Students,
postdocs, teaching
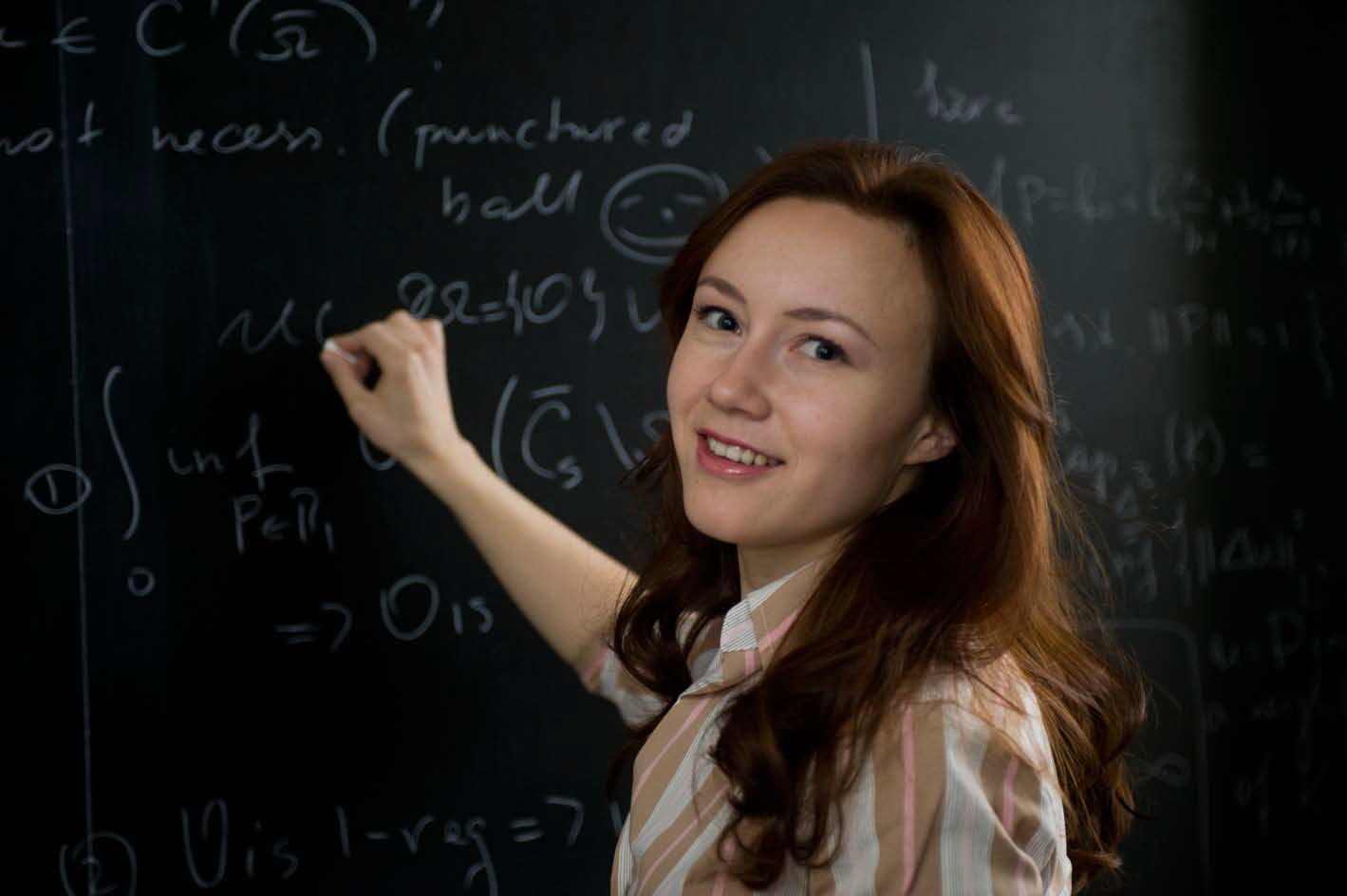
Position:
Professor of Mathematics,
ETH Zurich
McKnight Presidential Professor,
University of Minnesota
Address:
Department of Mathematics
ETH Zurich
Zentrum campus,
Ramistrasse 101,
8092 Zurich
School of Mathematics
University of Minnesota
127 Vincent Hall,
206 Church St. SE,
Minneapolis, MN 55455
Office:
HG G 63.2
Vincent Hall 510
Phone:
41-44-632-4169
1-612-624-4001
E-mail:
svitlana.mayboroda@math.ethz.ch
svitlana@math.umn.edu
|
 |
|
MENTORING: STUDENTS AND POSTDOCS
Postdoctoral Researchers:
- Vikram Giri , ETH Zurich, Fall 2023-present.
- Jaume de Dios Pont , ETH Zurich, Fall 2023-present.
- Laura Shou, University of Minnesota, Fall 2022-2023.
- Stefano Decio , University of Minnesota/ETH Zurich, Fall 2022-present.
- Tomas Merchan Rodriguez, University of Minnesota, Fall 2020-2022. Tomas obtained his PhD from Kent State University under the supervision of Benjamin Jaye and Fedor Nazarov. Starting in 2020, Tomas worked on the regularity of solutions as well as the Robin boundary value problem for elliptic operators on domains with low dimensional boundaries. In 2022, Tomas accepted a position as an Assistant Professor at Clayton State University.
- Shiwen Zhang, University of Minnesota, Fall 2019-August 2022. Shiwen Zhang obtained his PhD from the University of California, Irvine in 2016, under the supervision of Svetlana Jitomirskaya, and then worked as a postdoc at Michigan State University from 2016 to 2019, under the supervision of Alexander Volberg. From the Fall of 2019, he has started working under the supervision of Svitlana Mayboroda and Douglas Arnold on localization landscape theory. In particular, he worked on landscape law for eigenvalue approximation, Poisson-landscape equations etc. Shiwen is an Assistant Professor at UMass Lowell as of the Fall of 2022.
- Linhan Li, University of Minnesota, Fall 2019-July 2022. Linhan has obtained her Ph.D. degree from Brown University under the supervision of Jill Pipher. She joined the University of Minnesota as a Dunham Jackson Assistant Professor in August 2019 and worked under the supervision of Svitlana Mayboroda on properties of the Green function and elliptic measures for operators with nonsmooth coefficients. Linhan will join the University of Edinburgh as a Lecturer in the Fall of 2022.
- Guillermo Rey, University of Minnesota, Fall 2018-Spring 2019. Guillermo was a postdoctoral fellow at the University of Minnesota. His work focuses on localization of eigenfunctions and the behavior of harmonic measure on rough boundaries. His main research interests include harmonic analysis, geometric measure theory, and partial differential equations. Previously, he worked as a software engineer at Google, after completing his Ph.D. in mathematics at Michigan State University in 2015.
- Robert Viator, University of Minnesota and IMA, 2016-2017. Robert Viator was a postdoctoral research at the Institute for Mathematics and Applications. He has graduated from Louisiana State University under the supervision of Robert Lipton and, in addition to his duties at the IMA, worked on the localization landscape approach to Weyl law in periodic structures, under the supervision of Svitlana Mayboroda.
- Simon Bortz, University of Minnesota, September 2016-present. Simon Bortz has graduated from the University of Missouri, under the supervision of Steve Hofmann, in the Spring of 2016. He joined the University of Minnesota from the Fall of 2016, to work on the project partially funded by the NSF INSPIRE grant (see above). Specifically, Simon worked on Dirichlet, Neumann, and regularity problems in higher co-dimension, as well as layer potentials for the generalized Schr\"odinger operator. He is an acting assistant professor at the University of Washington as of the Fall of 2018.
- Joseph Feneuil, University of Minnesota, September 2015 - Spring 2018. Joseph Feneuil has graduated from the University of Grenoble, under the supervision of Emmanuel Russ. He joined the University of Minnesota as a Dunham Jackson postdoctoral researcher in the Fall of 2015 and worked under the supervision of Svitlana Mayboroda on analogues of harmonic measure in higher co-dimension. He is a research assistant professor at Temple University as of the Fall of 2018.
- Stephen Lewis, University of Minnesota, September 2014 - January 2015. Stephen Lewis has obtained his PhD from the University of Washington in 2014, under the supervision of Tatiana Toro, and has started working under the supervision of Svitlana Mayboroda and Douglas Arnold on localization of waves. He has left University of Minnesota in 2015 to work in industry.
- Blair Davey, University of Minnesota, 2013--2015. Blair has obtained her PhD degree from the University of Chicago with Carlos Kenig. She has started working with Vladimir Sverak on unique continuation for elliptic and parabolic equations and with Svitlana Mayboroda on boundary value problems for Schr\"odinger-type elliptic operators. In this direction, Blair (together with S. Mayboroda's graduate student, Jonathan Hill) has established pointwise bounds and regularity for fundamental solutions of general elliptic PDEs of Schr\"odinger type with bounded measurable coefficients, obtained the corresponding results for the Green function, and is currently working on the properties of the corresponding layer potentials. Blair is an assistant professor at CUNY as of the Fall of 2018.
- Ariel Barton, Purdue University and University of Minnesota, 2010--2013. Ariel has obtained her PhD degree from the University of Chicago under the supervision of Carlos Kenig, and was working on the higher order elliptic problems on Lipschitz domains and second order problems with rough coefficients (mentored by Svitlana Mayboroda). During her postdoctoral studies, Ariel has finished 5 research papers, 3 of them jointly with Svitlana Mayboroda, 1 expository (see the list of publications above), and 1 monograph, jointly with Svitlana Mayboroda, accepted to Memoirs of the AMS. Ariel then held a position at the University of Missouri. She continued working on the higher order elliptic operators, specifically, well-posedness problems for divergence form elliptic PDEs with bounded measurable coefficients, under the supervision of Steve Hofmann and Svitlana Mayboroda. During this time, she has finished 1 paper on boundedness of layer potentials for higher order PDEs (joint with S. Mayboroda and S. Hofmann), an expository paper on recent developments in higher order elliptic theory (joint with S. Mayboroda) and the work on the fundamental solutions in this context (by herself). Ariel is an assistant professor at the University of Arkansas, Fayetteville as of the Fall of 2018.
Graduate
Students:
- Aaron Moser, ETH Zurich.
- Cole Jeznach, ETH Zurich, is a graduate student supervised jointly with Max Engelstein. He is working on the study of elliptic measure outside of sets with low dimension.
- Zanbing Dai, University of Minnesota, graduated in Spring 2023. Zanbing studied the regularity problem for second order elliptic operator in higher co-dimension.
- Bruno
Poggi, University of Minnesota, graduated in Spring 2021 as a doctoral dissertation fellow, his thesis Boundary value problems for second-order elliptic equations and related topics having garnered the 2021 Outstanding Thesis Award in the Department of Mathematics. He is currently a postdoctoral investigator at the Universitat Autonoma de Barcelona, working with Xavi Tolsa.
- Jonathan Hill, University of Minnesota, graduated in Spring 2017. Jonathan worked on the properties of the Green function for elliptic operators with bounded measurable coefficients. He has showed that in the case of an elliptic operator with $t$-independent coefficients the Green potential exhibits appropriate mapping properties in weak-$L^p$ spaces (and this is sharp) and considered also more general operators and systems. In particular, he worked with Blair Davey on well-posedness of boundary problems for generalized Schroedinger operators.
- Koushik
Ramachandran, Purdue University, graduated in
May 2014. Koushik was working on asymptotics of harmonic
functions in rough paraboloid-shaped domains (supervised by
Svitlana Mayboroda jointly with Alexandre Eremenko). He has
published the results of his dissertation and has moved on
to a postdoctoral position at the Indian Statistical
Institute (ISI) at Bangalore, India.
- Eli Johnson, University of Minnesota, has worked on the boundary regularity for fractional Laplacian under the supervision of Svitlana Mayboroda. He is now a graduate student at the University of Washington.
Undergraduate Research:
The resulting publication (in Contemporary Mathematics) can be found hereBrandon's talk on the results of our present project at the SIAM Computational Science and Engineering Student Conference at Purdue in 2011 has been awarded.
the Best Undergraduate Speaker Award
Brandon is now a graduate student at the University of Michigan
- Landon Lehman
has been investigating the dependence of Anderson
localization on the magnitude of disorder under the
supervision of me and Ariel Barton
Landon is a clinical assistant professor of physics at SUNY as of the Fall of 2018.
- Ye Wang, University of Minnesota, 2013, has successfully completed a UROP (Undergraduate Research Opportunities Program) project on Localization of vibrations and conformal mappings.
- Yaowen Gu, University of Minnesota, 2012, has successfully completed a Senior Project on the Harmonic measure and Brownian motion.
- Levi Walls, University of Minnesota, 2016, has been
studying boundary value problems for elliptic equations,
spectral theory, and spherical harmonics.
- Joseph Pate, University of Minnesota, 2016-2017,
worked under the supervision of Svitlana Mayboroda on the
properties of the landscape function for the Neumann
problem, in concert with the localization of Neumann
eigenfunctions. He has received the UROP (Undergraduate
Research Opportunities Program) award and was supported in
part by the REU project within S. Mayboroda's CAREER grant.
TEACHING:
- Real Analysis, graduate, Fall 2014, University of Minnesota.
- Theory of Partial Differential Equations -- II, graduate, Spring 2014, University of Minnesota.
- Linear Algebra and Differential Equations, undergraduate,
Spring 2013, University of Minnesota.
- Introduction to Distributions, graduate, reading course,
Summer 2011, Purdue University.
- Partial Differential Equations, Spring 2011, Purdue University.
- Ordinary Differential Equations, Fall 2010, Purdue University.
- Ordinary Differential Equations, Fall 2009, Purdue University.
- Differential Equations and Partial Differential Equations for Engineering and the Sciences, Fall 2008, Purdue University.
- Accelerated Calculus with Analytic Geometry II, Winter 2008, The Ohio State University.
- Real Analysis I-III, Fall 2006, Winter 2007, Spring 2007, Spring 2008, The Ohio State University
- Mathematical Analysis for Business II, Spring 2006, The Ohio State University
- Calculus and Analytic Geometry I, Winter 2006, The Ohio State University
- Analytic Geometry and Calculus I, Fall 2004, University of Missouri-Columbia
- Calculus II, Fall 2003, University of Missouri-Columbia
- Elements of Calculus, Winter 2003, Winter 2004, Winter 2005, University of Missouri-Columbia
- College Algebra for Calculus Bound Students, Fall 2002, University of Missouri-Columbia