Faraday waves

Parametrically driven surface waves (also known as Faraday waves) can be excited on the free surface of a fluid layer that is periodically vibrated in the direction normal to the surface at rest if the amplitude of the driving acceleration is large enough to overcome the dissipative effect of fluid viscosity. 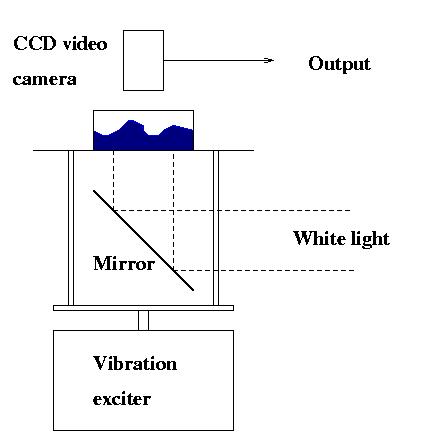This is a schematic of the experimental setup. The fluid is set on top of a vibration exciter, light shined though it, and the resulting image is recorded by a camera.

An excellent introduction to Faraday waves is the online presentation by Jerry Gollub, which is one of the plenary talks given at the APS Centennial Meeting.

A great deal of our research effort has been devoted to the study of parametrically driven surface waves in the large aspect ratio limit. Active modes above threshold are only weakly damped (or not damped at all in the limit of an inviscid fluid), so that the governing equations are close to being purely Hamiltonian in nature. This is in contrast to other widely studied pattern forming systems in which overdamped motion is dominant. Hence an important question concerns the mechanism of nonlinear wave saturation, and with it the selected pattern above onset.

The experimental phenomenology concerning pattern selection above onset can be summarized as follows. At high viscous dissipation (a fluid of large viscosity and/or a low driving frequency), the observed wave pattern above threshold consists of parallel stripes [W.S. Edwards and S. Fauve, J. Fluid Mech. 278 , 123 (1994)]. For lower dissipation, patterns of square symmetry (combinations of two perpendicular plane waves) are observed in the capillary regime of large frequencies [.B. Ezerskii, M.I. Rabinovich, V.P. Reutov, and I.M. Starobinets Sov. Phys. JETP 64, 1228 (1986), N.B. Tufillaro, R. Ramshankar, and J.P. Gollub Phys. Rev. Lett. 62, 422 (1989), B. Christiansen, P. Alstrom, and M.T. Levinsen Phys. Rev. Lett. 68, 2157 (1992)]. At low frequencies (the mixed gravity-capillary regime), higher symmetry patterns have been observed: hexagonal [A. Kudrolli and J.P. Gollub Physica D 97, 133 (1996)], and eight- and ten-fold quasi-periodic patterns [D. Binks and M.-T. Westra and W. van de Water Phys. Rev. Lett. 79, 5010 (1997)].

These indings are summarized in the figure below in terms of the frequency of the driving acceleration and the viscosity of the working fluid.

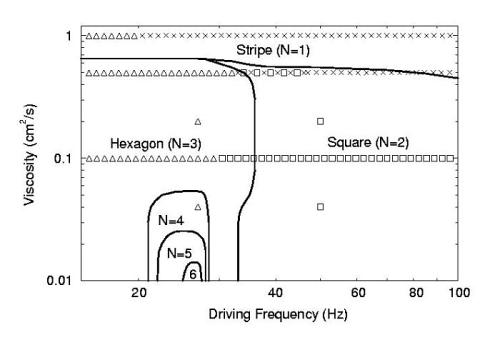
The symbols are the results of an experimental survey by Kudrolli and Gollub [A. Kudrolli and J.P. Gollub Physica D 97, 133 (1996)] and the lines delimit the regions of stability of the patterns of the indicated symmetry [P. Chen and J. Viñals, Phys. Rev. Lett. 79, 2670 (1997)].

A salient feature of this diagram is the existence of a region of parameters in which quasiperiodic patterns are predicted to be stationary (an example is shown here). The regions denoted by N=4, N=5 and N=6 corresponds to eight-fold, ten-fold and twelve-fold quasi-patterns. These patterns are the analog of a quasi-crystal in solid state physics. Patterns with these symmetries have been observed experimentally in the regions shown in the figure [D. Binks and W. van de Water, Phys. Rev. Lett. 78, 4043 (1997), D. Binks and M.-T. Westra and W. van de Water, Phys. Rev. Lett. 79, 5010 (1997).

Research currently under way aims at the study of this system at a finite distance from threshold. It is now known that whereas the evolution of the wave pattern near onset is variational, the region in parameter space exhibiting variational behavior is small in most fluids (and vanishes with the viscous damping parameter). Therefore nonvariational corrections are anticipated to be large even relatively near onset, and to play a prominent role in secondary instabilities of the base stationary wave pattern, and on the transition to spatio temporal chaos.